voidmax's blog

Tinkoff Internship Warmup Round 2018 and Codeforces Round #475

By voidmax, 7 years ago, translation, In English

Tinkoff Internship Warmup Round 2018 and Codeforces Round #475 will start at 17 April 2018 17:05,

Thanks to Vladislav winger Isenbaev, Alex AlexFetisov Fetisov, Ildar 300iq Gainullin, Egor Egor.Lifar Lifar, Philip grphil Gribov and Gleb Glebodin Lobanov for testing my problems.

Special thanks to Grigory vintage_Vlad_Makeev Reznikov and Nikolay KAN Kalinin for coordinating throughout the round and Mike MikeMirzayanov Mirzayanov for remarkable systems Codeforces and polygon.

Round is rated for both divisions. There are 5 problems, and 2 hours to solve them. The points distribution will be updated later.

Good luck and Have fun!

UPD The points distribution for both divisions: 500 — 1000 — 1500 — 2000 — 2500

UPD Congratulations to the winners!

Div 1:

Div 2:

UPD >>> Editorial <<<

  • Vote: I like it
  • +280
  • Vote: I do not like it

Comments Comments (184)
| Write comment?
»
7 years ago, # |
← Rev. 2   Vote: I like it -122 Vote: I do not like it

Wish high ratings everyone

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +124 Vote: I do not like it

    Please stop all these comments about Wish high rating and is it rated and short problem statements.

    Every one wishes that. So it is not important to write these comments. Keep comment section clear for more important things.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it +17 Vote: I do not like it

      If everyone was high rated no one would be high rated :o

      → Reply
»
7 years ago, # |
  Vote: I like it +9 Vote: I do not like it

Why isn't there an English version of the blog?

→ Reply
»
7 years ago, # |
  Vote: I like it -143 Vote: I do not like it

Is it rated?

→ Reply
»
7 years ago, # |
  Vote: I like it +26 Vote: I do not like it

I got worried when the registration was only privet :D

→ Reply
»
7 years ago, # |
  Vote: I like it +53 Vote: I do not like it

2 previous Tinkoff rounds

  1. Tinkoff Challenge — Final Round
  2. Tinkoff Challenge — Elimination Round
→ Reply
»
7 years ago, # |
  Vote: I like it -73 Vote: I do not like it

Is It Rated?

→ Reply
»
7 years ago, # |
  Vote: I like it +21 Vote: I do not like it

thanks, finally it's 5 problems

→ Reply
»
7 years ago, # |
  Vote: I like it -63 Vote: I do not like it

The points distribution will be updated later.

This sentence is wrong, correct one is :

The points distribution will not be updated before contest.

→ Reply
»
7 years ago, # |
  Vote: I like it +5 Vote: I do not like it

Why I can't register for the contest now???

→ Reply
»
7 years ago, # |
  Vote: I like it -28 Vote: I do not like it
The comment removed because of Codeforces rules violation
→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

What was Div2 B?

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 3   Vote: I like it 0 Vote: I do not like it

    if C > B, it is better to leave message unread as long as possible. So read the message on time T

    C = B, time doesn't matter

    C < B, it is better to read message as fast as possible. So read the message on t_i

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      why this right ?

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
        ← Rev. 2   Vote: I like it +1 Vote: I do not like it

        If you read the message x seconds after receiving it, you will receive A + (C - B) * x money.

        → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Any Idea of pretest 7 for Div2C?

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Please!! What's the hack data for B?

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +38 Vote: I do not like it

Is it just me or B was much more difficult than usual?

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it +102 Vote: I do not like it

#easy

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Too much maths for Div2

→ Reply
»
7 years ago, # |
  Vote: I like it +28 Vote: I do not like it

Any idea of pretest 9 in DIV2C and pretest 7 in DIV2D?

→ Reply
»
7 years ago, # |
  Vote: I like it +8 Vote: I do not like it

how to solve problem D in div2 ? so sad of wr7

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    x2

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    x3

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    5 0 1 2 2 4

    My initial code failed this test and it was getting WA in test 7.

    I think that the answer is to remove the deepest node with even degree, because none of its children have even degree so they can't be removed unless this node is removed first.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      I think you can remove any such node that all the remaining trees would have odd sizes. This is easily done using BFS or a set(), since each removal only changes the "parity" of adjacent nodes.

      → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

oh..the contest is over...maybe it is too hard for me.....

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In Div2 D isn't it always possible to destroy the tree by removing the leaf vertices and then proceeding upwards in this fashion?

The leaf nodes will always have a degree zero which is even right ?

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it -9 Vote: I do not like it

Can anyone explain how can this O(n) solution 37407108 for Div2A pass when I tried to hack it with test case n = 10^9 ? voidmax

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    Because C++ has optimizer. This programm works in O(1).

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Oh. This trivial information costed me 50 points penalty.

      → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Compiler optimized it to n/2

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Compiler optimization?

    → Reply
»
7 years ago, # |
← Rev. 3   Vote: I like it +22 Vote: I do not like it

Regarding "Destroying a tree", it matters the order in which the vertices are selected. For example, consider this test case:

5
0 1 1 2 3

If you start from vertex 1, then it's impossible to destroy the tree, but if you start with vertex 2, then the order "2 4 3 1 5" is valid.

Unfortunately, I couldn't make it up to find out a strategy that always brings the correct result and maybe that's why I failed pretest 7.

Kudos to voidmax for the interesting problemset!

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +6 Vote: I do not like it

    Root the tree from a random vertex. It's always optimal to destroy a vertex with largest depth (and even degree of course).

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Can you explain why?

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
        ← Rev. 2   Vote: I like it +6 Vote: I do not like it

        This is probably not a proof, it is just my thinking during the contest

        Suppose that you have two vertex with even degree (one is parent of other).

        If you remove the parent, the child will be affected, you will need to remove some child to have even degree again... It's kinda hard to check this from parent to child (root to leaf).

        Try to go in the opposite way: from leaf to root.

        You have a leaf (obviously odd degree), how can you remove it? You need to remove it's parent... If the parent is odd, then you need to keep checking the parent until you reach a vertex with even degree. Now you remove it.

        Then you have just disconnected the tree, the new tree should be solvable, otherwise "NO"

        → Reply
      • »
        »
        »
        »
        4 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Hi Yash, did you figure out a proof. I really want to know how this works but I can't prove it. The comment linked by the author below also doesn't help :/

        → Reply
        • »
          »
          »
          »
          »
          4 years ago, # ^ |
          ← Rev. 4   Vote: I like it 0 Vote: I do not like it

          PROBLEM D GREEDY PROOF

          OK I figured it out for anyone in the future who falls in trouble:

          1. Removal of the deepest even-degree node causes further removal of even number of nodes in its subtree (easy proof by induction)
          1. This means that odd-even=odd which means that the number of nodes remaining in the subtree is odd. Which means again, by initial lemma, that there exists atleast one node with even degree.
          → Reply
»
7 years ago, # |
  Vote: I like it +9 Vote: I do not like it

wake me up when systests start

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

What is pretest 15 in Div1 C?

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Why this o(n) sollution passes system testing? 37405016

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +6 Vote: I do not like it

    Because C++ has optimizer. It easily optimizes this sort of for, so programm works in O(1).

    → Reply
»
7 years ago, # |
  Vote: I like it +90 Vote: I do not like it

Please, just run systests faster and let us go to sleep, we have rehershal tommorow :/

→ Reply
»
7 years ago, # |
  Vote: I like it +14 Vote: I do not like it

What is correct solution to B anyway? I know that:

  • If a tree has even number of vertices, the answer is 'NO'.
  • Otherwise, there is always at least a even-degree vertex. However, I don't know if it is true that there is always at least a even-degree vertex that seperate the tree into smaller component that has odd number of vertices (If it is true, just choose this vertices and solve the subproblem). I couldn't find a counterexample so I bet my luck in it, but failed miserably.
→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 3   Vote: I like it +30 Vote: I do not like it

    There will definitely be a vertex with even degree breaking the tree into odd components. We can first remove all even sized subtrees of the root. Once all even sized subtrees have been visited, print current vertex and then visit odd sized subtrees. In this method, we are considering either odd sized trees with no parent edge, or even sized trees with a parent edge, and you can prove using induction that this works :

    void dfs(int s = 1, int p = 0){
	for(int v : con[s]) if(v != p && subtree[v] %2 == 0) dfs(v, s);
	printf("%d\n", s);
	for(int v : con[s]) if(v != p && subtree[v] % 2 == 1) dfs(v, s);
}
    → Reply
    • »
      »
      »
      4 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it 
      "There will definitely be a vertex with even degree breaking the tree into odd components."

      That's what he asked to be proved.

      → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +34 Vote: I do not like it

    You can remove the vertices greedily by its heights: remove the ones with greater height first.

    If you are removing a vertex V, its subtree has no vertex X ≠ V with odd degree, otherwise it would be removed before V. The children of V will now have even degrees, since just one edge is removed from them, and you can apply the same idea to them, since their subtrees have no nodes with odd degree beside them.

    So, all components that were on V's subtree are good to go; you just need to prove that the upper component is good to go too. That's easy: since the number of edges in V's subtree is even, then the parity of removed edges of the upper component did not change, which implies that there is another even-degree vertex to be removed.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +6 Vote: I do not like it

      Thanks for the explaination. Feel sad for not figuring this out in the contest...

      → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Could you explain why answer is No when tree has even number of vertices?

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +12 Vote: I do not like it

      Even number of vertices have odd number edges .And you always delete some even number of edges

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        What a simple idea it was. Deleting a vertex will separate trees, that thought confused me. thanks.

        → Reply
»
7 years ago, # |
← Rev. 3   Vote: I like it 0 Vote: I do not like it

Could anyone please drop a couple of hints on Div2C? (Div1A)
How to approach this kind of problems?

Update:
Oh, I got it now.
Thank you, aangairbender.

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +25 Vote: I do not like it

    You can calculate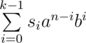 (we will call it T) in O(k * log(k)) time complexity. It will be the sum of one period.

    Two consecutive periods are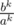 times different — we can call that value Z.

    The number of periods will be (n + 1) / k = Q.

    Therefore, the final answer should be: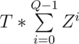 , or .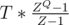

    All of these can be calculated with modulo addition/multiplication/inverse.

    Update: Just see the update of your comment. Nevermind, hope you can find something useful in mine ;)

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +4 Vote: I do not like it

      Thank you!
      I indeed find your comment useful.
      Specifically, it did not come to my mind during the contest that consecutive periods differ by (ak / bk) times.

      → Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +14 Vote: I do not like it

    Let Sum[0, k) be the summation of first K terms of that series.

    Now you can observe that Sum[k, 2 * k) = (bk / ak) * Sum[0, k)

    Similarly, You can divide the whole series in (n + 1) / k terms which is a G.P with common ratio (bk / ak) and then use the formula for the sum of geometric progression (don't forget the case when common ratio of this G.P is 1).

    → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Can anyone tell me if this solution for Div2.D is correct? I came upon it too late in the contest and didn't have time to implement it. So, here it goes:

Lets start at the leaves, it is obvious that their parent will have to be destroyed before them.

Now let's go 1 level up on the tree, if a parent of a leaf has even degree, then for sure its parent will have to be after before it, otherwise it wouldn't be possible to destroy it.

If it has an odd degree, then it will have to be destroyed before it. Now, lets substract the number of sons that will have to be clicked before their parent from the parent degree and continue doing the same procedure, going up the tree.

Lets make a directed graph, that has edges (u,v) for every u and v such that they are adjacent in the tree and u has to be clicked before v.

Do a topological sort on this graph and start clicking vertices in order, if at some step we have to click a vertex with odd degree, there is no solution. Otherwise, simply clicking in order will produce a solution.

→ Reply
»
7 years ago, # |
  Vote: I like it +8 Vote: I do not like it

Actually I will kill myself. I used f***ing std:map< string > and I didn't realize it is |S|·log.

P.S. I read comment it is always optimal to destroy vertex with the largest depth, why it is not good to destroy vertex with largest id ?

→ Reply
  • »
    »
    7 years ago, # ^ |
    ← Rev. 2   Vote: I like it +35 Vote: I do not like it

    Because ids are arbitrary. You can relabel the nodes in any way that you want. (as long as you output them with their original labels)

    Also don't kill yourself.

    → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

I am probably the only person who tried to solve Problem B using Dynamic Programming. I am sooooo stupid.

→ Reply
»
7 years ago, # |
  Vote: I like it +10 Vote: I do not like it

"Oh, they changed the mod from 1e9+7, that must mean it's not prime."

Why would you do this to us

→ Reply
»
7 years ago, # |
  Vote: I like it +75 Vote: I do not like it

When you get wrong answer on E after system testing...

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

help please with this submission of DIV 2 C: http://mirror.codeforces.com/contest/964/submission/37413366 upd: solved, thanks voidmax

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can anyone explain, why it is always optimal to remove nodes from deeper level in div2 D?

→ Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

1) Evil 2) Very Evil 3) Not putting any pretest cases where C-B > 1 for B :3

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    LOL I was hacked perhaps by that exact case :D

    Well, thinking about it, being hacked seems to be fortunate :)

    → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can someone help me？My code of div1.A is similar to others accepted submissions but why I got Wrong Answer on test9？

→ Reply
»
7 years ago, # |
  Vote: I like it +21 Vote: I do not like it

I normally have something to complain about the rounds (even though I never comment) but this round's problems were great.

→ Reply
»
7 years ago, # |
← Rev. 6   Vote: I like it +33 Vote: I do not like it

Now failed systest on A too... Why not allow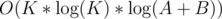 solution...

It seemed that I still have a lot of thing to do if I want a slot in ACM-ICPC WF

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +18 Vote: I do not like it

    Revision history of the comment is me irl

    → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    If I had to guess, I'd say it's not a problem of time complexity, but of correctness.

    In your submission, you write int t =k*n/2, but the multiplication can exceed the limits of the int type, causing undefined behavior. What I'm guessing is that at some point this t becomes negative and since you passed it as an exponent to your power function, it will cause an infinite loop.

    Just a hunch though, I'm not at my laptop right now so I can't test :)

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      t will never exceed n in the problem statement.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Why? Which part of the problem statement leads you to believe that?

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it +5 Vote: I do not like it

          I called the function in this manner:

          Calc(..., ..., k, (N+1)/k);

          So t will never exceed N/2 (let N be the 'n' in the problem statement so it won't be ambigious).

          → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
          ← Rev. 2   Vote: I like it 0 Vote: I do not like it

          I got accepted after improving the complexity to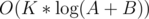 , and I didn't change the Calc function in my code.

          37415485

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            You can calculate first block in complexity O(K + log(A + B). First calculating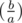 , so you can calculate all degrees up to .

            → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

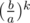What's wrong with my solution ofr div2 C? http://mirror.codeforces.com/contest/964/submission/37415514

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Editorial?

→ Reply
»
7 years ago, # |
  Vote: I like it +3 Vote: I do not like it

The feeling of becoming Expert.

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I think the time limit for Div1 A/ Div2 C should have been 2 seconds considering order of 10^6 modulo operations.

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

But is that true, that with given constraints (k <  = 105)(b / a)k = 1 implies (b / a) = 1?

→ Reply
»
7 years ago, # |
  Vote: I like it +19 Vote: I do not like it

Jesus! I can't believe my bogus solutions for B and D passed System Tests !!!!!!

My solution for B: Maintain a set with all nodes with even degree ordered by depth first (distance to root). At each step, remove the deepest node (farthest from the root) and update degrees accordingly, removing or adding to the set as necessary.

My solution for D: Perform Suffix Array on S. Then for each query (t, k), all occurences of t in S will form a contiguous segment in the Suffix Array. Let the suffix array be SA, and suppose that the subarray for a given query in it is (l, r), then we need to find a set X of k indices i1, i2, ..., ik from the range (l, r) such that max(SA[i]) - min(SA[i]) is minimized (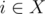). I did that by pushing all SA[i] with l ≤ i ≤ r to a vector, then sorting the vector and checking all values of vi - vi - k + 1 for all i ≥ {k - 1}. I was certain this approach would get TLE in a very early test case. I can't believe such a thing passed systests....... but I'm really happy it did! :)

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +23 Vote: I do not like it

    Your solution for D works in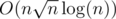 . Let's consider all strings of the same length. The total number of their occurrences in s is O(n), because at each position there can be at most one string. The number of defferent lengths is . So the number of all occurences is 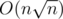. You can also get rid of additional 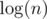if you use Aho-Corasick instead of suffix array.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thanks a lot for the insight!

      I will certainly look into that algorithm :)

      → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    i can prove your solution for B and it's true :))

    so tests are okay ...

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
      ← Rev. 2   Vote: I like it +5 Vote: I do not like it

      Yeah, I have no doubt tests are okay. It's just that I didn't prove it myself, I just thought "I guess this approach will work" and decided to blindly submit.

      The same for D, I didn't put too much thought into how many different lengths and matches could occur and didnt' do the math. I just coded the first thing that came to my head and submitted.

      That's why I didn't expect either of them to pass. Seeing my rating increase and ranking 50+ was a very pleasant surprise :)

      → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

My solution for B div1:

Always process the child nodes first before their parent (like a topological sorting where the directed edges go from the nodes to their parent). Initially start with the leaf nodes in the queue of the nodes to be processed. When processing a node, if its degree is even, delete the whole subtree rooted at it, and decrease the degree of its parent by 1. And after processing the node, look at its parent, if this parent has its children all processed then push this parent to the queue. At the end, you succeed if you have deleted the whole tree.

This idea is based on the fact that the information you start with is that the leaf nodes can't be removed unless their parents are removed. And if you processed the whole subtree under some parent and this parent still can't be removed you have to remove its parent, and so on. If you reached the root and couldn't remove it, so it is impossible to remove all nodes.

→ Reply
»
7 years ago, # |
  Vote: I like it +27 Vote: I do not like it

I see many people have provided greedy solutions for Div1B/Div2D. Here's my DP on tree solution (which ACed) for those interested:

First, observe that for any vertex u, having parent v, you can destroy the subtree of u either entirely before destroying vertex v or entirely after destroying vertex v. So, let's classify our vertices into two types: 'before' vertex — a vertex whose subtree is destroyed before destroying it's parent and 'after' vertex — a vertex whose subtree is destroyed after destroying it's parent.

Now, identifying vertices is easy. First, note that all leaves are 'after' vertices. They can only be deleted after their parent is deleted. Now, observe that a vertex is a 'after' vertex if and only if it has even number of children who are 'after' vertices, otherwise it is a 'before' vertex.

So, all vertices can be classified into 'after' and 'before' with a single DFS. The answer to our question is YES if the root is an 'after' vertex otherwise it is NO. Printing the solution is also easy, for printing the solution of the subtree of vertex u, print the solutions of all it's children who are 'before' vertices, then print u, then print the solutions of all 'after' vertices.

Here's my code: Destruction of a Tree

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

How to solve div1 E?

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +8 Vote: I do not like it

    Please, wait for editorial, i'm preparing it now.

    → Reply
»
7 years ago, # |
  Vote: I like it +29 Vote: I do not like it

Still waiting for the editorial...

→ Reply
»
7 years ago, # |
  Vote: I like it +8 Vote: I do not like it

On div 1 Problem D test 22. The n is 80445 by assert, and the kind of lengths of mi is at least 325 by assert too. So Sum of length of all strings in input is at least 133420. That's illegal to the tips of the subject.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +18 Vote: I do not like it

    There really is a problem but I don't think that would be. The problem is that the problem mentioned "Sum of length of all strings in input doesn't exceed 10^5", the total length of query is less than or equal to 10^5, but including the string s, the total length is greater than 10^5. But I don't think it caused any trouble.

    → Reply
»
7 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

WHY got TLE in Div1 D using a Aho-Corasick automaton to brute force maintain the occurrences of each query strings?

I thought the time complexity is O(n sqrt(n))

my code here:37415123

→ Reply
»
7 years ago, # |
  Vote: I like it +7 Vote: I do not like it

So when can we see the tutorial of the contest? I really need it. thx!

→ Reply
»
7 years ago, # |
  Vote: I like it +35 Vote: I do not like it

Thanks for the round voidmax, great problems! (except div1 D)

→ Reply
»
7 years ago, # |
  Vote: I like it +42 Vote: I do not like it

Since there's no editorial, here are some solutions:

  • B: No clever tricks, just tree DP — is it possible to delete the subtree of v if the parent of v is deleted before v / after v? If we determine which sons of v should be deleted before v for both of these cases, the order of deleted vertices can be computed recursively (to delete the subtree of v, delete subtrees of sons deleted before v, delete v, delete subtrees of remaining sons). For the tree DP, if v has a son that can't be deleted in either case, the answer is no for both; if it has a son that can be deleted in both cases, the answer is yes for both, and otherwise, we know exactly which sons should be deleted before/after v.

  • C: If the answer is non-zero, the problem can be formulated this way: we have a complete edge-weighted bipartite graph (vertices are widths and heights of rectangles, edges are rectangles, weights are ci); count the number of ways to assign integer weights to the vertices in such a way that the weight of each edge is the product of weights of its endpoints. This can be solved independently for each prime factor — we're adding exponents instead of multiplying integers, everything is determined uniquely if we fix one exponent, and since these exponents are small, we can try all possibilities for one of them and check by bruteforce if it actually leads to a valid assignment. We only need to deal with prime factors of w.l.o.g. c1; afterwards, we're left with a graph that has c1 = 1, and need to check if the only possible assignment in this graph is valid. Time complexity: .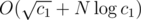

  • D: If we know all positions where a query string occurs in s, the answer for this query can be easily computed in linear time with no additional overhead. Actually, there are sufficiently few of these positions, so we can find them all. For a query string with length greater than sqrt (let's say 100), we can find them by KMP with overhead O(|s|); there are only sqrt of these strings. All query strings with length at most sqrt can be stuffed into a trie. Now, for each suffix of s, we can find a path in the trie corresponding to this suffix (with length at most sqrt, since that's the depth of the trie), and all query strings that end in vertices on this path occur on the position corresponding to this suffix. Time complexity: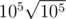 . You can get MLE or TLE, watch out for your trie implementation, try to put smaller strings in it or use a hashmap instead.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Problem B has a greedy approach too -> here

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      That's the approach with clever tricks.

      → Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it +10 Vote: I do not like it

    Solving D with only Aho-Corasick is also possible. Just put all query strings in the trie and compute the suffix links. Then iterate over the text characterwise and record all occurences.

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it -13 Vote: I do not like it

      Aho-Corasick is solid overkill compared to KMP and tries. Yes, this is a deterministic memory-efficient solution, but I like to avoid Aho-Corasick whenever possible.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        You seem to not understand Aho-Corasick if you think that KMP and trie is simpler. Because Aho-Corasick is literally KMP and trie. It even can be written as combination of those.

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it -26 Vote: I do not like it

          Ok, wise guy, answer this: in what order do you compute backlinks and where in KMP or trie do you need to think about it?

          → Reply
          • »
            »
            »
            »
            »
            »
            7 years ago, # ^ |
              Vote: I like it +5 Vote: I do not like it

            In order of length increasing, same for kmp.

            → Reply
            • »
              »
              »
              »
              »
              »
              »
              7 years ago, # ^ |
                Vote: I like it -26 Vote: I do not like it

              In KMP, it's also in DFS order, or in the order in which vertices were added. So you didn't answer the second part of my question: where in KMP do you need to think about which order (out of at least 3 possibilities) it should be?

              → Reply
              • »
                »
                »
                »
                »
                »
                »
                »
                7 years ago, # ^ |
                  Vote: I like it +28 Vote: I do not like it

                You don't need to think of it in both Kmp and Aho-Corasick if you have proper images of how it works in your head. Both algo proven by induction over length, so you use order of lengthes in your implementation. That's just ridiculuous that you think that it is hard to choose between dfs and bfs in such a case.

                → Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Can any one please help me about my solution of Problem B I use a O(n) algorithm but I get TLE.. http://mirror.codeforces.com/contest/963/submission/37431208

→ Reply
»
7 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Why is my solution for Div.2 C computing 1 as the answer for TC 7? LINK

Thank you in advance.

→ Reply
  • »
    »
    7 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    While addition, subtraction and multiplication are straightforward in modular arithmetic

    ( (a op b) % mod = ((a % mod) op (b % mod)) % mod, where op is one of +,-,* )

    the same cannot be said about division:

    (a / b) % mod != ((a % mod) / (b % mod)) % mod. For instance, take (8/2) % 5.

    To do division in modular arithmetic, you multiply the numerator with the modular inverse of the denominator. A modular inverse for number a under the modulo n is such a number b that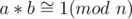 . This number b exists if and only if gcd(a, n) = 1. By Euler's theorem, we can conclude that b = aφ (n) - 1. You can read more about it online:

    Wikipedia

    → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it +3 Vote: I do not like it

      1e9 + 9 is the prime number so you can use Fermat's little theorem.

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        That is correct and is often what you use for solving tasks. I was just trying to offer a more general answer.

        → Reply
    • »
      »
      »
      7 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      a·b = 1

      b = ap - 2

      → Reply
      • »
        »
        »
        »
        7 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Out of curiosity, how will the following statement result in an overflow:

        (a / b) % m

        → Reply
        • »
          »
          »
          »
          »
          7 years ago, # ^ |
            Vote: I like it +13 Vote: I do not like it

          There's no overflow. The fact that division doesn't work in modular arithmetic doesn't have anything to do with a programming limitation such as integer variables having max values and overflowing. It just doesn't work mathematically.

          → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

hey, if someone could explain please why is the total weight of split of 8 equal 5? At 964A ... I mean, i found 4 of its splits but i can't find the fifth ... Thank you!

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    2,2,2,2

    2,2,2,1,1

    2,2,1,1,1,1

    2,1,1,1,1,1,1

    1,1,1,1,1,1,1,1

    → Reply