I'v tried to solve this problem from 4 or 5 days, but the only solution that I'v wrote finish running in 84 seconds using Segmented Sieve.
So is there any hints or resources to start working on the correct solution?
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
I'v tried to solve this problem from 4 or 5 days, but the only solution that I'v wrote finish running in 84 seconds using Segmented Sieve.
So is there any hints or resources to start working on the correct solution?
| Name |
|---|



You don't actually need to find all primes to cimpute the sum. E.g.here is a description of an approach, that only takes O(n^0.75) time. Link
Thank you for the link, but can you explain the method used? because I don't understand it.
What exactly didn't you understand? The only method used here is DP.
They just define a function that does a bit more than just a summation of the primes. S(v, p) is the sum of all numbers between 2 and v which are still in the sieve if you remove all multiples of all primes ≤ p. Every non-prime number below n has a factor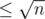 , so the answer to the problem is
, so the answer to the problem is 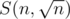 .
.
And for this function it is not too hard to come up with a recursive definition. If you don't understand it, just try it with a few numbers. E.g. for S(25, 3), and see what numbers they sum up, and what numbers you sum up with S(25, 3), and which numbers with 3 * S(8, 2) and 3 * S(2, 2).
Implementation was not described in the link. But I assume that a top-down DP approach is fast enough.