Hello,
It's my first Blog post and I decided to dedicate it to CROC-MBTU 2012, Elimination Round. I tried to do my best and explain ideas completely. Bear in mind that solutions aren't unique and they're only my ideas. At the end of each explanation, there exists a link to C++ implementation of problem. I hope this editorial will be useful. Any constructive criticism is appreciated. Please report any bug and/or mistake you encounter here in comments.
A. System Administrator
Let's define following variables:
AReached : Number of packets that reached A.
ALost : Number of packets which didn't reach A.
BReached : Number of packets that reached B.
BLost : Number of packets which didn't reach B.
We iterate over input and update each variable accordingly. Now answer for server A is LIVE if and only if AReached ≥ ALost otherwise it's DEAD. Also answer for server B is LIVE if and only if BReached ≥ BLost otherwise it's DEAD.
Implementation: C++
B. Internet Address
Problem guarantees that there exists an Internet resource address from which we can obtain our input. At first, let's find Protocol of address. It's sufficient to only check first letter of input, if it's h then protocol is http otherwise, it's ftp. Now, let's find position of .ru. We can iterate over our string from right to left and greedily choose the first occurrence of .ru as TLD. Now the rest of Internet address can be obtained easily as we have positions of Protocol and TLD. Just note that we should check whether < context > is present after .ru or not. Also picking .ru greedily from left to right fails following testcase, hence it's incorrect.
Input: httpruru
Incorrect output: http://.ru/ru
Correct output: http://ru.ru
Implementation: C++
C. Game with Coins
First note that if n ≤ 2 or 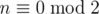 then answer is - 1. It's because of the following 2 facts:
then answer is - 1. It's because of the following 2 facts:
1. 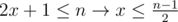 and
and 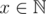 so n ≥ 3 otherwise x won't be a natural number.
so n ≥ 3 otherwise x won't be a natural number.
2. If 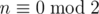 then n = 2k and
then n = 2k and 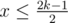 which means x ≤ k - 1 hence 2x + 1 ≤ 2k - 1 so there doesn't exist a x such that it satisfies problem's conditions and can be used to reduce a[n]
which means x ≤ k - 1 hence 2x + 1 ≤ 2k - 1 so there doesn't exist a x such that it satisfies problem's conditions and can be used to reduce a[n]
In other situations, there always exists a sequence which can finish the game. We now propose a greedy algorithm and then prove it's correctness.
Algorithm: Iterate from n to 2. Suppose that you're in position i. If 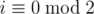 then take
then take 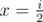 otherwise, take
otherwise, take 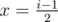 and execute operations with obtained x as long as a[i] > 0 and increase ans for each execution. At the end, increase ans by a[1] and output it. Remember to check if an element you're going to decrease by 1 is positive beforehand.
and execute operations with obtained x as long as a[i] > 0 and increase ans for each execution. At the end, increase ans by a[1] and output it. Remember to check if an element you're going to decrease by 1 is positive beforehand.
Correctness: Let's prove correctness of algorithm by induction on n. Base case is n = 3 in which ans = max(a[1], a[2], a[3]) and algorithm correctly computes it. Now take n ≥ 5 and consider it's of the form 2k + 1. To change a[n] and a[n - 1] into 0, we need to take x = k as it's the only possible x which affects their values and perform operations exactly max(a[n], a[n - 1]) number of times. It's both necessary and sufficient in order to change both of them into 0. After that, we can ignore both a[n] and a[n - 1] from the list and induction hypothesis ensures that executing algorithm on remaining elements finishes the game in the least number of moves. 
Implementation: C++
D. Restoring Table
Consider a[i], a[j] and b[i][j] = a[i]&a[j]. Now consider binary representation of b[i][j]. For each 1-bit of b[i][j] at position k, (0-indexed) we conclude that k-th bit of a[i] and a[j] equals 1 so we set a[i] = a[i]|2k and a[j] = a[j]|2k. Now let's describe algorithm. We use i to iterate from 1 to n and for each i, we iterate over all b[i][j] such that i ≠ j and assign a[i] = a[i]|b[i][j]. At the end, we'll have sequence a constructed. Now we prove correctness of algorithm.
Correctness: Consider 2 indices i and j such that a[i]&a[j] ≠ b[i][j]. Consider that k-th bit of a[i]&a[j] differs from k-th bit of b[i][j]. If k-th bit of their AND equals 0, we face contradiction as k-th bit of b[i][j] has to be 1 and algorithm ensures that in this situation, k-th bit of both numbers will be set as 1. On the other hand, if k-th bit of their AND equals 1 then we conclude that k-th bit of both numbers equals 1 hence when calculating AND of them, we get 1 in k-th bit which is a contradiction with our preliminary hypothesis. So we proved correctness of algorithm. 
Implementation: C++
E. Mishap in Club
Consider following interpretation of problem. We're standing in (0, 0) at the center of Cartesian coordinate system. We iterate over the given sequence, for each + , we move from (x, y) to (x + 1, y + 1) and for each - , we move from (x, y) to (x + 1, y - 1). Consider the maximum y coordinate we visit during our movement as MAX and minimum y we visit as MIN. It's obvious that we need at least MAX - MIN people. It can be proved that we can take our moves in such a way that we exactly need MAX - MIN people. For each + , if there exists a person out of cafe who had entered cafe once or was in cafe once, we move him in, otherwise, we need a new person. The same argument holds for each - we see in sequence.
Implementation: C++
F. Log Stream Analysis
First note that "MESSAGE" is useless and can be ignored. Year is always 2012 so it can be ignored too. Now convert each date and time to seconds past from beginning of 2012. Maintain a list, such as a vector, V, for storing seconds. Define pointer head to be head of your vector. Define sec to be conversion of date and time in seconds for the most recent log. As long as head ≤ Size[V] and V[head] + n ≤ sec, increase head. After that, push sec into V. If Size[V] - head ≥ m then answer is the current log. If at the end, no time was found, answer will be - 1.
Implementation Note: You may use stringstream in order to ease implementation part. More information can be found here and here.
Implementation: C++
G. Suggested Friends
Use map in order to map people to numbers. Construct the given graph using adjacency list. Now, let's find answer for each vertex v. Mark all of v's neighbors. After that iterate over all other vertices, and iterate over their adjacency list and count their mutual neighbors with v and update answer for v. Complexity is O(m) for each vertex v. Summing up all complexities, we conclude that our algorithm is of O(nm) and as n is of O(m), we can conclude that overall complexity is O(m2).
Implementation: C++
H. Queries for Number of Palindromes
Note: Strings and arrays are considered 0-based in the following solution.
Let isPal[i][j] be 1 if s[i...j] is palindrome, otherwise, set it 0. Let's define dp[i][j] to be number of palindrome substrings of s[i...j]. Let's calculate isPal[i][j] and dp[i][j] in O(|S|2). First, initialize isPal[i][i] = 1 and dp[i][i] = 1. After that, loop over len which states length of substring and for each specific len, loop over start which states starting position of substring. isPal[start][start + len - 1] can be easily calculated by the following formula:
isPal[start][start+len-1] = isPal[start+1][start+len-2] & (s[start] == s[start+len-1])
After that, dp[start][start + len - 1] can be calculated by the following formula which is derived from Inc-Exc Principle.
dp[start][start+len-1] = dp[start][start+len-2] + dp[start+1][start+len-1] - dp[start+1][start+len-2] + isPal[start][start+len-1]
After preprocessing, we get queries li and ri and output dp[li - 1][ri - 1]. Overall complexity is O(|S|2).
Implementation: C++











Well-written,resourceful editorial...thanks to the writer!
Can we solve this question by some means if the constraints are :
Size of string = 10^5
No. of Queries = 10^5
Did you find the solution?
Can someone explain the hashing solution for problem H
The official solution to Problem H (c++) is giving a "Time limit exceeded on test 5".
Use '\n' instead of endl.
I got tle for using endl. After using "\n" it passes with time less than 2 second.
In problem H, submitting even the editorial implementation gives TLE on test case 5.[Not even using "\n" instead of endl].
for 245D - Восстановление таблицы
3 -1 1 4 1 -1 1 4 1 -1
this input will out a wrong answer, 5 1 5 note that a1 & a3 = 5 & 5 = 5 != b[1][3]
in h how to think of that dp transition