Given an array of N(N<=10^5) elements and -10^9<=A[i]<=10^9. Q(Q<=10^5) queries are there of two types:
- L R K: Add K to all numbers in range [L,R] in array.
- L R: Find no. of positive elements>0 in range [L,R].
I Thought of segment tree with lazy propagation but not able to understand what info to be stored in each node. Please suggest some approach for this problem.











is K non-negative or can K be negative?
K is positive.
So you can try using sqrt-decomposition.
Divide the array into blocks of size sqrt(n). For each block store the number of positive elements in it and a set containing all negative elements in it.
For query of type 2: just add the number of positive elements in all blocks between l to r.
For type 1: for all blocks between l to r, just erase all the elements from its set that are >-k and increment the number of positive elements in that block correspondingly.
Here what will be the complexity for erase operation?? I think erase operation may increase the time complexity.
it will be O(log(sqrt(n)) for each erase...and you erase each element at most once.
Since K is positive, once the number on some index becomes positive, it stays positive until the end.
Let's build a segment tree supporting range additions and range maximum queries. For queries of first type, simply update the range.
For queries of second type, while the maximum in the range is positive, take it, mark it in another segment/Fenwick tree as positive and make it equal to -INF in the original segment tree (simply update the index with - 1018) so that it never becomes positive again. Now the answer is simply the range sum in the second segment/Fenwick tree.
It's easy to see that the complexity is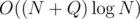 .
.
P_Nyagolov Thanks for the reply. I understood the method for query of first type like create a segment tree where in each node we store the maximum value in the range covered by that node and range addition using lazy propagation.
However not able to understand the second part as I am just storing the maximum of the range covered by a node, so how to process the positive values in that range one by one.?? Please explain.
Alright, let's say that our array is
[1, - 4, - 7, 2, - 1]
at some point and we have marked positive numbers so far in another array:
[1, 0, 0, 1, 0].
Now let's set all positive numbers to - ∞ so that after each update, the only positive numbers are the unmarked ones:
[ - ∞, - 4, - 7, - ∞, - 1].
Now we perform an update on the whole array with K = 5.
The new array should become
[ - ∞, 1, - 2, - ∞, 4].
After that update, consider a query for range [2;5], we use 1-based indexing.
So there we go, take the maximum in that [2;5] subarray. It is the one on position 5. We set it to - ∞ and mark it as positive in the other array:
[ - ∞, 1, - 2, - ∞, - ∞]
[1, 0, 0, 1, 1].
Take the maximum again, it is the one on index 2. Set it to - ∞ and mark it as positive:
[ - ∞, - ∞, - 2, - ∞, - ∞]
[1, 1, 0, 1, 1].
Take the maximum again, it is the one on index 3. However, it's not positive anymore, so there are no more positive integers in that range. So we stop there and report the range sum in the second array (1 + 0 + 1 + 1 = 3) as the answer to the query.
Setting a number to - ∞ can be done by simply updating its index with - 1018 as I mentioned before.
Hey Lakh!
Can you provide the link to the question ?