Hello everybody!
I'm delighted to invite you to anniversary round AtCoder Beginner Contest 100, which starts at Saturday, June 16, 2018 at 21:00 JST. The time is as usual as previous round. (However, some of AtCoder contest start time is unusual...)
This is the fifth round for a Japanese twin-brothers: E869120 and square1001. I already held AtCoder Beginner Contest 064, 076, 088, 096, and this time, it's 100. Multiple-of-four again, again and again! (Where is the probability 1/1024 ???) Anyway, ultimate thanks for rng_58 for reviewed and refined my problems, chokudai for creating one of the best contest platform in the universe. It is obvious that I could not be able to host the contest without cooperation of these two people.
The round is rated for participants whose rating is strictly lower than 1200. High-skilled participants whose rating is >=1200 is also welcomed to participate as out of competition (unrated).
Scoring is 100 — 200 — 300 — 400, as usual. The contest duration is 100 minutes.
Let's participate in the contest, good luck and high rating! Also, hope to have a ultimate-great memory in the first 3-digit round!
Finally, AtCoder managed to hold the contest which the first-digit is not '0'. Since this contest is the 100th anniversary round, so some problem can be associated with anniversary. Wish AtCoder and other contest platforms will be continue till 4-digit round :)
UPDATE
1. Judge queue is clogging now.
2. Now, judge queue is fixed. Sorry for inconvenience.
3. Editorial Uploaded.











I'm delighted to invite you to anniversary round AtCoder Beginner Contest 100, which starts at Monday, June 16, 2018 at 21:00 JST. The time is as usual as previous round.I think it's Saturday.
Oh no, it's a mistake. Fixed. :)
Nice announcement :)...Hope Problems too
You guys are my favourite problem setters, and I try to never miss any of your contests !
Last time, you guys had that problem "Five, five everywhere" and before that "Takashaki Information" which I liked a lot.
I hope there are good problems tomorrow as well !
P.S. — How come you guys don't hold parallel Regular Contest ?
Thank you, ghoshsai5000 to reply for my blog.
P.S. — How come you guys don't hold parallel Regular Contest ?
This is our 5-th AtCoder Beginner Contest. To hold ABC 064, 076, 088, 096 and 100, I learned a lot about the fundamental and practical use of hosting a good contest: e.g.) how to make good problems, how to prepare a contest faster, and how to make you understood the problem statement for Japanese. (Thank you very much, AtCoder.)
After a year of learning, finally, I am already thinking to do an adventure: to host a Regular Contest.
Anyway, good luck and have fun in this beginner contest. I'm looking forward to your participation and your rating increase!
I also want to know how to make good problems, how to prepare a contest faster and how to make me understand the problem statement for Japanese >///<
I see you have become red on AtCoder ... Congratulations !
[Reminder] The round will start in 3 hours and 30 minutes. Have fun!
Seems like there are some problems on judge queue. I sended messages 10 minutes before of this contest to two admins (rng_58, chokudai) but no reply now. Sorry for inconvenience but the writers can't do anything.
UPD: Got a response to admins. Since there are many participants, there are many source codes to judge. Therefore, there was (or is?) a judge queue.
UPD2: There were 50 judge servers today, and from 22 minutes after contest start they boosted to 170 judge servers. From the next time, the number of judge servers will be 100.
[General Announcement]
Judge queue is now fixed.
Well that was easier than expected.
Early lunch for me! :D
( I'm not speaking too soon, am I? Are there systems tests or hacks? )
There are no system tests or challenge in AtCoder.
Anyway, thank you for your participation!
How to solve D?
There can be 8 possibilities- beauty(+,-)(net sum of beauty is positive or negative in chosen values, similarly for others), taste(+,-), popularity(+,-) -> 2*2*2=8.
So, you can check in all these 8 cases. Thus you are left with finding m maximum values from an array(sum for each dish of (1/-1)beauty + (1/-1)taste + (1/-1)*popularity) which is quite easy.
Here’s how I solved it:
For each cake i from 1 to n
For all other cakes j from 1 to n where i != j, find the sum of the m-1 greatest values (S) computed like this:
then the candidate max is (abs(x[i]) + abs(y[i]) + abs(z[i])) + S.
We wish to either maximise or minimise each of ,
, 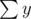 and
and 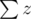 , as these correspond to the greatest absolute values (i.e they should be really positive or really negative). Iterate over the 8 possibilities of max- and min-imisation of
, as these correspond to the greatest absolute values (i.e they should be really positive or really negative). Iterate over the 8 possibilities of max- and min-imisation of  ,
, 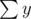 and
and 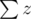 (i.e trying to make all three of them large positive, then making
(i.e trying to make all three of them large positive, then making  and
and 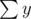 large positive and
large positive and 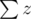 large negative, ... and so forth).
large negative, ... and so forth).
Then each value ai contributes a fixed value to the sum of the absolute values, and we append all of these to an array, sort it in reverse, then find the sum of the first m elements.
The answer is the maximum of the eight sums obtained.
I hope that makes sense, though I would imagine it does not, so please feel free to ask for clarifications and view my submission here
solution for D?? I have seen these type of questions but fail to do it every time
EDIT: Also, B was good. almost pulled my hair solving that.
But, B was superb!
Please explain the bonus solution to C.
My feedback to this contest is that problem C could have been worded much clearer.
In the "bonus" solution that you can solve C with O(Nloglogai), you should do following things:
First, let f(x) be "how many times can you divide x by 2". For example, f(6) = 1, f(144) = 4, f(1024) = 10.
The answer is obvious, you should print f(a1) + f(a2) + f(a3) + ... + f(aN).
So, you should determine the value of f(x) with O(loglogx) complexity.
To solve this, you can use binary-search by the value of f(x).
If x is divided by 2M, f(x) is more than or equal to M, and otherwise, f(x) is less than M.
Let's explain about the example of f(160).
The maximum value of f(x) is O(logx), so the complexity to get the value of f(x) is O(loglogx).
I see ! Rather than divide by 2 continuously, binary search and check if 2^M divides X.
If 2^M divides X, then answer >= M
If 2^M doesn't divide X, then answer < M
So, binary search for M in [1, 32],
Take the middle value every time. If 2^M divides X, then cut out the left half. Else, cut out the right half. Very nice !
So, I learnt that you can find the highest exponent of a prime P in a number N using binary search today !
We've (writers + camypaper) found more efficient, worst time complexity O(N + log amax) solution, if the bitwise operation of ai-order numbers can be calculated in O(1).
First, the bitwise AND of x, - x is exactly gcd(x, 2∞). It is commonly used in implementing Fenwick Tree. You can see why from this stackoverflow.com question.
Second, let ei = ai AND ( - ai). Now ai is in 2b form. Think about counting number of 20, 21, 22, ..., 2log amax in e1, e2, e3, ..., eN. We can take modulos. For example, 20, 21, 22, ..., 235 modulo 37 is all different. This means 37 has primitive root 2. Therefore, if you calculate ei modulo 37, only size 37 array is used to count the number of ei = 20, 21, 22, ....
The time complexity is O(N + log amax) if amax is about 230.
Actually, the time complexity don't change for any amax (but still conjecture). You can check Artin's conjecture of primitive roots and prime number theorem. If Artin's conjecture is true, letting k = log amax, the minimal modulo will be k + O(log k). Therefore, if you already find such minimal modulo, you can calculate in O(N + k) = O(N + log amax).
Thanks for this amazing Solution.I am a big fan of yours (:
Now, editorial is out.
Sorry for the server issue (which delayed your judge up to 12 minutes). Anyway, thank you for your participation!
square1001, E869120
Nice editorial with clear explanations!