Разбор чемпионата Баранович 20.06.2018

#	User	Rating
1	tourist	4009
2	jiangly	3823
3	Benq	3738
4	Radewoosh	3633
5	jqdai0815	3620
6	orzdevinwang	3529
7	ecnerwala	3446
8	Um_nik	3396
9	ksun48	3390
10	gamegame	3386

#	User	Contrib.
1	cry	167
2	Um_nik	163
3	maomao90	162
3	atcoder_official	162
5	adamant	159
6	-is-this-fft-	158
7	awoo	157
8	TheScrasse	154
9	Dominater069	153
9	nor	153

Все задачи находятся в последнем соревновании группы

А - Добро пожаловать в бан

Автор: Xijiks

В этой задаче требовалось вывести "BAN".

Решение (С++)

#include <bits/stdc++.h>

using namespace std;

int main() {
    ios_base::sync_with_stdio(false);
    cout << "BAN";
    return 0;
}

B - ♫ Цвет настроения синий ♫

Автор: Xijiks

Нужно было найти количество чисел от 1 до N, которые при делении на 5 дают остаток 4. Это можно было сделать обычным циклом. Асимптотика такого решения O(N).

Также эту задачу можно было решать за O(1). Нужно было заметить, что ответ всегда равен 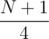$\text{[math]}$ .

Решение (С++)

#include <bits/stdc++.h>

using namespace std;

int main() {
    ios_base::sync_with_stdio(false);
    int n;
    cin >> n;
    int cnt = 0;
    for (int i = 1; i <= n; ++i) {
        if (i % 5 == 4) {
            ++cnt;
        }
    }
    cout << cnt;
    return 0;
}

Решение с формулой (С++)

#include <bits/stdc++.h>

using namespace std;

int main() {
    ios_base::sync_with_stdio(false);
    int n;
    cin >> n;
    cout << (n + 1) / 5;
    return 0;
}

C - Защита 10 из 10

Автор: Artemx

Даны 3 числа. Нужно было проверить, правда ли, что сумма каких-то двух из них равна третьему. Проверяем.

Решение (С++)

#include <bits/stdc++.h>

using namespace std;

int main() {
    ios_base::sync_with_stdio(false);
    int a, b, c;
    cin >> a >> b >> c;
    cout << ((a + b == c || a + c == b || b + c == a)? "YES" : "NO");
    return 0;
}

Нужно было найти сумму кубов от 1 до N. Можно пройтись циклом и проссумировать. У многих была ошибка, связанная с переполнением типов данных. Многие писали что-то, похожее на это:

var
  i, n : longint;
  sum : int64;
begin
  readln(n);
  for i := 1 to n do
    sum := sum + i * i * i;
  write(sum);
end.

и получали неправильный ответ. Несмотря на то, что sum — переменная типа int64 (или long long в C++), если i имеет тип int, то произойдет переполнение при умножении. Так как в паскале переменная цикла for не может иметь тип int64, можно использовать цикл while. Асимптотика данного решения O(N).

Также можно решить за O(1). Существуют формулы:

$\text{[math]}$

$\text{[math]}$

$\text{[math]}$

Решение (Pascal)

var
  i, n : longint;
  sum, x : int64;
begin
  readln(n);
  for i := 1 to n do
    begin
      x := i;
      sum := sum + x * x * x; 
    end;
  write(sum);
end.

Решение (С++)

#include <bits/stdc++.h>

using namespace std;

int main() {
    ios_base::sync_with_stdio(false);
    int n;
    cin >> n;
    long long ans = 0;
    for (long long i = 1; i <= n; ++i) {
        ans += i * i * i;
    }
    cout << ans;
    return 0;
}

Решение с формулой (С++)

#include <bits/stdc++.h>

using namespace std;

typedef long long ll;

ll sqr(ll x) {
    return x * x;
}

int main() {
    ios_base::sync_with_stdio(false);
    ll n;
    cin >> n;
    cout << sqr(n * (n + 1) / 2);
    return 0;
}

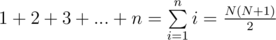
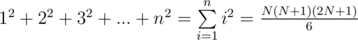
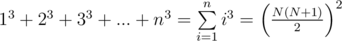
E - Шшшшшумы

Автор: Xijiks

Нам был дан массив, нужно в нём каждый 0 заменить на минимальное из рядом стоящих чисел, при этом гарантируется рядом с каждым 0 стоит два не нуля. Пройдемся по массиву и сделаем сделаем то, что просят. Асимптотика O(N).

Решение (С++)

#include <bits/stdc++.h>

using namespace std;

int a[100000 + 1];

int main() {
    ios_base::sync_with_stdio(false);
    int n;
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
    }
    for (int i = 1; i <= n; ++i) {
        cout << (a[i] ? a[i] : min(a[i - 1], a[i + 1])) << " ";
    }
    return 0;
}

F - Квадратные дата-центры

Автор: Xijiks

Дано число, найти ближайший к нему полный квадрат (модуль разности с которым минимален). С данными ограничениями можно было просто проверить все полные квадраты, которые не превосходят 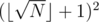$\text{[math]}$ , и вывести тот, модуль разности с которым минимален. Асимптотика такого решения $\text{[math]}$ .

Можно решать за O(1). Пусть X = trunc(sqrt(N)). Тогда ответом является X либо (X + 1). Из двух вариантов выберем оптимальный.

Ещё одно O(1) решение: можно заметить, что ответ всегда равен round(sqrt(N))².

Стоит отметить, если бы ограничения были больше, например, N ≤ 10¹⁸ функция sqrt сильно бы потеряла точность и ответ мог отличаться на 1, в этом случае для нахождения квадратного корня можно было бы использовать бинарный поиск. Можно также использовать sqrtl в C++. А можно было поступить иначе: пусть X = trunc(sqrt(N)). Проверим, что (X + 1)² ≤ N, если это так, то увеличим X на 1.

Решение (С++)

#include <bits/stdc++.h>

using namespace std;

int main() {
    ios_base::sync_with_stdio(false);
    int n;
    int d = (int)1e9, ans;
    cin >> n;
    int x = (int)trunc(sqrt(n));
    for (int i = 1; i * i <= (int)1e7; ++i) {
        if (abs(i * i - n) < d) {
    	    d = abs(i * i - n);
    	    ans = i * i;
	}
    }
    cout << ans;
    return 0;
}

Решение 2 (С++)

#include <bits/stdc++.h>

using namespace std;

int main() {
    ios_base::sync_with_stdio(false);
    int n;
    cin >> n;
    int x = (int)trunc(sqrt(n));
    cout << (n - x * x < (x + 1) * (x + 1) - n ? x * x : (x + 1) * (x + 1));
    return 0;
}

Решение 3 (С++)

#include <bits/stdc++.h>

using namespace std;

int main() {
    ios_base::sync_with_stdio(false);
    int n;
    cin >> n;
    int x = (int)round(sqrt(n));
    cout << x * x;
    return 0;
}

G - MusicSearch.com

Автор: fivut

Нас просят отсортировать массив и удалить повторяющиеся в нём числа. Отсортируем массив. Уникальными будут те числа в массиве, которые не равны предыдущему. Асимптотика O(N²) или O(N·logN) в зависимости от типа сортировки (пузырьком или быстрой).

Также можно было отсортировать массив и использовать встроенную в С++ функцию unique. O(N·logN).

Ещё можно использовать set в C++. Просто добавим весь наш массив в set и выведем это множество. O(N·logN).

Решение (C++)

#include <bits/stdc++.h>

using namespace std;

int a[1000 + 1];

int main() {
    ios_base::sync_with_stdio(false);
    int n;
    cin >> n;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
    }
    sort(a + 1, a + n + 1);
    a[0] = -1;
    vector<int> b;
    for (int i = 1; i <= n; ++i) {
        if (a[i] != a[i - 1]) {
            b.push_back(a[i]);
        }
    }
    cout << (int)b.size() << "\n";
    for (int x : b) {
        cout << x << " ";
    }
    return 0;
}

Решение с unique (C++)

#include <bits/stdc++.h>

using namespace std;

#define all(x) x.begin(), x.end()

int main() {
    ios_base::sync_with_stdio(false);
    int n;
    cin >> n;
    vector<int> a(n);
    for (int i = 0; i < n; ++i) {
        cin >> a[i];
    }
    sort(all(a));
    a.erase(unique(all(a)), a.end());
    cout << (int)a.size() << "\n";
    for (int x : a) {
        cout << x << " ";
    }
    return 0;
}

Решение с set (C++)

#include <bits/stdc++.h>

using namespace std;

int main() {
    ios_base::sync_with_stdio(false);
    int n;
    cin >> n;
    set<int> s;
    for (int i = 0; i < n; ++i) {
        int x;
        cin >> x;
        s.insert(x);
    }
    cout << (int)s.size() << "\n";
    for (int x : s) {
        cout << x << " ";
    }
    return 0;
}

H - [название]

Автор: Artemx

Нам дана матрица из X и O. Нужно найти количество X, вокруг которых ещё 4 символа X. Пройдемся циклом и проверим. У некоторых была ошибка, связанная с обращением к несуществующему индексу массива. Например при проверке клетки [N][M] проверялось наличие крестика в клетке [N + 1][M + 1], в разных средах эта ошибка могла отработать с разными последствиями. Следовало сделать циклы не от 1 до N и от 1 до M, а вместо этого циклы от 2 до N - 1 и от 2 до M - 1. Итого мы 1 раз прошли матрицу, каждую клетку проверили за O(1). Итоговая асимптотика O(N·M).

Решение (Pascal)

var
  a : array[1..500, 1..500] of char;
  i, j, ans, n, m : longint;
begin
  readln(n, m);
  for i := 1 to n do
    for j := 1 to m do
      begin
        if j = m 
          then readln(a[i, j])
          else read(a[i, j]);
      end;
  for i := 2 to n - 1 do
    for j := 2 to m - 1 do
      if (a[i, j] = 'X') and (a[i - 1, j - 1] = 'X') and(a[i - 1, j + 1] = 'X')
      and (a[i + 1, j - 1] = 'X') and (a[i + 1, j + 1] = 'X') then inc(ans);
  write(ans);
end.

Решение (C++)

#include <bits/stdc++.h>

using namespace std;

char a[500 + 1][500 + 1];

bool isCross(int x, int y) {
    int cnt = 0;
    if (a[x - 1][y - 1] == 'X') ++cnt;
    if (a[x - 1][y + 1] == 'X') ++cnt;
    if (a[x][y] == 'X') ++cnt;
    if (a[x + 1][y - 1] == 'X') ++cnt;
    if (a[x + 1][y + 1] == 'X') ++cnt;
    return cnt == 5;
}

int main() {
    ios_base::sync_with_stdio(false);
    int n, m;
    cin >> n >> m;
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            cin >> a[i][j];
        }
    }
    int ans = 0;
    for (int i = 2; i <= n - 1; ++i) {
        for (int j = 2; j <= m - 1; ++j) {
            if (isCross(i, j)) {
                ++ans;
            }
        }
    }
    cout << ans;
    return 0;
}

I - Выбор аватарки

Автор: fivut

Нам дали 4 точки в случайном порядке, нужно проверить, являются ли они прямоугольником, параллельным осям коррдинат и имеющим ненулевую площадь. Самое простое решение: введем 4 точки в vector < pair < int, int > > в С++. Отсортируем этот вектор, и теперь уже несложно проверить, удовлетворяют ли они условию. Подробности в коде. Асимптотика O(1).

Решение (С++)

#include <bits/stdc++.h>

using namespace std;

#define fi first
#define se second

typedef long long ll;

int main () {
    ios_base::sync_with_stdio(false);
    vector<pair<int, int> > a(4);
    for (int i = 0; i < 4; ++i) {
        cin >> a[i].fi >> a[i].se;
    }
    sort(a.begin(), a.end());
    if (a[0].fi == a[1].fi && a[1].se == a[3].se && a[3].fi == a[2].fi && a[2].se == a[0].se) {
        ll s = 1LL * (a[1].se - a[0].se) * (a[3].fi - a[1].fi);
        if (s) {
            cout << "YES\n" << s;
	} else {
            cout << "NO\n";
        }
    } else {
        cout << "NO\n";
    }
    return 0;
}

J - Страшная тайна ключей

Автор: Artemx

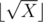В задаче нам дали массив, нужно найти сумму простых чисел в нём или вывести -1, если в массиве нет простых чисел. Для решения нужно уметь проверять число на простоту за $\text{[math]}$ . Проверить число X на простоту можно следующим способом: если X делится без остатка хоть на одно число от 2 до $\text{[math]}$ , то оно составное, иначе простое. N чисел проверяем на простоту за 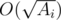$\text{[math]}$ . Итоговая асимптотика $\text{[math]}$ .

Решение (С++)

#include <bits/stdc++.h>

using namespace std;

bool isPrime(int x) {
    if (x == 1) return false;
    for (int i = 2; i * i <= x; ++i) {
        if (x % i == 0) return false;
    }
    return true;
}

int main() {
    ios_base::sync_with_stdio(false);
    int n;
    cin >> n;
    long long ans = 0;
    while (n--) {
        int x;
        cin >> x;
        if (isPrime(x)) {
            ans += x;
        }
    }
    cout << (ans == 0 ? -1 : ans);
    return 0;
}

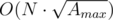K - IP-адреса

Автор: Xijiks

Дана строка длиной не более 15, состоящая из цифр и точек. Необходимо было проверить, является ли она правильным IP. Правильный IP — X.X.X.X, где 0 ≤ X ≤ 255. Заметим, что если в строке не 3 точки, то ответ "NO". Иначе проверим, что никакие две точки не стоят рядом, а числа между точками не имеют лидирующих нулей и не превосходят 255. Задача на реализацию, детали смотрите в коде. Асимптотика O(length(S)).

Решение (С++)

#include <bits/stdc++.h>

using namespace std;

#define sz(a) (int)a.size()

typedef long long ll;

string s;

ll getNum(int l, int r) {
    ll x = 0;
    if (l > r || (s[l] == '0' && l != r)) {
        cout << "NO";
        exit(0);
    }
    for (int i = l; i <= r; ++i) {
        x = x * 10 + (s[i] - '0');
    }
    return x;
}

int main() {
    ios_base::sync_with_stdio(false);
    cin >> s;
    vector<int> ind;
    for (int i = 0; i < sz(s); ++i) {
        if (s[i] == '.') {
            ind.push_back(i);
        }
    }
    if (ind.size() != 3) {
        cout << "NO";
        return 0;
    }
    ll a, b, c, d;
    a = getNum(0, ind[0] - 1);
    b = getNum(ind[0] + 1, ind[1] - 1);
    c = getNum(ind[1] + 1, ind[2] - 1);
    d = getNum(ind[2] + 1, sz(s) - 1);
    cout << (max({a, b, c, d}) < 256 ? "YES" : "NO");
    return 0;
}

L - GG WP, N00bs!

Автор: Artemx

Нужно было найти подмножества массива максимального размера, в котором разность между максимальным и минимальным элементом не превосходит X. Отсортируем массив и заметим, что искомым подмножеством является непрерывный отрезок массива. Переберём его правую границу R, тогда бинарным поиском найдем первое число в массиве, которое ≥ a_R - X, пусть его индекс равен L. Обновим ответ длиной отрезка, равной R - L + 1. Сортируем за O(N·logN) и N раз используем бинарный поиск, работающий за O(N·logN). Итоговая асимптотика O(N·logN + N·logN) = O(N·logN).

Задачу можно было решать скользящим окном (методом двух указателей). Отсортируем массив. Будет поддерживать две переменные L и R, для каждого значения R найдем минимальное значение L при котором a_R - a_L ≤ X. Для каждого R найдем соответствующее L и обновим ответ величиной R - L + 1. Левая и правая граница суммарно передвинутся не более 2·N раз. Значит наше окно работает за O(N). O(N·logN) на сортировку. Получаем асимптотику O(N + N·logN) = O(N·logN).

Решение (С++)

#include <bits/stdc++.h>

using namespace std;

int a[100000 + 1];

int main () {
    ios_base::sync_with_stdio(false);
    int n, x;
    cin >> n >> x;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
    }
    sort(a + 1, a + n + 1);
    int ans = 1;
    for (int r = 1; r <= n; ++r) {
        int l = lower_bound(a + 1, a + n + 1, a[r] - x) - a;
        ans = max(ans, r - l + 1);
    }
    cout << ans;
    return 0;
}

Решение с окном (С++)

#include <bits/stdc++.h>

using namespace std;

int a[100000 + 1];

int main () {
    ios_base::sync_with_stdio(false);
    int n, x;
    cin >> n >> x;
    for (int i = 1; i <= n; ++i) {
        cin >> a[i];
    }
    sort(a + 1, a + n + 1);
    int ans = 1;
    for (int l = 1, r = 1; r <= n; ++r) {
        while (a[r] - a[l] > x) {
            ++l;
        }
        ans = max(ans, r - l + 1);
    }
    cout << ans;
    return 0;
}

M - Админ по имени Лёха

Автор: fivut

Нам был дан двумерный массив из 0 и 1. Требовалось найти квадрат с максимальной площадью, в котором ≤ S единиц. Для решения этой задачи требовалось за O(1) находить сумму в любом прямоугольнике матрицы. Сделать это можно с помощью префиксных сумм на матрице. Переберем верхний левый угол нашего квадрата и длину стороны квадрата. Таким образом мы переберём все квадраты в матрице. Мы можем обновить ответ текущей длиной квадрата, если в этом квадрате ≤ S единиц. Сумму в квадрате найдем с помощью префиксных сумм. Получается мы перебираем угол квадрата за O(N·M), его сторону за O(min(N, M)) и за O(1) находим в нём сумму. Асимптотика O(N·M·min(N, M)).

Бонус1: Попробуйте решить задачу за время O(N·M).
Бонус2: Попробуйте найти прямоугольник с максимальной площадь в матрице.

Решение (С++)

#include <bits/stdc++.h>

using namespace std;

const int N = 333;

int pref[N][N];

int countTrees(int x, int y, int x2, int y2) {
    return pref[x2][y2] - pref[x - 1][y2] - pref[x2][y - 1] + pref[x - 1][y - 1];
}

int main() {
    ios_base::sync_with_stdio(false);
    int n, m, s;
    cin >> n >> m >> s;
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            char c;
            cin >> c;
            pref[i][j] = pref[i][j - 1] + pref[i - 1][j] - pref[i - 1][j - 1] + (c == '#');
        }
    }
    int ans = 0;
    for (int i = 1; i <= n; ++i) {
        for (int j = 1; j <= m; ++j) {
            for (int k = 1; k <= min(n, m); ++k) {
                int x2 = i + k - 1;
                int y2 = j + k - 1;
                if (x2 > n || y2 > m) break;
                if (countTrees(i, j, x2, y2) <= s) {
                    ans = max(ans, k);
                }
            }
        }
    }
    cout << ans;
    return 0;
}