bukunu's blog

Given three arrays, find elements a,b,c such that a+b=c.

By bukunu, history, 6 years ago, In English

Asked in a Finance Company Interview :

Given three unsorted arrays A,B and C, the task is to find three elements a,b,c from the three arrays such that a+b=c.

Can it be done in O(nlogn)?

Suppose the arrays are given as sorted, then can it be done in linear time?

  • Vote: I like it
  • +11
  • Vote: I do not like it

»
6 years ago, # |
  Vote: I like it +26 Vote: I do not like it

Currently the best I have is that if the maximal value of an element in one of the arrays is M, then we can find all possible sums of arrays A, B in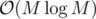 using fft, and then sort array C in 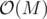and find a common value in .

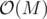I might be missing something clear.

→ Reply
»
6 years ago, # |
  Vote: I like it +23 Vote: I do not like it

It appears that this problem is reducible to 3SUM. Therefore, it is unsolvable in less than O(n²) time if the values of the elements are unbounded.

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it +12 Vote: I do not like it

The problem looks similar enough to 3SUM problem, and for its general case, there's no known solution in : a deterministic solution better than O(n2) was invented only recently, in 2014.

Note that the Wikipedia page mentions the FFT solution presented above by Noam527 when the array elements are bounded integers.

→ Reply