Given an array of n integers (1<=n<=300000, 0<=arr[i]<=100000) and q queries (1<=q<=300000) where each query contains 2 integers l and r (1<=l<=r<=n), tell the gcd of all the elements in range l to r (both inclusive).
I am just not getting an idea on how to link query(l) and query(r) in fenwick tree(BIT)











Auto comment: topic has been updated by Riyuzak251097 (previous revision, new revision, compare).
I think (but I'm not sure) it can't be represented in BIT (Fenwick). But it can as segment tree.
ya i did implement it using a segment tree, just curious to find if we can do the same with a fenwick tree by using some gcd relation i maybe can't think of
I don't think so. Fenwick can't for example give you max and min queries. I don't think it's possible for gcd too.
Fenwick can easily answer queries whose have inverses, for example multiplication -> division, addition -> subtraction, xor -> xor.
Interesting , this fact really made me clear about when to use a fenwick tree
mmm you can build a fenwick tree where in each node x save information of array (x — (x&-x), x] i.e. gcd to left and right, then in each query you only consider segment intersection. (memory complexity O(nlog{n}), query complexity O(log^2{n})) :v ugly solution compared with segment tree, but cool idea.
Nice! In fenwick array we can store vectors of suffix gcd of [x-(x-x&-x,x] and we need to answer the queries just to the left as much as you can. Why is the complexity log^2(n)? It is log(n)*gcd. And i believe what with a[i]<=10^5 when we calculate gcd logn times numbers gets smaller and gcd counting terminates faster.
I think what calculating gcd many times is as hard as calculating gcd(a,b)=1
Hey i didn't get your approach, are you telling that we store the gcd from x — x & (-x) to x at that node and same for right? Can you just elaborate a little about your approach and how would we query?
As we know fenwick tree stores array A with index i storing information for (i-i&-i, i], so if we store auffix gcd, we can jump from (l, r) to (l, r-r&-r), or if l>=r-r&-r we can just get the answer.
Complexity actually is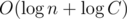 , where С is constraint on numbers in array. The second
, where С is constraint on numbers in array. The second 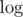 comes from Euclid's algorithm: you can consider amount of its steps during one query processing and show that it doesn't exceed
comes from Euclid's algorithm: you can consider amount of its steps during one query processing and show that it doesn't exceed 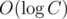 .
.
Just sort the query in decreasing L, and it can be done by BIT.
Oh! Offline solution is best in memory!
Could you explain your solution in more detail please?
Offline solution is good to change inverse with identity (0 in this case) then in you fenwick update gcd while traverse in order of sort.
Gonna ask this question in the Fenwick Tree section of the course???? Just Kidding.