Блог пользователя Learner99

Find number of MST in given Graph.
Автор Learner99, история, 6 лет назад, По-английски

Given an undirected weighted graph. How to find the total number of minimum spanning tree for that given graph.

Number of nodes <= 10. No parallel edges.

I found a similar problem here: https://www.spoj.com/problems/MSTS/

I don't want answer mod 31011 as asked in above Spoj Problem. I want the exact number of ways. (Though I don't know the solution of the Spoj problem either.)

Can someone please help me in solving this question?

Thanks in advance.

Happy Coding :)

  • Проголосовать: нравится
  • +8
  • Проголосовать: не нравится

»
6 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

Root tree at 1 and for each node x assign parent from 1 to x-1 this gives 9! possible trees.

→ Ответить
»
6 лет назад, # |
← Rev. 2   Проголосовать: нравится +28 Проголосовать: не нравится

  1. You can calculate the number of "spanning trees" with Kirchhoff's theorem. I guess this was O(N3). I don't know this well, but you can always google and copy paste.

  2. You can reduce this problem to counting the number of spanning trees. This works because you can think edges with different costs individually. To elaborate, suppose you are doing something for all edges with cost X. No matter what MST you chose, the components formed with edge cost < X is consistent (Think Kruskal's Algorithm!) Then you can think such components as a single node. You should now use some cost X edges, to merge the nodes as much as possible. This is exactly the number of spanning trees.

→ Ответить
»
6 лет назад, # |
  Проголосовать: нравится +3 Проголосовать: не нравится

I think that it is some dp[mask][x][y] is pair of minimum weight of tree with nodes having mask, and node x having degree y, and number of suck trees.

→ Ответить
»
6 лет назад, # |
  Проголосовать: нравится +9 Проголосовать: не нравится

The simplest algorithm that should work in your case is to simply handle all nn - 2 (up to 1010 - 2 = 108) possible spanning trees recursively, some care should be taken to make each step of the search take O(1) time. I would not dwell on the details, because one may do much better.

There is an algorithm for this problem, that is based on the matrix tree theorem and, curiously, does not require any complicated ideas beyond that. Title is misleading, this paper actually explains how to count MSTs too.

I can make a writeup of main ideas here, but it will be rather long, so I will do this only on request. Feel free to ask, though.

→ Ответить
  • »
    »
    6 лет назад, # ^ |
      Проголосовать: нравится 0 Проголосовать: не нравится

    It will be very helpful if you can elaborate on the main idea. Because I tried to read the paper but was not able to understand that.

    And about the brute force recursive solution actually, I have to find the answer of multiple queries. So this will definitely give TLE.

    → Ответить
    • »
      »
      »
      6 лет назад, # ^ |
        Проголосовать: нравится +6 Проголосовать: не нравится

      My notation does not completely match the notation in linked paper. Warning: I doubt that my explanation will be much clearer than the author's.

      1. Use weighted matrix tree theorem, where edge with weight w has weight xw.

      2. Suppose that the weight of MST is wmin and consider some MST T. Suppose that the vertex you throw out in matrix tree theorem (you can throw out any) is the root of T (moreover, we can think that this vertex is n). Denote the remaining (n - 1) × (n - 1) matrix as D(x).

      3. One may see that the number we are looking for is the coefficient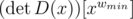 . Moreover, 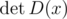is divisible by xwmin (wmin is the weight of MST, after all).

      4. On the other hand,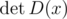 is obviously divisible by product of xck for k = 1, 2, ..., n - 1, where xck is the highest power of x that divides every element of the k-th column of D(x).

      5. One may hope that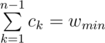 and after dividing k-th column of D(x) by xck we will get a matrix D0(x), whose entries are polynomials and the coefficient 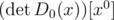is non-zero. In this case we could find 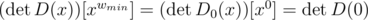. However, it would be naive to hope that: it is equivalent to Boruvka's algorithm for finding MST finishing in just one step.

      6. However, we may change D(x) slightly in such a way, that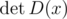 does not change, but sum of ck's becomes equal to wmin (a dream that we want to achieve)! To be exact, we will apply some standard column operations: add one column to the another.

      7. Now, the tree T will come in handy. Recall that the root of this tree was the thrown out vertex. How do we construct the modified matrix Dm(x)? k-th column of Dm(x) will be equal to the sum of i-th columns of D(x) for i ranging over vertices of the subtree of vertex k in T.

      8. Such a transformation can be carried out by means of row operations: just add each i-th column to the p-th column, where p is the parent of i in T, in order of decreasing depth (obviously, you can't do this operation, if p = n is the root of T, because Dm has only n - 1 columns; just don't do anything in this case).

      9. Now, one can notice that all entries in k-th column of Dm(x) are sums of xw with some coefficients, where w ranges over all weights of the edges that belong to the cut between subtree of k in T and the other vertices (by direct calculation, all the edges inside the subtree will cancel out: recall that k-th column of Dm(x) is the sum of i-th columns of D(x) with i ranging over subtree of k and notice that "positive" summands that correspond to the diagonal elements of D will cancel out with "negative" summands that correspond to the non-diagonal elements of D).

      10. Because T is minimal, the edge of this cut that belongs to T is exactly the edge of this cut with minimum weight. It follows that k-th column of Dm(x) is divisible by xck, where ck is the weight of edge in T that goes from the k to the parent of k. Therefore,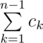 is equal to weight of T, which is equal to wmin. We achieved our dream! Now, return to the step 5 with matrix Dm(x) instead of D(x).

      → Ответить