A. Почти простые числа

Это задача на реализацию: для каждого числа от 1 до n разложим его на простые множители и посчитаем количество различных простых делителей.

B. Правильная скобочная подпоследовательность

Будем читать строку слева направо и поддерживать на каждом шаге баланс скобок (т.е. разность между количеством выписанных открывающих и закрывающих скобок). Этот баланс должен быть всегда неотрицательным. Поэтому если он равен нулю и мы читаем закрывающую скобку, ее нужно пропустить и не выписывать. Ответ будет равен удвоенному количеству выписанных закрывающих скобок.

C. Паркет

Докажем несколько необходимых условий для существования паркета. Если какое-то из них не выполнено, ответ "IMPOSSIBLE".
1. m*n должно быть четным, т.к. это общая площадь паркета, а площадь каждой плитки четна.
2. Допустим, что m (количество столбцов) нечетно. Раскрасим гостиную в черный и белый цвета следующим образом: первый столбец черный, второй белый, третий черный, ..., последний черный. Число черных квадратов будет на n больше, чем число белых. Плитки 1x2 и 2x2 содержат равное число черных и белых квадратов, поэтому разность нужно компенсировать с помощью плиток 2x1, и их число должно быть хотя бы n/2. В этом случае мы можем замостить последнюю колонку этими плитками, уменьшить b на n/2 и уменьшить m на единицу.
3. Если n нечетно, то аналогично получаем a ≥ m / 2.
4. Теперь  m и n четны. Похожие рассуждения показывают, что число использованных плиток 1x2 и 2x1 должно быть четным. Поэтому если a нечетно, уменьшим его на 1, и то же самое с b.
5. Теперь должно быть mn ≤ 2a + 2b + 4c, иначе не хватит общей площади плиток.
6. Если все условия были выполнены, мы можем завершить замощение: разделим гостиную на квадраты 2x2 и заполним каждый либо одной плиткой 2x2, либо двумя плитками 1x2, либо двумя плитками 2x1.

D. Билеты

Если мы изобразим график числа доступных 10-евровых банкнот, это будет ломаная линия с началом в точке (0, k) и концом в точке (m+n, n+k-m). Ровно m звеньев идут вниз, остальные n звеньев — вверх. Поэтому общее число возможных графиков равно C(m + n, m) (биномиальный коэффициент). Нам нужно найти число графиков, которые не заходят под ось X. Мы посчитаем "дополнительное" значение: число графиков, которые заходят под ось X, то есть пересекают прямую y=-1.

Для этого мы используем "принцип отражений". Рассмотрим любой график, который пересекает прямую y=-1, и возьмем последнюю из точек пересечения. Отразим часть графика, начиная с этой точки, относительно прямой y=-1. Получится новый график, оканчивающийся в точке (m + n,  - 2 - n - k + m). Обратно, любой график, оканчивающийся в этой точке, пересекает прямую  y=-1, и мы можем применить к нему ту же операцию. Итак, число графиков, которые нас интересуют, равно числу графиков, начинающихся в точке (0, k) и заканчивающихся в точке (m + n,  - 2 - n - k + m). Пусть a и b — число звеньев в таком графе, идущих вверх и вниз соответственно. Тогда a + b = m + n, a - b + k =  - 2 - n - k + m. Отсюда a = m - k - 1, и число таких графиков равно C(m + n, m - k - 1).

Таким образом, вероятность того, что график зайдет под ось X, равна C(m + n, m - k - 1) / C(m + n, m) = (m!n!) / ((n + k + 1)!(m - k - 1)!) = (m(m - 1)... (m - k)) / ((n + 1)(n + 2)... (n + k + 1)). Ответ к задаче: 1 — (m(m - 1)... (m - k)) / ((n + 1)(n + 2)... (n + k + 1)).

E. Multithreading

Ясно, что w должно удовлетворять неравенствам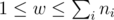 . Если это так, покажем, как достигнуть такого результата в трех случаях:
1. N = 1, w = n₁. Очевидно.
2. N ≥ 2, w ≥ 2. Для w = 2 схема такая: 1, все циклы процессов 3..N, n₂ - 1 циклов второго процесса, 1, 2, n₁ - 1 циклов первого процесса, 2. Для w > 2 нужно переместить несколько циклов из середины последовательности в конец.
3. N ≥ 2, w = 1, и существует i такое, что n_i = 1. Схема такая: i, все циклы остальных процессов, i.

Теперь покажем, что в остальных случаях результат w недостижим. Случай N = 1, w ≠ n₁ очевиден. Осталось разобрать ситуацию, когда N ≥ 2, w = 1, и n_i > 1 для всех i. Допустим, что существует последовательность, для которой результат оказался равным y = 1. Рассмотрим последнюю операцию записи в этой последовательности, пусть ее провел процесс с номером i. Тогда соответствующая операция чтения должна была прочитать значение y=0. Это значит, что до нее не было произведено ни одной операции записи. Но это невозможно, т.к. n_i > 1, и i-й процесс к этому моменту произвел n_i - 1 циклов чтения/записи.