Thanks to the many authors of this contest (all eight of them) for a great set of problems! I'll sketch out the solution ideas for a few of them here:
1019A - Elections
Let's assume our goal is to end the election with v votes and determine the minimum cost to do so.
First, we need to make sure every other party ends up with fewer than v votes. To do this, we should bribe enough people in every party to get them down to v - 1 votes or fewer. We can do this greedily by bribing the cheapest people in the party.
After that if we have v votes (or more), we are done. Otherwise, we should repeatedly bribe the cheapest voters remaining until we get to v. Note that we can do this in O(n) time rather than  by using an O(n) selection algorithm such as nth_element, though this wasn't necessary to pass the problem.
by using an O(n) selection algorithm such as nth_element, though this wasn't necessary to pass the problem.
Finally, simply loop over all possible values of v and take the minimum cost across all of them for an O(n2) solution.
Code: 41475525
In fact it is even possible to solve the problem in  . Here is a solution using ternary search on v: 41534204
. Here is a solution using ternary search on v: 41534204
1019B - The hat
Let 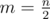 . Let's define the function d(i) = ai - ai + m. We are looking for i such that d(i) = 0. Notice that since |ai - ai + 1| = 1, d(i) - d(i + 1) must be - 2, 0, or 2.
. Let's define the function d(i) = ai - ai + m. We are looking for i such that d(i) = 0. Notice that since |ai - ai + 1| = 1, d(i) - d(i + 1) must be - 2, 0, or 2.
First query for the value of d(1). If it is odd, then every d(i) is odd due to our property above, so the answer is - 1. Otherwise every value d(i) is even. Notice that d(m + 1) = am + 1 - a1 = - d(1). This means that one of d(1) and d(m + 1) is a positive even value, and the other is a negative even value. Since consecutive values can only differ by - 2, 0, or 2, there must be an index i in between 1 and m + 1 that satisfies d(i) = 0, and we can use binary search to find this index.
Code: 41502076
: 1019D - Large Triangle
The obvious solution for this problem is O(n3), which can actually be squeezed in the time limit if you're careful; e.g., 41488961 and 41491248. However the real solution is  , which I'll describe here:
, which I'll describe here:
Since the area of a triangle is 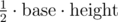 , if we picked two of the n points as our base, we would know exactly what height we needed in order to make a triangle with the goal area. In particular, if we had our points sorted by distance to this segment, we could use binary search to determine whether or not there was such a point in
, if we picked two of the n points as our base, we would know exactly what height we needed in order to make a triangle with the goal area. In particular, if we had our points sorted by distance to this segment, we could use binary search to determine whether or not there was such a point in  time.
time.
We can perform a rotational sweep on the set of points, which lets us set up this height-sorted list for every segment in order to solve the problem. (Imagine smoothly rotating the points clockwise, stopping whenever any two points are perfectly lined up horizontally.)
To do this we can take all n2 segments and sort them by angle. We also initialize our sorted list of points by y, breaking ties by x. We then iterate through our sorted segment list, swapping two points each time in order to maintain the height-sorted list. Finally we do two binary searches per segment to find if there are any points at the appropriate height (one above and one below).
Note that we can perform all these computations in integers only by using cross products. See the code below for details. Also, kudos to the problem writers for adding the guarantee that "no three cities lie on the same line," which helps keep the code cleaner without changing the key idea of the problem.
Code: 41502172
Unfortunately I don't know the solutions for C or E. If you do, leave a comment!











Can you elaborate on the binary search part in Div1 B? What's your binary search function?
Sure. Let's assume d(x) > 0 and d(y) < 0. Now take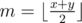 . If d(m) = 0 we're done. Otherwise if d(m) > 0, we know there is a valid answer between m and y, and if d(m) < 0, we know there is a valid answer between x and m.
. If d(m) = 0 we're done. Otherwise if d(m) > 0, we know there is a valid answer between m and y, and if d(m) < 0, we know there is a valid answer between x and m.
Note that the half of the range we are throwing out could also have a solution, but it doesn't matter since the half we are choosing is guaranteed to have a solution.
Thanks!. I have been stuck on this for like 30 mins. Turns out to be a stupid doubt.
If we are investigating range [L;R] than we take m = (L + R) / 2 and if d(1) * d(m) > 0 then r: = m, else l: = m
Kaban-5 provides a nice solution to 1019C - Sergey's problem in his comment here.
You can see my code here for an implementation of this algorithm: 41503956
E is easy, just centroids and interval tree of convex hulls, nothing special :D
This kind of task should appear more often :P
How dare you saying easy :(
Benq couldn't solve it so please chill out!!!
Now this is lame and pathetic. Please stop. You are not 'encouraging' Benq, you just annoy all of us.
Number of BBST operations used is n log n, right?
So examining your code I figured out that you create query for each i = 0..m - 1 in some vertex that has biggest value if you take path from root to this vertex. I don't understand why we should check only this vertex. Can you explain it please.
Oh, so I got this. This is because one of the ends of diameter of the tree is the farthest vertex from any. This is so smart. But time complexity is O(M * log(N)3) as for each query you make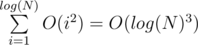 operations. So it seems like it should be TL.
operations. So it seems like it should be TL.
Yea, I also was afraid so I was writing this in a way so I'd be able to squeeze it and add breaks, but it turned out to be fast enough. It is O(m·log3(n)), but consider the fact that there isn't exactly log of n every time, the sizes of hulls are kind of summing up to n, so constant isn't so big.
Link on problem 1019A with larger constraints (n ≤ 105), do not lose it
Thanks neal, for providing great insights after every round! I also want to write my additional notes on this round.
Doing D without the "no three cities lie on the same line" condition : If there is a parallel segment, break ties by pair of (minimum point index, maximum point index). You can just add one more line for this. And this is enough! Code
My idea on E, which can be wrong as I didn't coded : Naively we can maintain an upper hull on every lines induced by a path. This is obviously too slow to fit in time, but hopefully we can reduce the path candidate by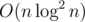 .
.
Do centroid decomposition on the given tree. For each centroid c find all lines that have its endpoint in c. We want to merge all pair candidates that comes from different subtree of c. We put all subtrees on heap and proceed like a Huffman coding (Work on two smallest subtree, and merge them as a single one)
For working on two smallest subtree we can generate their upper hull and do merge sort, which will generate all relevant candidate. Doing this for each centroid — now we have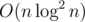 line segment candidate. We can now process all of these in
line segment candidate. We can now process all of these in 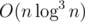 , which is kinda scary but I bet it'll run on time.
, which is kinda scary but I bet it'll run on time.
Nice, makes sense on D. We just need to make sure that every segment we get in order will swap two consecutive points in the height-sorted list. I still think it's better that the authors didn't require this, since I wouldn't want someone to figure out the key idea of the problem but fail due to messing up this part.
As for E, maybe Radewoosh can tell you whether his solution is or
or 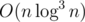 .
.
Now being serious: standard algorithm to find a diameter of the tree goes as follows: find vetted as far as possible from vertex 1, and then vertex as far as possible from this vertex. So firstly let’s calculate distances (by distance I mean sum of linear functions) from 1 to every other vertex, take convex hull of this function and for every i find one of vertices which will be an endpoint of a diameter in i-th day using binary search. Now for every vertex we know in which days it will be an endpoint.
Now let’s do centroid decomposition: with fixed centroid we can calculate distances from centroid to every vertex and then build interval tree over centroid’s subtrees, where in each vertex of interval tree we keep a convex hull of distances to vertices in subtrees which lie in this interval. Then, for each day (O(m)) for each centroid (O(log(n))) we want to check every other subtree (so O(log(n)) intervals) by doing a binary search (O(log(n))), so total complexity is O(m·log3(n)).
I think that m can be replaced with n by some tricks. For example I was using the fact that for each vertex the set of days when it’s the first endpoint is an interval and when doing k binary searches on some convex hull, where k is length of this interval, I was starting next binary search from the place when I’ve found last optimum. I think that with “if” “check if optimum stays in this same place” just by looking at neighbors, then it would magically amortize to O(n·log3(n)), but I’m not sure of that.
You can transfer the given tree into a tree where the degree of each node is at most 3. Then for each day, get one endpoint x, and for each centroid u, get the node with maximum distance to u for each of u's subtrees and update the answer. This can be done by keep a convex hull using a deque in O(1). So it would be O(n log2 n + m log n).
code here
Slower than yours.
My implementation does not construct the convex hull explicitly.
To me, E is one of those boring implementation problems where you know what to do, but there are enough things to do that you're going to make a bunch of silly mistakes. (I just solved it after fixing 3 bugs. 2 of them were TLE, easy to fix in-contest, and one was WA in very rare cases because I forgot that ax ≤ b, a > 0 doesn't convert to integer division x ≤ b / a for negative b with |b| < a, nearly impossible to catch by testing.)
Merging 2 already existing convex hulls can be done in O(number of segments in both), same with adding them. The resulting complexity is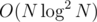 for construction of the final convex hull — one log comes from centroid decomposition, the other from making chulls and then the D&C. Finding the answer is just printing M values on the hull.
for construction of the final convex hull — one log comes from centroid decomposition, the other from making chulls and then the D&C. Finding the answer is just printing M values on the hull.
There are almost no clever ideas required for this — centroid decomposition, constructing convex hulls and the D&C approach are obvious, the only interesting part is doing sum of convex hulls instead of convex hull of pairwise sums. It's a garden variety "centroid decomposition with something" where that something is convex hull of pairs. (In fact, I think I solved something very similar this year.)
For the "Large Triangle" , how does swapping the points keep the points height-sorted ?
If we imagine taking all the points and rotating them slowly clockwise, the only times that the height-sorted list changes are when two points are lined up horizontally with each other. This is why we produce an angle-sorted list of segments, to simulate this rotation.
Do we always rotate all the points with respect to the center ?
It actually doesn't matter what point you're rotating around, since any segment will eventually rotate to being perfectly horizontal, regardless of the choice of point.
In terms of visualizing it though, I like to think of drawing every point on a giant sheet of paper and spinning the paper.
Thank you , finally got it.
Really helping, as the official editorial is a bit late. Thank you!
I believe your solution is actually
O(n^2log(n^2))for 1019D — Large Triangle as you are actually sorting all segments.although it's just a constant factor — in Java it is probably why it gets TLE.
I was actually somewhat close to the time limit before realizing I could cut my number of segments in half and making other constant factor optimizations, so I could see a Java solution timing out. However it was an unfortunate situation where a few O(n3) solutions were already getting through, so they couldn't afford to make the time limit much bigger. (Maybe n ≤ 3000 and 7-8 seconds?)
Yes, probably increasing n would make more sense.
Anyway, randomly discarding 20% segments makes my solution 42268118 passes. Probably because those are already covered by other segments.