Problem Authors: GT_18, karansiwach360
Author`s Code: 42406878
Code Complexity: O(LogN)
Problem Authors: csgocsgo, karansiwach360
Author`s Code: 42406891
Code Complexity: O(NLogN)
Problem Authors: csgocsgo, Ezio07
Author`s Code: 42406848
Code Complexity: O(N)
Problem Author: Ezio07
Author`s Code: 42406857
Code Complexity: O(NLogN)
Problem Authors: dhirajfx3, GT_18, TooDumbToWin
Author`s Code: 42406908
Code Complexity: O(NLogN)
Problem Authors: karansiwach360, hitman623
Author`s Code: 42406921
Code Complexity: O(N)
Problem Authors: 300iq
Author`s Code: 42406934
Code Complexity: O(262 * N + 26 * Q)
Problem Authors: dhirajfx3, DeshiBasara
Author`s Code: 42406942
Code Complexity: O(|x| * LogN * 26) per request.
We hope you enjoyed the problems!
Hope to see you all in next edition of Manthan.










Can someone tell me why i am getting this error in my code it is working fine in my compiler 42407188
your array should be initialized with a constant value. In case of your code: int a[n+1] and int si[l] are wrong!
Ezio07 It would be very helpful if you could add Time Complexity for all the proposed solutions. Thanks!
Yes, added!
another solution to problem A:
As was written, the answer it's number x for series of numbers: 1, 2, 4, 8,..2^x. This series of numbers it's geometric progression. The sum of the geometric progression is given by the formula: S(x) = (b(x)*q-b(1))/(q-1). For 1, 2, 4,..2^x q=2, b(1) = 1 and b(x) = 2^(x-1) => S(x) = (2^(x-1)*2-1)/(2-1) => S(x) = 2^x-1. The following condition must be met for the answer to be correct: S(x)<=n => 2^x-1<=n => n+1-2^x>=0. The code this solution: 42408562. (sorry for my not so good english)
Another solution :))
hey...can you explain me... how did u get this logic? thanku in advance @ Dragonol...
The logic is based from the binary form of n:
for exemple: n = 10. The binary form of 10 is 1010, you will need 1000,0100,0010,0001 to form any number x (1<=x<=10)
The answer is actually the length of binary form of n. In fact, log2(n) = length_of_binary_form_of_n — 1 so the answer shuould be log2(n)+1.
Thanks. Now I got it
Thank you for Explaination. I got it now
Hi,
I used cout<<(ll)(log(n)/log(2) + 1)<<'\n'; I got wrong answer. http://mirror.codeforces.com/contest/1037/standings/participant/19485663#p19485663 Can you please tell why?
Your code seems to be correct. Even ideone is giving the expected answer on 8 that is 4. https://ideone.com/tgBeiN
Yes, but codeforces is giving wrong answer.
GT_18 karansiwach360, can you please provide the reason?
It's clear case of precision error.
If you try
cout<<(log(n)/log(2)+1-4);, (for n=8) you'll get-1.60245e-016. On casting to (ll), the result you get is 3.///Deleted
loge(n)/loge(2) == log2(n), not loge(n-2).
Your solution sucks. If n could be up to 1018, it wouldn't work.
http://mirror.codeforces.com/contest/1037/submission/42365860
Yours fail too when n is up to 10^18, you suck.
That's because the problem condition for n is 1 ≤ n ≤ 10^9. If you want n up to 10^18, then here you are:
try to check n = 259 and n = 259 - 1
I don't understand . They both come out with 60. So i do the subtraction of 2^59 and 2^59-1, the answer is 0.Why?
most probably it's wshift-count-overflow try this
It also writes 60 for n = 259 - 1
but not for n=2^(59) do you have correct solution?
correct solution is to do all in integers. just go from 0 to 60 and check whether it is a right answer
32 - __builtin_clz(n)can anybody tell me why iam getting wa in test case 11 in D problem https://ideone.com/r2c4K5
A condition
2 2 1 1 2
output: Yes
this might be the condition
Can someone tell me D's solution? I read the D's tutorial and read other source codes, but I can't understand. What does D's tutorial say and what is the solution?
For understanding what the tutorial is trying to say, first you need to understand how graph is stored in an adjacency list and BFS Order Traversal. If you understand these two things, then you can read ahead.
Basically, the way you store nodes in adjacency list, determine how your BFS Order Traversal is going to look like.
So, for checking the given BFS Order, you store the neighbours of a node in the list according to the order they appear in the given BFS Order Traversal. Basically, "we can sort the adjacency lists of all the nodes in the order in which they are present in the input BFS Sequence." (as mentioned in editorial)
Once you get the adjacency list according to given BFS Order, Do BFS on the list and then check whether it matches the given order or not.
Here is my editorial to D. Let me know if it helps :)
42423685 oh Great minds think alike .
Can somebody tell me what is wrong with my code (42403836) for 4th problem.Actually I am getting WA on test case no.11 which is a large test case that is why I am not able to debug it.
maybe this condition
My answer is yes in this case what should be its answer?
Yes, you are right,answer should we yes
Thank you that helped me a lot !
see this comment
I submitted again, with little bit of moification -> (42416659) now it is passing the case you are pointing to,but still it is not passing the test case no.11
Can we do Problem D using Dijkstra's algorithm with edge weights set to 1 ?
Input order should be in increasing order of distances from the source.
If you ever use Dijkstra with all edge weights as 1, use BFS instead. But I don't think it would work. You have to add all nodes connected to the last node in some order, but you can't mix them with other nodes (even if they are on same distance from 1).
My submission for B is in queue for too long. 42412545 What should i do ?
Can someone tell me why i am getting this error in my code it is working fine in my compiler 42399951
You don't initialize local visited array with zeros
Can Someone Explain Problem B? Why are other elements modified when only the median needs to be modified?
Median is middle element in a sorted array.
Now, modifying Median may break the sorted order of the array elements. So we make sure elements before the median are still smaller than new median and all the elements after median are larger than new median too.
Still wondering: optimality proof for A, anyone?
Can anyone explain G more clearly?
For each character c, you need to precalculate grundy numbers of strings between consecutive occurrences of c, their prefixes and suffixes. When a string s breaks into multiple strings, the first part is a calculated suffix, last part is a calculated prefix. For other parts, you can keep prefix xor of the calculated xors. So suppose you have a string
adbecbdabfrand query ondbecbdabfand you choose characterb(as your first move), the precalculated grundy numbers will be ofad,ec,daandfrand their prefixes and suffixes. To answer the query, you takedsuffix fromadandfprefix fromfr.ecanddacan be retrieved from prefix xor.There are n + 26 such strings. You can consider them as queries while precalculating and order them properly such that the required values are calculated before the query.
Why actually "The best possible way to distribute the coins is to create packets with coins 1,2,4,…2k with maximum possible k such that 2⋅2k−1≤n. " is there any proof about that ? I have solved the problem and I still don't know why this happens!
To be able to make 1 you defnitely need the coin of value 1 so it has to be included.d now to make 2 you can include another coin of value one to sum to 2 or you can use a coin with value 2 so that you can make 3 as well so using coin with value 2 is optimal. You can go on inductively to show 2k is optimal.
Lets assume that we can take
<= log2(n)coins. We can choose some of them in2^log2(n) = ndifferent ways. So there are at mostndifferent sums. One of them is0. So we have at mostn-1non-zero sums. It is not enough to covernnumbers(1, ..., n). Thus answer is not<= log2(n), answer is>= log2(n)+1. So,log2(n)+1is optimal answer.Now we have to find
log2(n)+1coins. These are1, 2, 4, ..., 2^(log2(n)+1). We can prove its optimality by induction. Firsticoins cover numbers[1 ... 2^i-1]. Next coin is2^i. With that coin we can obtain also sums2^i, 2^i+1, ..., (2^i+2^i-1 = 2^(i+1)-1). So with firsti+1numbers we can cover2^(i+1)-1coins.I see that many people make arrays/vectors of size 2e5 + 5 if max number of elements is 2e5. Why is it not 2e5?
Maybe for work on boundary of array and taking this size to sure don't go out of size of array ... actually for more security
i see you have never got WA/RE because of wrong bounds
can anyone tell to me in task A why we can not do this with smaller number of packets?
Let me clarify problem E a bit, for current explanation goes more into details and less into the idea.
First, we build final graph of friendships. Then we delete from it all nodes with less than k friends — those buddies weren't going anywhere anyway.
The interesting observation is that all the remaining people can go to the trip on the last day. Now we can just play the time backwards. After we removed edge which appeared on day n and also all the nodes with friends number below k, all remaining nodes can go to the trip on (n-1)-th day. Then do the same thing for n-1, n-2, et cetera. Need to print results in reverse order though :)
Can you please describe how the third sample test case works??????? I couldn't figure it out.
Auto comment: topic has been updated by Ezio07 (previous revision, new revision, compare).
solved F with Divide & Conquer 42425616. Actually it's quite similar to the one in the editorial.
Why the code of E is so long......
Just have a look at the solve() function rest is just template.
Nice solution for E...
Will definitely give it a try
Problem F
Can someone push me in the right direction? I can't figure out how to get l and r for each element in linear time.
https://www.geeksforgeeks.org/the-stock-span-problem/
Thanks for help.
For problem F, Can anyone give an explain about how to calculate number of segment in [l, r]? Also, why the segment is not k, 2 * k — 1, 3 * k — 1 ... ?
Did you get the answer? I'm also confused why is it 2*k and not 2*k-1 in the explanation. EDIT: Got the answer. Here is a great explanation.
thanks, it's a good solution.
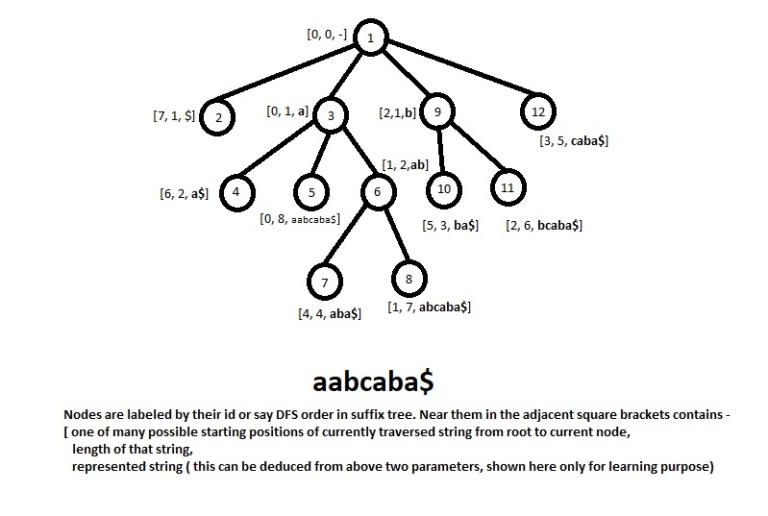
Could you explain, how did you solve the query part in O(|x|* LogN *26) per request? I solved it in O(|x| * LogN * LogN * 26) . I first build the suffix tree of given string. Then to find whether there is an element in range [l,r] in given subtree, I use binary search on each node of segment tree which are visited during query. Hence, there would be O(logN * logN) for each character (from 0 to 26) for each index of x in the worst case.
Consider of example the ith position of the array of leaves has value li, now we will be maintaining a set of persistent segment trees from left to right, that is persistent segment tree for ith leaf is obtained by adding value 1 to the li position of persistent segment tree of leaf i - 1. To do this, maintain three arrays, seg_tree, L_ptr, R_ptr. The node represented by integer id c will represent-
seg_tree[c]: The sum of values in the segment represented by current node.
L_ptr[c]: The left child of node represented by c.
R_ptr[c]: The right child of node represented by c.
Now to add the value li to the persistent segment tree of leaf i - 1 and get the root node for the persistent segment tree for leaf i, we can adopt the following algorithm.
If we have persistent segment of node i - 1 as c, we can obtain persistent segment tree for node i by calling add(c,0,|S|,li).
Now to find whether the current subtree contain any value in the range L ≤ R,
Let a + 1 be index of left-most leaf in the current subtree, and b be the right-most leaf in the current subtree and pj represent the persistent segment tree of leaf j.
Now we need to only take two segment trees pa and pb and query if sum of values in the segment L... R is non zero.
To do this we can apply the following method or say call find_sum(pa, pb, 0, |S|, L, R)
If returned value of the above function is non-zero then there is some value in the range L ... R. You may also like to see the find_first method in the code given in the tutorial to find the smallest value which is greater than L but less than R.
So this is how we can check in O(log|S|) time whether there is some leaf in the current subtree with value in range L ... R.
Let us know if something is still not clear.
Thanks :)
Может кто-то придумал решение на H с асимптотикой O(n * sqrt(n * log(n))) или лучше? За счет трика что уникальных длин около 400-500
Problem D. Test Case 39. Given Test Case - 2 1 2 2 1
My opinion —
Yes. But the checker saysNo. Can someone Explain to me why the answer isNo?You always start from root which is 1. So it's impossible that you visit any other node before 1. Therefore, sequence must always start with 1. Here it starts with 2.
If I have started at 1. Then because first no is 2. I would have printed no. But here the case is opposite. Checker is saying No, and I'm saying Yes.
In the given input, tree has two nodes. Root is 1, and it has single child which is 2. In this case, there's actually single BFS possible which is "1 2", not "2 1". You always start with 1. If first is not 1, then just print "No", no need to check anything else.
Then what does this mean ??
The BFS algorithm in this problem always starts with 1, however, it is not guaranteed that a[1] = 1.It means that correct BFS algorithm should start with 1, but we may give a sequence with a[1] != 1 which is necessarily an incorrect BFS sequence and you have to print "No" for such sequence.
Thanks. Got it. Was confused by the announcement.
Can you guys write the last part of the Problem F properly, more clearly?
hitman623
This is not clarification of the method from the tutorial, but slightly different method of calculating total count for each number.
On the figure above you can see progression of
barrays for given arrayaand k = 3. To calculate total count for number 8 you want to calculate count of all numbers in the triangle (their count is proportional to r - l) and then subtract blue ones (their count is proportional to i - l) and green ones (their count is proportional to r - i).Turns out, you don't really need all that case work. Here.
Yeah this is what we expect from the editorial that HOW it turns out that you don't need it.
Just do cout<<(long long)log2(n)+1 in Problem A
don't do that, please
About problem G. Editorial says we treat precalclulating like queries. So we iterate over character c and use two prefix/suffix dps and one range query. But yet we dont know grundy for each gap between two equal characters, we cant precalculate prefix xors. We can use segment tree, but than complexity becomes n*A*A*log(n) which is too long. So how to accomplish precalculation?
TooDumbToWin
Here is an O(n) solution to D :
42464470
Maybe this one is simpler :)
42377485
In problem D we need to check if the BFS sequence is valid or not. The editorial solution is really easy to understand. I guess same approach can be used if the problem was to check for valid DFS sequence.Only change would be that a DFS will be used instead of BFS. Can anyone confirm this, I am not 100% sure about it!
Yes, the editorial approach will work in that case also.
can anybody help me understand 1037E(Trips) problem??
See this explanation from saluev
Can anyone explain the E question clearly? I dont get the author's logic
For D, I made an array
par, for which,par[i]=jmeans thatjis the parent of the node numberedi. I constructed a queue,Qthat is used to imitate the BFS. Now, I add the current node (first node initially) to the queue, and check whether the nextknodes (wherekis the size of the adjancency list for the current node) have the current node as their parent, while adding these nodes to the queueQ. After theseknodes are checked, I remove the current node from the queue.This will work for any order of neighbor selection for the BFS. The submission can be found here. It doesn't work for the test case 12. Any ideas? I think the implementation is correct, but there is some problem with the concept.
We can perform Problem D in $$$O(n)$$$ using two-pointers.
80832291
Aren't you using a vector<set<>> ? So time complexity can't be O(n). Shouldn't it be O(nlogn)? I'm not sure of my answer though
Actually I never end up using
vector<set<int>>>after initialising... so you can just remove that part of code and it will be $$$O(n)$$$