→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
→ Find user
→ Recent actions
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Dec/22/2024 14:59:56 (l1).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|










Can someone elaborate how to solve the third subtask in seats problem.
3. (20 points) H <= 1000, W <= 1000, Q <= 5000Thanks in advance.
My approach: Let Bk be the bounding box of all numbers from 1 to k.
If area(Bk) = k, then Bk is beautiful. Conversely, if R is a beautiful rectangle and area(R) = k, then area(Bk) = k. And finally, if area(Bk) = k, then area(Bk + 1) > k, because if R = Bk is beautiful, then either Rk + 1 or Ck + 1 is outside of the bounding box Bk. Without loss of generality let it be Rk + 1. It follows that k + 1 is the first contestant at row Rk + 1.
So, all we need to remember is the contestant with the lowest id that is in the row i, and the contestant with the lowest id that is in the column j. We can do this by simply maintaining an ordered set of the indices of contestants for each row and column. This can be maintained in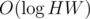 per query. Using this, we obtain H + W candidates on the beautiful rectangles in O(H + W) time and we simply check all of them.
per query. Using this, we obtain H + W candidates on the beautiful rectangles in O(H + W) time and we simply check all of them.
To check a candidate for a rectangle, we have a segment tree for calculating the minimum/maximum row/column on a range. This gives us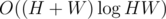 time algorithm to process one query.
time algorithm to process one query.
Combined together, this is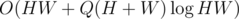 .
.
To check a candidate for a rectangle, we have a segment tree for calculating the minimum/maximum row/column on a range. -> we can improve it to O(H+W) easily. (update r1, r2, c1, c2). Overall time complexity is O(HW + Q(H+W)).
Can you explain more on how it can be improved?
Would 10^7 segtree operations really pass?
My solution involves just iterating all the positions and recomputing for each query. You will get a total of 37 points with this.
Lets define a beautiful box Bk as a box containing only numbers 0 to k-1 I would sore in array
arr[id] = {r, c}the position of each contestant. Then for a bounding box Bk to exist the prefixarr[0..k]should form a rectangle. For that I get the min/max for column/row in the prefix of sizekand check if the rectangle is exactly of areak. If yes then that is one box. So I compute this in O(HW) and build an array stating if Bk is a bounding box or not. When each query arrives I will update positionsaandband recompute the positions of the array in the rangeaandbin O(|a - b|).how can this pass in TL ? isnt it O(q*HW) ?
THe thing is you first do $$$O(HW)$$$ to compute all good prefixes (the ones which form a rectangle) when you do a swap $$$O(|a-b|)$$$ only $$$10,000$$$ prefixes can change and hence you only need to check those to update your total count of good prefixes and answer the query.
I am talking about the 20pnts stask. there, the (|a-b|) = 10K constraint was not there.
Oh, I see. It is right it doesnt work for the 20pts, I might have missed that. For the 20 points the number of rectangles is less than 4000 and you can compute them iteratively starting from the 1x1 rectangle and then expanding it to include the [MEX](https://en.wikipedia.org/wiki/Mex_(mathematics)) of the current rectangle. For that you only need to have the MIN in each column and each row which can be updated on every update.
Someone help me problem werewolf :D . I don't have any idea about this problem
Read the editorial at the official IOI website.
LooOoOoOOOooOoLooOooOooOooL. LMAO. ROFL.
Are you even too lazy to google that?
nopeeeee. i attemp many times but i don't find :D
I tried solving the fifth subtask of the problem seats (H = 1), but after reading the editorial I cannot understand how to use the lazy propagation segment tree to solve this. Can someone explain little bit on how to do this. Thanks in advance.
I can try this but I'm not sure if it is correct. Let's color cells which contains numbers 1 — x black others are white. Condition for this to be beautiful rectangle is that the (number of white cells which are adjacent to black cells should be <= 2). We have to maintain this value for each prefix.
Building : Let current number be 'x' and its position be 'pos'. Consider three case — both neighbour cells are black or one of them is black or none of them is black. For 1st case subtract 2. For 2nd case do nothing. For 3rd case add 2 to prefix 1-x.
Updates : Let two values that are swapped are 'sm' and 'lg'. sm is smaller of them. Consider 'sm' cell. Let its initial neighbours be val_11, val_12. If val_11 is greater than 'sm' subtract 1 from prefix(1,val_11). Same of val_12. Let its final neighbours be val_21, val_22. If they are greater than 'sm' add +1 to their prefixes. Do the same for larger value 'lg'. Update prefix (1-sm) & (1-lg) seperately.
Query : Check how many prefixes follow to above condition. You can easily check necessity and sufficiency of the condition.
Thank you for your reply, just to ask, in your update function by val_11 and val_12 do you mean the left and right neighbours of the current position?
Yes.
Can someone write editorial of day1 problem A please!