Sereja's blog

Codeforces Round #156 tutorial
By Sereja, 12 years ago, translation, In English

255A - Greg's Workout

It is not hard problem. We must calculate sums of numbers for each group and print group with maximum count.

255B - Code Parsing

Not hard to see that after few operations of first type string will become: x..xy..y. After fer operations of second type, there will be only letters of one type, count of this letters will be: |count(x) — count(y)|

256A - Almost Arithmetical Progression

Заметим, что ответ это длина последовательности: a, b, a, b, ... где a и b — некоторые целые числа. Зафиксируем одно число (допустим a), будем перебирать число b, и считать какой мы получим ответ, если это будет последнее число в последовательности. Заметим, что для фиксированных a, b — ответ считается жадно. Так же будем действовать и тут. Будем искать последнее вхождение числа b до зафиксированного, что между ними есть число a, и будем брать ответ как длина до найденного числа +2 (икасть будем с помощью метода двух указателей). Так же нужно рассмотреть случай, когда это будет 1е или 2е вхождение в последовательность.
Так же существует решение с помощью динамического программирования.
Асимптотика обоих решений O(n^2).
Буду очень рад, если кто то напишет решение с лучшей асимптотикой.

256B - Mr. Bender and Square

Solution — binary search for answer. Next we have to calculate the area of a truncated square set at 45 degrees. This can be done as follows: Calculate its total area. Subtract area that cuts off the top line. Similarly, for the lower, left and right line. Add parts that are cutted by corners. You can write a function that finds the length of the truncation desired area, for that would not write a lot of code.

256C - Furlo and Rublo and Game

Note that after the first move any pile turns into a pile no larger than 1000000. We assume Grundy function for numbers less than 1 million. Grundy function is very small, you can start on the partial sums for each type of function that would quickly tell what function is in the interval, and which are not present. Knowing the answer is not difficult to find small response for all piles.

256D - Liars and Serge

If person say number x, and at all x was said by x persons, then we cannot tell anything about fixed person.

Now we understand which sequence are good for us. We will calculate their count wuth dynamic programming dp[n][m][k], n — which persons answers we set to the sequence right now, m — how mant persons gived theis answers, k — how many persons from them are liers.
Transfer:
dp[n][m][k]*cnk[N-m][n] -> dp[n+1][m+n][k]
dp[n][m][k]*cnk[N-m][p] -> dp[n+1][m+p][k+p] p = 1 .. N, p != n.
We assume, that N — total number of the persons. This solution get TLE, becouse complexity if O(N^4). We need to use precalc. It will not be so big, as N is power of 2.

256E - Lucky Arrays

Solution is — interval tree. We will save dynamic programming f[i,j] in each vertex, this dp means: in how many ways we can change all 0 to some numbers on interval, such that it will be valid and first element will be i and last will be j.

With normal implementation its easy to pass system tests.

  • Vote: I like it
  • +22
  • Vote: I do not like it

Comments Comments (25)
| Write comment?
»
12 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Can you translate tutorial for Div2 C also, please? Or if someone else could give a detailed explanation I would be thankful :)

→ Reply
  • »
    »
    12 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    One solution that pass system test.

    Note that the task actually asks about the longest subsequence in the form a, b, a, b, a, b, ..., and we can do the following.

    First normalize the elements into ranks when they are sorted. e.g.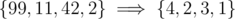 . Then define a function fi, r be the longest subsequence obtained ending at the i-th element, and the previous element is of rank r. Define fi, 0 = 1 for all i, being the base case. Then one can derive the following transition:

    where rj is the rank of the j-th element. Since there are O(n) different ranks, using DP the algorithm takes O(n2) time to compute all fi, r. Pick the largest among them as the answer.

    → Reply
  • »
    »
    4 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    A Detailed Explanation Indeed !

    → Reply
»
12 years ago, # |
  Vote: I like it +6 Vote: I do not like it

problem "256A — Almost Arithmetical Progression" is in Russian. Dose it have English editorial?

→ Reply
  • »
    »
    12 years ago, # ^ |
    ← Rev. 4   Vote: I like it +1 Vote: I do not like it

    this is my idea :

    define dp[i][j] = maximum length of subsequence of sequence of b that two first element of it would be equal to b_i and b_j

    dp[0][0] = 1 and dp[i][j] = 1 + dp[j][k] (k is last element that is b_k is equal to b_i)

    the only problem is to find k for every i and j that can be solved easy by make a vector for every b_i values of indexes for every b_i (1<=b_i<=1000000) and binary search ...

    code : 2785803

    → Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    DP solution for 256A

    → Reply
»
12 years ago, # |
  Vote: I like it -18 Vote: I do not like it

→ Reply
»
12 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Your tutorial is as well as your problems , tnx

→ Reply
»
12 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Thanks for the editorial! However, could you please translate the explanation for problem C Div2 into English? Thank you.

→ Reply
»
12 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Thought this might help

Translated version of Div2 Prob C:

Note that the answer is the length of the sequence: a, b, a, b, ... where a and b — integers. We fix one number (say a), will sort out the number of b, and consider what we get a response, if it is the last number in the sequence. Note that for fixed a, b ​​- the answer is greedy. So are we going to act and there. We look for the last occurrence of b fixed to that between them is the number of a, and we will take the length of the response to the found number +2 (Ikast be using the two pointers). As it is necessary to consider the case when it is 1st or 2nd occurrence in sequence.

There is also a solution using dynamic programming.

Asymptotics of both solutions O (n ^ 2).

I would be very happy if someone would write a better solution with asymptotics.

Credits: translate.google.com

→ Reply
»
9 years ago, # |
  Vote: I like it +5 Vote: I do not like it

A "brute-force" solution for 256A — Almost Arithmetical Progression.

The problem asks to compute the length of the longest subsequence in the form of a, b, a, b, ....

Let A[1..n] denote the origin array. One easy observation is that the value of each A[i] is not important, and thus, we can map each A[i] to the range [1, n] accordingly. Let pos[i] contain all indices of number i in A. For example, A = [3, 2, 2, 1, 3, 2], then pos[1] = [4], pos[2] = [2, 3, 6], pos[3] = [1, 5].

If a = b in the optimal subsequence, the answer is just max(pos[i].length). Otherwise, we enumerate all pairs of (a, b), where a ≠ b, and computing the longest subsequence, when both a and b are fixed, can be done efficiently by merge-sort. (Note that, all pos[i]'s are already in sorted order.) It then remains to analyze the total runtime of this procedure. There are at most n unique keys for pos[i], so O(n2) time for enumerating all pairs of a, b. Plus all the mergesorts, it seems like the overall runtime is O(n3). Fortunately, it is not the case, and a tighter bound is O(n2). Why?

If we do a more careful analysis, the total runtime is bound by

Therefore, the problem can be solved by brute-force in O(n2) time using linear space.

→ Reply
  • »
    »
    8 years ago, # ^ |
    ← Rev. 4   Vote: I like it 0 Vote: I do not like it

    Suppose there are k unique values.

    for i = 1 to k

    for j = 1 to k

       calculate(i, j) => this should be done in |b(i)| + |b(j)| operations using two pointers

    then for j loop, total operations would be

    |b(i)| + |b(1)|

    |b(i)| + |b(2)|

    .

    .

    |b(i)| + |b(k)|

    so total would be k * |b(i)| + n (right column sums to total values n)

    now doing similar for the outer loop

    k*|b(1)| + n

    k*|b(2)| + n

    .

    .

    . k*|b(n)| + n

    Adding all columns, total operations would be k * n + n * k = 2 * n * k = O(nk) where k is the total number of unique values. since k <= n this O(n^2) is achieved

    → Reply
»
8 years ago, # |
  Vote: I like it 0 Vote: I do not like it

DP Solution for 256A
As others have already pointed out, you can map A[1..n] values to 0..n-1
Once, the values are mapped, fill an array dp[i][j] which contains the max subsequence length ending with i and previous element being j.

Initialize: dp[i][j] = 1
for i = 1..n
    for j = 1..i
	d[i][a[j]] = max(1 + d[j][a[i]], d[i][a[j]]);

max over all d[i][j] is answer.

21394975 is my Accepted code

→ Reply
  • »
    »
    8 years ago, # ^ |
      Vote: I like it +4 Vote: I do not like it

    I tried really hard to implement this DP with a top-down recursive function, but I failed... Can you please help me with that? Thanks!

    → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +4 Vote: I do not like it

      Here you go 23015907 :)
      Needed to do some additional preprocessing to get it within timelimit.

      → Reply
      • »
        »
        »
        »
        8 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Do you think it's possible to achieve n^2 with a recursive solution? This situation is really impressive to me... I thought that all bottom-up DPs had a top-down version with at least the same time complexity... Knapsack/Bellman-Ford/Floyd-Warshall are all DPs that need more space when implemented recursively, but they have the same time complexity! =(

        → Reply
        • »
          »
          »
          »
          »
          8 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          I'm not really sure. There might be a n^2 solution but I'm unable to think of one.

          → Reply
    • »
      »
      »
      8 years ago, # ^ |
        Vote: I like it +1 Vote: I do not like it

      Also, it is worth noting that none of the top 30 div-1 folks used Top-Down approach. I read people are generally worried about stack-overflow due to too many function calls. Check pros and cons section in http://stackoverflow.com/a/6165124

      → Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

A detailed DP Approach for 256A

I found the editorial and and other comments' quite complex. I tried to explain the same approach in a bit simple way.

We have to find the longest subsequence of A,B,A,B,A,B,... Type. Since in an array of size n, we cant have more than n different numbers, we map the numbers accordingly. For example, a = [ 10 , 20 , 30 , 20 , 30 ] --> a = [ 0 , 1 , 2 , 1 , 2 ] We updated the initial array!

Now we create dp[n][n], where dp[ i ][ j ] means length of longest subsequence ending at i th element (a[ i ]) and j th element (a[j]) being the previous element in subsequence! Here's the tricky part: For every (i,j) , we dont update dp[ i ][ j ], Instead we update dp[ i ][ a[ j ] ]. (Yes, some dp[ i ][ j ] may never be updated , if array elements repeat , but we just have to find the maximum length. It'll make sense soon! )

Initialize: dp[ i ][ j ]=1 for all i,j possible. 

for all i = 1..n
    for j = 1..i
        dp[ i ][ a[ j ] ] = max(1 + dp[ j ][ a [ i ] ], dp[ i ][ a[ j ] ]);

Consider the following example.

a = [ 10 , 20 , 30 , 20 , 30 ] . We Updated it to -> a = [ 0 , 1 , 2 , 1 , 2 ]

DP Table would look like: 

 1 1 1 1 1 
 2 1 1 1 1 
 2 2 1 1 1 
 2 2 3 1 1 
 2 4 2 1 1

(0 based indexing). Array a=[0,1,2,1,2]

See the cases when i=4,j=1 And when i=4,j=3.

In DP Table Creation:

When i=4,j=1: dp[4][1] = max( 1 + dp[1][2] , dp[4][2] ) = max(1+1,1) = 2

When i=4,j=3: dp[4][1] = max( 1 + dp[3][2] , dp[4][2] ) = max(1+3,2) = 4

Observe:

See when i=4 , j=1 it means last element of sequence is "2" and 2nd last element of sequence is "1" , where "2" is the 4th element of a[] and "1" is 1st element of a[].

And when i=4 , j=3 it means last element of sequence is "2" and 2nd last element of sequence is "1" , where "2" is the 4th element of a[] and "1" is 3rd element of a[].

In both these above cases we updated dp[4][1] only. We never update dp[4][3].

dp[4][1] is Our answer means sequence is max. when it ends at 4th element and the value at 1st element is same as the 2nd last sequence element, but it not necessary that 1st element only is the 2nd last element in sequence !

There is a tricky difference here. Observe that 1st element is not the 2nd last element in sequence. But the value of 1st element is the 2nd last element in sequence, is what is defined by dp[4][1] !

My Code

This was truely one of the most beautiful DP Question! (And I feel worth 1800 maybe?! )

→ Reply
»
4 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Can anyone please help me with this submission of 256A? I can't figure out what's wrong with it. https://mirror.codeforces.com/contest/255/submission/83326327

UPD: found the error (Sorry).

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Div 2 Problem C LINK

→ Reply
»
4 years ago, # |
  Vote: I like it 0 Vote: I do not like it

i know i am late.

but i could not understand why i am getting wrong ans on test case 22.

help is very much appreciated

my code

→ Reply
  • »
    »
    3 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    idk if you still need any help but try testing for this test case: 4 1 1 1 1 if you get 1 as ans then it's wrong, the answer should be 4.

    since p can also be zero.

    → Reply