You are given an array A of first n natural numbers (1 to n). We say two numbers x and y are connected if gcd(x,y) >= t where t is some given threshold.
You are given query arrays source and destination of the same length. You need to find for every i, whether it is possible to reach from source[i] to destination[i] for the given constraints.
Example: n = 6 A = [1,2,3,4,5,6]
source = [1,2,2]
destination = [6,3,6]
threshold = 2
answer = [no,yes,yes]
Solution:
When we draw the graph, we have:
1 is not connected to anybody since threshold is 2.
6 is connected to 2 and 3 since gcd(6,3) = 3 and gcd(6,2) = 2.
So even 2 and 3 are connected indirectly.
Expected time complexity: As good as you can get. I would be glad to know as many approaches possible even if they have bad complexities.










How large is n ?
No fixed value. Its only about getting a good solution. I was thinking n*log(n) would be a very good place to be.
Discard all numbers less than t. Compress equal numbers in the same component. A component will represent several indices from A. Iterate i ≥ t and find a list of all nodes which are multiples of i. Suppose you get P nodes, add P - 1 edges to connect them. After, find the connected components and mark every index of A with its corresponding component id. On a query, check if the ids match.
Start from x = t to n, and connect all multiples of x using a dsu. For query simply check dsu for same connected component. Complexity O(k*(nlogn+q)) where q is the number of queries, and k=logn or inverse ackerman, depending on how you build the dsu.
You probably get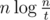 rather than
rather than 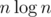 , since you exclude x = 1 to t-1, right? I know it doesn't make a big difference, but it's a bit of a tighter bound.
, since you exclude x = 1 to t-1, right? I know it doesn't make a big difference, but it's a bit of a tighter bound.
Yeah you're right, it'a a tighter and more accurate bound, but it's better to always think in terms of worst case scenario.