Please help on this problem:
We denote the function F by:
\begin{cases} F(x) = 1 & x\leq 2 \\ F(x) = F(x — 1) + F(x — 2) + x & x > 2 \end{cases}
Given q (1 ≤ q ≤ 105) queries. The queries are characterized by two numbers l, r (1 ≤ l ≤ r ≤ 109). Find: 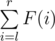










substitute F(x) = T(x) + ax + b, and equate coefficient of x and constant term to zero to get T(x) = T(x - 1) + T(x - 2) which is just fibonacci sequence, btw (a, b) = (-1, -3) in this case
This particular problem can be solved in many ways, one of them is already mentioned.
In general, try to define new functions other than the given one in the problem, and try to define the whole system of functions in terms of recurrences in terms of each other, and finally do matrix exponentiation. I'll try to explain through this example.
Let pre(x) = pre(x-1) + f(x)
So, your answer is pre(r) — pre(l-1)
f(x) = f(x-1) + f(x-2) + x
Since we don't know what to do with x, define a new function g(x) = x
f(x) = f(x-1) + f(x-2) + g(x)
Now try to define recurrence for g(x)
g(x) = g(x-1) + 1
Again, we don't know what to do with 1, let's define h(x) = 1
g(x) = g(x-1) + h(x)
Try to define recurrence for h(x)
h(x) = h(x-1)
Now, you can easily build a matrix for pre,f,g and h, and do exponentiation to get your answer
This is so awesome... Never knew that.
Btw do you know some medium-hard problems involving this?
I don't remember many, but these 2 come to mind.
https://www.hackerrank.com/contests/infinitum14/challenges/mutual-recurrences
https://www.spoj.com/problems/PIBO/