Let's discuss solution
→ Pay attention
→ Top rated
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
→ Top contributors
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | awoo | 154 |
| 8 | Dominater069 | 154 |
| 10 | luogu_official | 150 |
→ Find user
→ Recent actions
↑
↓
Codeforces (c) Copyright 2010-2024 Mike Mirzayanov
The only programming contests Web 2.0 platform
Server time: Dec/22/2024 10:54:36 (j2).
Desktop version, switch to mobile version.
Supported by
User lists


| Name |
|---|











How to solve D?
For D, we did a matrix exponentiation on number of different graphs (for n=5, there were only 34 different graphs, link). However, it was still somewhat slow to raise power for every query and precomputing "power of 2" matrices was not enough. So the idea was instead of doing (A(B(CD)))v we did (A(B(C(Dv)))) which is qlogn*n^2 instead of qlogn*n^3. And that was sufficient to get AC (My teammate Bruteforceman mentioned this blog).
You can normalize each state. Then for n=5 there only remain 34 states, 13 of which are unconnected. If you know the probability distribution of states at time l, you can use matrix exponentiation to get the answer, since 143·q·log(r - l) fits within the time limit (one extra state for 'having been in any connected state').
Unfortunately 343·q·log(l) seems too slow to use matrix exponentiation directly for getting this probability distribution. Instead, using matrix exponentiation again, calculate the probability of exactly k edges flipping in l steps (only 11 states so it again fits within the time limit). Now iterate over the (unnormalized) state at l and using previous result it is relatively straightforward to compute the probability that this will be the state at l.
Combining these two steps got me AC in 373ms.
Can you elaborate: <<calculate the probability of exactly k edges flipping in l steps (only 11 states so it again fits within the time limit)>>?
Don't you need to know the exact edges? Or it's like, for each bitmask of edges, you check what's the probability only these will flip?
If you want to go from one state to another state, you know how many edges should flip and using the matrix exponentiation you get to know the probability of exactly this many edges flipping. To get the probability of this specific set of edges flipping, divide by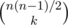 , since each set of edges of the same size has the same probability of being flipped.
, since each set of edges of the same size has the same probability of being flipped.
Could you elaborate how to maintain the "extra state for having been in any connected state"?
How to solve E?
Generate a million binary strings and pray.
Solved by Bruteforceman. The main idea is: suppose you would like to know what is at i'th position. Then query for:
and so on. Say the reply to the first query is X and to the second query is Y. Now, the probability for both being valid is 1/4. Also, you may assume that if: Y = {X, X-1} then may be (X, Y) are valid. So record, X-Y. If you see number of 0 or 1 going over say 2 or 3, then you know that by high probability the answer is that number (0 or 1).
Is there any proof for probability bound in this solution? I think the chance of getting AC in one try is quite low, considering that there were 150 test cases :(
It's important to use long intervals: When i < 500, use [i, 1000], [i, 999], ..., and when i > 500, use [1, i], [2, i], ....
That is exactly what I submitted, but got WA..
Same. Got WA on test 33.
Waiting for 4 evidences accumulating either to the side of 0 or to the side of 1 was enough to get AC (but 3 is still not enough, 5 is also OK and 6 exceed the query limit).
UPD This is wrong as pointed by pavel.savchenkov below (I also locally stress tested the solution and achieved the same results).
UPD 2 Interestingly enough, I also made a mistake when accounting for query caching. Actually it is not so wrong, at least for 4 (but 5 already exceeds query limit and 3 sometimes identifies the string incorrectly).
Code: https://pastebin.com/xHKKWFSX Said code passes 1000 random tests with less than 17000 queries used on each. Note that linked code does not ask queries till the end of the string, but rather on substrings of length ≈ 400.
UPD 4 Removed all statements about weak tests, actually it was just me counting queries incorrectly.
For waiting for 4 evidences you need ≈ 31950 queries according to my local stress test. Indeed for each 0 ≤ i < 1000 you need to wait for 4 appearances of event with probability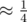 . So average waiting time is
. So average waiting time is 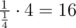 . 2 queries for each step and we get 1000·16·2 = 32000. So even 32000 should not be enough.
. 2 queries for each step and we get 1000·16·2 = 32000. So even 32000 should not be enough.
To get the i-th position you call [i, 1000], [i, 999], ... and [i + 1, 1000], [i + 1, 999], .... Then to get the i + 1-th position you call [i + 1, 1000], [i + 1, 999], ... and [i + 2, 1000], [i + 2, 999], .... This means that many queries can be shared and the number of queries is roughly halved.
Thanks, that's a good point. It was stupid, I forgot to cache queries in local test, did it only in server version. But I still getting ~ 18700 queries.
Wait until the difference of number of evidences becomes 3. In each attempt you get a correct one with probability 1 / 4, and a wrong one with probability 1 / 1000. This means that the failure probability for a single position is about (1 / 250)3 and the failure probability is about 1 / 15625. https://ideone.com/jOqZgM
Let
DP[a][b]be the probability that we succed if we're waiting for a pieces of good evidence or b pieces of bad evidence. With a single query, we either get good or bad evidence or nothing. Let pg be the probability of getting good evidence and pb the probability of getting bad evidence. ThenBy a union bound, the probability to fail at all is at most 1000 times the probability to fail at any point, so 1000·(1 - DP[n][n]).
So it seems like waiting for 2 pieces of evidence is not enough, but waiting for 3 pieces should work at least half of the time if we assume 250 test cases (by another union bound).
The solution where you wait for a difference of at least 3 should be evaluatable with a Markov chain instead of DP. I might do this after dinner.
Edit: Markov chain code. Table:
So here n = 3 works at least 95% of the time if we assume 250 test cases.
Our solution which passed stress testing:
Let's guess the second half of the string. For each ask for K values: [0, r], [1, r], ..., [K - 1, r]. For each
ask for K values: [0, r], [1, r], ..., [K - 1, r]. For each 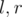 consider multiset
consider multiset 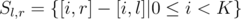 . Sort all pairs by decreasing of frequency of the most frequent value in
. Sort all pairs by decreasing of frequency of the most frequent value in 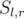 .
.
Now we found some correct differences of some prefix sums. So go through these pairs in sorted order and join indices in DSU (like in Kruskal's algorithm) until we got components. To get remaining
components. To get remaining  edges just ask for value in some positions, like in other solutions waiting for 4 evidences. Then do dfs on generated tree and find out all
edges just ask for value in some positions, like in other solutions waiting for 4 evidences. Then do dfs on generated tree and find out all 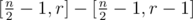 .
.
We used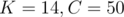 .
.
Let me summarize the solution for E. Many people are downvoting descriptions of solutions, but they are correct and I have a complete proof for it. However, various details are important in the proof and slight difference of algorithm may result in significant difference of number of queries / failure probability.
We decide letters one by one. Basically, to decide the i-th letter, we choose some j, and compute the difference of [i, j] and [i + 1, j]. For a single choice of j, it returns the correct answer with probability at least 1 / 4. So, if we repeat this for various j and get some statistics, it's likely that we get the correct value of si.
Suppose that si = 0. As we see above, for any j, the probability that we get the evidence of si = 0 (i.e., Query[i, j] = Query[i + 1, j]) is 1 / 4. What is the probability that we get the evidence of the opposite thing (i.e., accidentally get Query[i, j] - Query[i + 1, j] = 1)? To keep this probability small, it's important to use long intervals. When j - i ≥ 500, this probability turns out to be about 1 / 1000 (by a simple calculation). There's no such j when i is big, in this case we should use Query[j, i] - Query[j, i - 1] for some j.
Since this is probabilistic, we need to try various js. How many js should we try in particular? Imagine a lottery that gives one of "A" or "B" with probability 1 / 4, the other letter with probability 1 / 1000, and "?" in all other cases. We want to decide which of "A" and "B" is more frequent by drawing this lottery several times. One natural way is to repeat drawing the lottery until the difference between (the number of "A"s) and (the number of "B"s) becomes 3. Again, some computation shows that with this strategy, we can almost always find the correct one: the failure probability is about (1 / 250)3. (This is equivalent to Gambler's ruin. See the section "Unfair coin flipping"). Note that, another natural way is to stop when you get the same letter three times: it has a worse error probability.
If we use the strategy above for all positions, since in each position we fail with probability (1 / 250)3, the total failire probability per testcase is about 1000 * (1 / 250)3 = 1 / 15625. Thus this algorithm will get AC with about 99% probability even with 150 testcases.
What is the number of queries? Again, the detail of the choice of j matters. One possible way is to use j = 1000, 999, 998, ... when j < 500 and use j = 0, 1, 2, ... otherwise. For a single i, we draw the lottery about 12 times on average. This is because in 12 attempts the expected difference between the number of two letters is about 3. Thus, for small i, we send queries for intervals [i, 1000], [i, 999], ..., [i, 989] and for large i, we send queries for [0, i], ..., [11, i]. Note that, when we try to get si we use queries [i, j] and [i + 1, j], and when we try to get si + 1 we use queries [i + 1, j] and [i + 2, j]. We should memoize the answer for [i + 1, j] and do not ask it multiple times. In total, roughly speaking, we need 12000 queries on average. Of course, the number of attempts for a single i is not always exactly 12 because this is a probabilistic parameter. This raises the number of queries a bit, but still we are comfortable with the limit of 18000.
My code: https://ideone.com/jOqZgM
I'm the author of this problem and I understand that I failed and set too low query limit.
We had too much problems with contest preparation and I asked my team to solve problem E and write solution that you described. Their solution has different constant 6 and uses not more than 18000 queries. But only after contest I realized that they use some optimization. The solution only asks segments with length up to 500. So almost every segment is used four times.
We didn't think about reusing queries, so we came up with an approach that requires less queries. First, for the first BUBEN numbers, do your solution, but without any memorization (I think we had BUBEN=300). This does on the order of 24 queries per item as you describe. Then, when we know all numbers from 0 to i-th, we can ask queries [j, i+1] to determine (i+1)-th number, since we know the sum in segment [j, i] already. So now we have probability of success 1/2 instead of 1/4, and for each attempt we need 1 query instead of 2. The segments are a bit shorter, though, so to be safe we waited for 5 votes here.
How to solve F, G, H?
My solution for F: Let's build the sorted list of the players one by one. To find the correct position for the next player we use binary search. That gives us 1000 * log operations which is about what we need.
Now the question is how to compare two players in the binary search? We have 5 groups: higher then 1st, 1st, 2nd, 3rd, lower then 3rd. Let's take any 2 people and ask if one is lower than the other. If we have no answer then we swap them and ask again. You can see that only for (1st, 2nd) and for (1st, 3rd) that will not give you the order. For others you will have the answer and complete the binary search iteration. If during the binary search we failed to insert the element, let's save it for later.
Now in the end we have one or two saved elements and the sorted list. I iterate from the lowest to highest asking the order and that's how we can find 1st-3rd person in the list. Then insert our saved for later there in any order and just sort those 3. That is easy — ask all 6 questions and it's enough to find the order.
I liked the problem personally, really nice. Kudos to the author.
Wow, this sorting algorithm is faster than merge sort. Only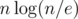 comparisons instead of
comparisons instead of 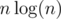 ! I solved it with mergesort and thought that this problem is just about casework. Really nice that it has such an awesome solution.
! I solved it with mergesort and thought that this problem is just about casework. Really nice that it has such an awesome solution.
My solution: Pick a guy, let's call him zero. Ask zero about everyone, and everyone about zero. This way, you know whether zero guy is first, second, third (I call these medal guys), above first or below third. Furthermore, you know the categorisation of all the remaining guys (except that sometimes you cannot distinguish a medal guy from either above or below guys). Write quicksort to sort the above and below guys. For the medal guys, you sometimes need special handling:
Then it's fairly standard:
I have a simmilar soluton, but we I pick the pivot I only ask the pivot about everyone and not also everyone about the pivot. It requires some extra casework. I actually had a bug in a very special case. And it didn't always work even on the sample but it was so rare I decieded to submit. Firsr submir, WA on 49. Submit the exact same code once more because the solution is randomized, AC :D.
G: When deciding where to move, try the following in order (r is some value depending on your dice, described below.)
As for dice selection, there are a few possible issues
Two dice dice selection strategies that work:
(I ignored the time taken to get the dice in my analysis, should be around 1'000 for the first and 7'000 for the second strategy in total, but the influence of this is halved as we're already moving toward (0, 0) during this time.)
In the middle of the contest after 2 WAs on E our team decided to open pdf statements and found out that there is query limit in all interactive problems. :(
I stared for ages at why my codes for E and F gave wrong answer. I just found out that there is a query limit, which was not mentioned in the 'one-by-one' problem statement, but was only mentioned in the pdf which you can get by clicking on 'download statements'.
To be honest, I found it kind of strange that there was no query limit, so I read the statement (many times) letter for letter, but did not think to look in the pdf. Well, now I now better for next time.
How to solve A?
First the slow solution:
If you think a bit, you will be able to optimize the solution. First of all, set_of_taken_digits is a 10 digit bitmask. So, we will store dp[i] for each 0 <= i < len(S) where dp[i] is a 2^10 length array storing dp value for each bitmasks.
To compute dp[pos], we need dp[pos-1] (for the second if) and sum of dp[i] where S[i — 1] == S[pos]. So, we only need two 2^10 array (dp of i-1, and dp of i) and 10 2^10 arrays (for each digit).
Does somebody know whether div2 upsolving is already enabled?
Div.2 problem I was the easiest one. To compose lexicographically minimal string of zeroes and ones with given occurrences of '00' .. '11'. First idea was to write code with many "if ... else ...". Later I tried to partly bruteforce (--> spoiler). But what was the most simply or most elegant solution?
Need to find out some rules: 1) answer string can not contain more than one substring of repetitive zeroes or ones, otherwise you could move at least one digit from one such a substring to another to make new string lexicographically smaller; 2) difference between occurrences of '10' and '01' can not exceed 1.
And idea was to minimize (simplify) occurrences, generate a range of binary strings and sort them, and then find the first string which contain exact numbers of minimized occurrences. Finally, expand this string to original occurrences.
I minimized occurrences of '0' and '1' to <= 1, and minimized occurrences of '10' and '01' so that the maximum is 2, but difference is preserved.
To generate binary strings 0 .. 2^16 and multiply this set by 3 prepending different numbers of zeroes (0 .. 2) to each string.
Match simplified occurrences onto strings. Expand first matched string by: '10' -> '1010' x times by difference between minimized and original occ. of '10' ('01'); same with '0' -> '00' (from the beginning of the string); and same with '1' -> '11' (from the end of the string).
How to solve C K and L?
how to solve K?
UPD: wrong post