GP of Spb 2018-2019 - Codeforces

6 years ago, # ^ |

+41

E: I used Java Biginteger since the numbers were too big.

We can represent the points on the first segment as parameter of t. If A and B are vector to the two end points, then an arbitrary point on AB is: tA + (1-t)B = t(A-B) — B. Similarly we can express a point on the second segment as parameter of s: s(C-D)-D.

Let's compute distance-squared between these points: sum[t(A-B) + s(C-D) + D — B]^2 [sum is over each of the coordinates] = sum[tE + sF + G]^2 (*).

To minimize this sum, we can partially differentiate with respect to t and s and hence we will get two equations: t(sum-of-E^2) + s(sum-of-EF) + (sum-of-GE) = 0 and t(sum-of-EF) + s(sum-of-F^2) + (sum-of-GF) = 0. Solving them we will get s and t.

And then we can plug value of s and t to (*) we will get the answer.

There is a corner case where the lines are parallel with the same direction vector. In such situation, we will have only one equation instead of 2. I plugged in s=0 to get a value for t, and the remaining part was same.

→ Reply

_LeMur_

6 years ago, # ^ |

← Rev. 2 →

+21

A: Find SALT with precalc. First find all numbers that satisfying second array (~4000 numbers). Then from that 4000 numbers find that number which satisfying first array.

→ Reply

6 years ago, # ^ |

How would you do this precalc? My simulation was too slow.

→ Reply

6 years ago, # ^ |

+15

Notice that you can go from the end (previous seed is determined uniquely)

→ Reply

6 years ago, # ^ |

Modulo was 2^31, so division is not unique right?

→ Reply

6 years ago, # ^ |

You multiply by odd number, so it is. All coprime numbers have unique inverse.

→ Reply

6 years ago, # ^ |

+10

So, is it like: [reference: 1 3 2 3 0 0 4 2] 1. loop over 0..2^31-1 and see if it's %5 = 2, 2. if so, find the previous seed, and check %5 = 4 ...

if all 8 passes, then this is a candidate.

So running over 2^31 numbers and doing something like 8 operations.

Is this your simulation? And it runs in reasonable time?

→ Reply

6 years ago, # ^ |

← Rev. 2 →

+10

Yes, but you continue after that to previous numbers (10k times go back for each number), It leaves only 1/5 of numbers each time so it works faster then is mod*8, it's like mod*5/4 or so, it's not so much especially considering you almost don't use memory

→ Reply

KAN

6 years ago, # ^ |

+20

I used two steps:

check only for the last 8 integers, skipping the long generation of 80000 integers: you can perform k steps of generator in O(log(k)) with matrix exponentiation or in O(1) with precalc if k is fixed.
If the last 8 integers match, I also check the first 8.

→ Reply

cdkrot

6 years ago, # ^ |

+10

Even better: we can bruteforce only "good seeds after 80k iterations skipped", and then only with the succeeding seeds perform 80k roll-backs and checking that power sequence is the same as we want.

→ Reply

6 years ago, # ^ |

A way to do it without reversing the random number generator is to use a circular buffer for the random values.

Start with some seed. Compute the first 80 008 pseudorandom values and put them in an array. Look if the last 8 values, pseudorandom numbers with indices 80 000-80 007 in the array, give the required Gene array if taken mod 5. It happens fairly rarely, like 2³¹ / 5⁸ times. If it did happen, use the previous 80 000 values to slowly check the Power array.

Now suppose it didn't work on the first try. Generate the next random value, and check for the numbers with indices 80 001-80 008, all mod 5, that they give the required Gene array. Then generate the next random value and check the numbers with indices 80 002-80 009, and so on.

Lastly, note that we should store only the last 80 008 pseudorandom numbers in this approach, so use a circular buffer to store them: for example, an array of size 131 072 which is accessed as Index mod 131072 every time we use it.

This approach takes 3-4 minutes to check all 2³¹ possible values of Salt (and probably finds the right one a bit faster, depending on where you started).

The Gene array is not necessary at first glance, but actually makes our task easier as shown above. But there is also a fast approach which does not use it. Same as above, start with some seed and generate 80 000 first pseudorandom numbers r_i. Calculate the sum of r₀ to r₉₉₉₉, the sum of r_10 000 to r_19 999, and so on until the sum of r_70 000 to r_79 999. If they are the eight sums we need, great! Otherwise, it's easy to obtain the next eight sums r₁ to r_10 000, ..., r_70 001 to r_80 000 from them: for each sum, just subtract the first element and add the next one. And so on: generate the next pseudorandom value, get the next sums in O(1) each, check the eight sums, proceed if they don't match.

→ Reply

6 years ago, # |

← Rev. 2 →

H: Since the maximum area could be 10^30, I coded it in Java (BigInteger) [not sure if there is __int128 in yandex, never used it before]. Barely made it pass in 1.8s after several TLEs. Any better solution?

My solution was: binary search on the coordinates one by one. Since coordinate value can be 1000, so at most 10*log(1000) ~ 100 call to a function which says true/false to the question, whether the area of the big box is same as union of other boxes (after cutting those boxes by the query box). The union of other boxes can be computed by Inclusion-Exclusion.

→ Reply

6 years ago, # ^ |

We used random modulo in C++ to compare volumes. Still had to optimize a bit

→ Reply

ifsmirnov

6 years ago, # ^ |

← Rev. 2 →

+18

There is no need in binary searching over all values for a coordinate. The answer always coincides with some of the b_i, it gives log 10 instead of log 1000 and works fast enough. I used __int128 and didn't have to do any extra optimizations.

→ Reply

tanphatls987

6 years ago, # ^ |

← Rev. 2 →

+20

After coordinate compression, the area is only 40¹⁰ so no need for BigInteger.

→ Reply

cdkrot

6 years ago, # ^ |

+10

__in128_t, c++, yandex. AC :)

→ Reply

awoo

6 years ago, # |

How to solve I?

→ Reply

Rezwan.Arefin01

6 years ago, # ^ |

+20

Give N distinct random odd numbers, so all of them has inverse.
Then take a number from the given N / 2 number, and multiply this with inverses of your numbers. So you have N candidates for X.
Now try other numbers from those N / 2 numbers and in each step you'll get another N candidates for X, but only keep the intersection of these candidates and previous candidates. Since the N / 2 numbers is random, the number of candidates will soon become 1.

→ Reply

TooDumbToWin

6 years ago, # |

← Rev. 2 →

How to solve E? I tried to write a solution using __int128, but it seems to be overflowing (not sure, got WA on test 12 and TLE in Pypy on same test). What are the bounds for the final result?

→ Reply

halyavin

6 years ago, # ^ |

← Rev. 2 →

+59

The limit is about 10⁴⁵-10⁴⁶ for numerator and 10³⁰-10³¹ for denominator. We used BigInteger in Java.

→ Reply

tanphatls987

6 years ago, # |

+36

How to solve C?

→ Reply

tunyash

6 years ago, # ^ |

+32

Let's consider some pair of vertices (u, v). Optimal path could be written as a sequence of vertices u = a₀, a₁, ..., a_p = v. Obviously the edge a₀ → a₁ belongs to some clique A and edge a₁ → a_p belongs to some clique B. The crucial observation is that if we fix the cliques A and B we are able to find the path between u and v without looking at the individual vertices but only at the cliques. Every edge in the path between u and v belongs to one or several cliques. Let's call a pair of cliques C₁ and C₂ connected if there exists vertex x belongs to both C₁ and C₂. The path between u and v could be decribed as a sequence of cliques A = A₁, A₂, ..., A_p - 1 = B where A_i connected with A_i + 1. It's obvious that with given vertices of the path we can easily find the indices of the cliques. On the other hand given the indices of the cliques we can by definition choose a common vertex for every consecutive pair of cliques and add the starting and the ending vertices.

Let's consider a graph G where each vertex corresponds to a clique and there is a directed edge i → j with the weight a_j (weight of clique number j) if i and j are connected. Then for every pair (u, v) such that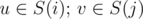 $\text{[math]}$ (S(k) is the set of vertices of clique k). dist(u, v) ≤ dist_G(i, j) + a_i where dist_G is the distance between the cliques i and j in G. dist_G could be found in O(k³) with Floyd-Warshall algorithm. G itself could be constructed by definition in O(n·k²).

Then all what we have to do is for every pair of cliques (i, j) find the number of vertices such that the optimal path for these pairs corresponds to the path between i and j in G. Let's process pairs of cliques in the increasing order of a_i + dist_G(i, j) and at each step find the number of pairs (u, v) such that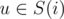 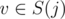$\text{[math]}$ ; $\text{[math]}$ and (u, v) was not considered at previous steps. Then if this number is denoted a x we should increase the answer by x·(a_i + dist_G(i, j)) because for these pairs there is no better path. Let's enumerate 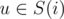$\text{[math]}$ . For every clique i we will maintain set of cliques D(i) such that 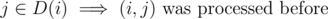$\text{[math]}$ . Denote cliques where u belongs as i₁, i₂, ..., i_p. Pair (u, v) should be counted at this step iff 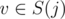$\text{[math]}$ and $\text{[math]}$ . 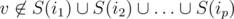Assuming that for every possible set of cliques {c₁, ..., c_p} we calculated α({c₁, ..., c_p}) the number of vertices w such that 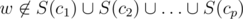$\text{[math]}$ the intended number of vertices u could be found as $\text{[math]}$ .

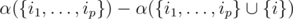So, only thing we should do is to calculate α for each of 2^k sets of cliques. First of all we can find β(I) the number of vertices belongs to cliques from set I and doesn't belong to any other cliques. Then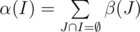 $\text{[math]}$ . Even if we calculate alpha in straightforward way enumerating all the subsets of 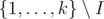$\text{[math]}$ one can proof that we will have time complexity O(3^k) and it was enough to get accepted.

But there is a way to calculate α in O(2^k·k). It's easier to calculate α'(I), the number of vertices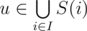 $\text{[math]}$ . Let's use dynamic programming: dp[mask][j] (where mask is the string of k zeroes and ones) is the number of vertices w such that for i < j 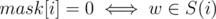$\text{[math]}$ and for i ≥ j 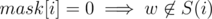$\text{[math]}$ . dp[mask][k] = β(mask). For j < k dp[mask][j] = dp[mask][j + 1] + x where x = 0 if mask[j] = 0 and x = dp[mask'][j] (where 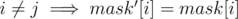$\text{[math]}$ and mask'[j] = 0) otherwise.

For every vertex denote M(v) as a string of zeroes and ones such that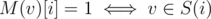 $\text{[math]}$ . Then first summand in dp corresponds to vertices with M(v)[j] = mask[j] and the second summand corresponds to vertices with M(v)[j] ≠ mask[j] (if mask[j] = 0 we should not calculate it). Finally it's pretty clear that α'(S) = dp[S][k].

This is it, now we have a solution with time complexity O(2^kk² + n).

→ Reply

6 years ago, # |

+18

How to solve J?

→ Reply

greencis

6 years ago, # |

+10

How to solve B and L?

→ Reply

tunyash

6 years ago, # ^ |

← Rev. 2 →

+28

B, very briefly. Let's delete all vertices such that one of the sinks is unreachable from them.

Notice that for every vertex x of a correct machine the set of edges on any path from the source to x contains the same set of edges. It follows from the fact that any path from the source to the 1-sink have to contain all the edges (can you see why?).
Moreover, for every vertex x of a correct machine and for every pair of paths from the source to x and for every vertex of G the parity of the sum of the values of the edges is the same on both paths. The argument is similar to (1).
One can verify (1) and (2) using hashing.
if (1) and (2) hold then f(x) = 1 implies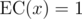 $\text{[math]}$ .
The only possibility for an error is x such that f(x) = 0 but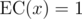 $\text{[math]}$ .
The case (5) happens if and only if there is a vertex of the machine x labeled with an edge e such that e is not a bridge in the graph G - e'₀ - e'₁ - ... - e'_k where e'₁, ..., e'_k are the edges on a path from the source to x.
(6) could be verified using disjoint set union with rollbacks.

→ Reply

pavel.savchenkov

6 years ago, # |

← Rev. 2 →

+47

Solution sketches for some problems:

While traversing through the machine we can watch for a state of the graph -- mask of size k there 1 is corresponding to not satisfied nodes. Initially this mask is equal to the array c. After going along an edge from v to u in the machine state may change -- if this edge was labeled with 1 then values of endpoints of the edge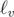 $\text{[math]}$ in the graph must be flipped. Our goal is to check if each path to t₁ corresponds to an empty mask and if each path to t₀ corresponds to a nonempty mask.

Let's note some facts about the case then answer is YES:

in each path from s to t₁ all m labels must be present, because otherwise we can freely change value of not presented edge and one of the corresponding states will be nonempty, but still leads to t₁
previous fact and the fact that in each path from s to t_i all labels are distinct mean that if one can reach t₁ from some node v then $\text{[math]}$ paths from s to v use the same set of edges in the graph
if one can reach t₁ from some node v then $\text{[math]}$ path from s to v must correspond to the same state of the graph, otherwise one can reach t₁ with 2 different masks

It is easy to check 1. and find corresponding counterexample if it exists. 2. and 3. can be checked with hashing the state of the graph: generate random z_v for each 1 ≤ v ≤ k, hash of the state will be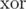 $\text{[math]}$ of all not satisfied nodes. It is easy to update this hash then values of 2 nodes in mask changes -- just 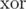$\text{[math]}$ it with $\text{[math]}$ .

Now we can assume that if some configuration of edges in the graph leads to t₁ then it is really 1. The last thing to check is existence of configuration of edges leads to t₀ but have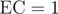 $\text{[math]}$ . Consider edge in the machine from v to u such that it is possible to get to t₁ from v, but not possible from u. Each path to v uses the same set of edges in the graph and corresponds to the same state of the vertices of the graph. From u we could only get to t₀, so the task here is to check whether we can assign some values to not used edges of the graph so that final state will be empty (all k zeros). We can do that iff in each connected component of not used edges xor sum of values of nodes in mask is zero. We can check that using dsu (disjoint set union) data structure with rollbacks: run dfs over back edges of the machine starting with t₁. Because in each path to t₁ all m edges were used then dfs reaches the node v it will contain exactly connected components of not used edges. To check if state is still ok after going along the edge from v to u it is enough to check if endpoints of 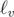$\text{[math]}$ are in the same connected component (in case of edge from v to u labeled with 1 of course).

If n = k then answer is YES.

Note the following facts:

if the answer is not prefix then it is must be nondecreasing
if the answer is not suffix then it is must be nonincreasing

If the answer if not prefix and not suffix than it is k consecutive maximums of the array. If the answer is suffix of length k than it is nondecreasing and a_{n - k + 1} must be not less than all a_i with 1 ≤ i < n - k + 1. The same for prefix. All these cases are easy to check in O(n).

Ask "?" Q times. Select 2 strings from the input, denote them by s' and t'. Let's think that they were generated from different base strings s and t. Cluster all the remaining string in 2 clusters based on distance to s' and t'. Construct S and T by selecting the most frequent digit in each position in corresponding cluster. Check if S and T could generate given Q input strings (each input string has distance exactly K to S or to T). If everything is OK, output S and T.

Let's provide some intuition about correctness of this solution.

What is the probability that some incorrect S and T pass the final check? It means that some 25 strings were generated from s, but some S ≠ s has distance K to each of them. But we can reconstruct s from these 25 strings: with probability ≈ 0.999983 some position was flipped <13 times, and with probability ≈ 0.998312 each position was flipped <13 times. This is a lower bound for the correct probability. In reality situation is even better since we construct S and T in a special way.

So we will win if for some pair of strings s' and t' from the input S and T appears to be equal to s and t respectively. If distance between s and t are big then each string almost certainly will be in correct cluster, if distance between s and t are small then actually small number of positions are unknown and correct configuration of these positions will be found fast.

To solve this problem one don't have to write down some probabilities, because it is very easy to verify correctness of solution locally.

Authors tried to find at least one test run there model solution fails, but didn't succeed.

4 variables fully define the entire table:
* number in the left upper corner;
* difference of adjacent elements in the first row;
* difference of adjacent elements in the second row;
* difference of adjacent elements in the first column;

So one can solve system of linear equations over these variables. Be careful with small tables and thin table.

We have to consider two separate cases: 1) there are two tangent planes, 2) there is only one tangent plane or no tangent planes.

The second case is easier, so we are going to describe only the first case. First of all, we need to understand the structure of the surface of the convex hull. It comprises the following parts: two equal triangles, which lie on two tangent planes; for each pair of spheres there is a part of the cone, tangent to these two spheres; for each sphere there is a part of the surface of this sphere.

It's convenient to start the solution by finding the normals to the tangent planes. If we can't find two distinct normals, then it's the second case and we do not discuss it here. Let O₁, O₂, O₃ be the centers of the spheres. Now, for convenience, we will suppose, that the plane that contains these three points is horizontal, and that the cross product (O₂ - O₁) × (O₃ - O₁) is in upwards direction.

Let A₁, A₂, A₃ be the touching points of the upper tangent plane and spheres and let B₁, B₂, B₃ be the touching points of the lower tangent plane. First, we calculate the volume of the polyhedron with the vertices O₁, O₂, O₃, A₁, A₂, A₃. The volume of the polyhedron with the vertices O₁, O₂, O₃, B₁, B₂, B₃ is the same. Next, we should calculate the volume of the parts of the cones. Consider, for instance, the cone between first and second spheres. Consider the three-dimensional shape with vertices O₁, A₁, A₂, O₂, B₂, B₁, with surface that consists of the part of the cone between first and second spheres, rectangles O₁, O₂, A₂, A₁ and O₁, O₂, B₂, B₁ and also two parts of cones with vertices O₁ and O₂. It's possible to write down the formula for the volume of such shape. We add to the answer this volume and analogous volumes of shapes between two other pairs of spheres.

Finally, it remains to calculate the volume of the parts of the balls. It's just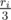 $\text{[math]}$ times the area of the part of the sphere. How does the part of the sphere looks like? It's bounded by two arcs of two circles, which are not geodesics. This problem is analogous to the following well-known problem: find the area of the union of two circles on plane. But in our case we should find the area of the union of two circles on sphere. This can be solved in a standard way.

For instance, consider the part of the first sphere. It's a union of two circles on the first sphere. These circles intersect in points A₁, B₁. Consider the geodesic between this two points. It separates our part of the first sphere in two parts. We calculate their areas separately. Each part is bounded by one geodesic between A₁ and B₁ and one arc of some circle between these two points. So, we need to calculate the volume of the segment of the circle on the sphere. To do this, we need to calculate the area of the sector of the circle and subtract the area of triangle.

→ Reply

6 years ago, # ^ |

← Rev. 2 →

In L, A few questions:

How to compute A's or B's?
"there is only one tangent plane or no tangent planes." -> How does the one tangent plane case look like? I can think of only two cases, one with two tangent planes, another with very small radius sphere inside a tunnel consisting of convex hull of other two spheres.
"It's possible to write down the formula for the volume of such shape. " -> How do you find the formula? Any easy trick or calculus? or may be there is some name of the shape and formula in internet/wikipedia?

→ Reply

ershov.stanislav

6 years ago, # ^ |

+10

First, we note that the vectors O_iA_i are collinear and normal to the tangent plane. So, all we need is to find this normal. Consider all planes that touch first and second spheres (but not necessarily the third). Consider normals to them. Their locus is a circle on the unit sphere. So we need to intersect this circle with the analogous circle for spheres 1 and 3.
Imagine a plane and a line on this plane. Now consider 3 spheres that touch both this plane and this line. Consider, for instance, the case when the middle sphere has radius greater than the radii of two other spheres. I think that in this case there is only one tangent plane. You shouldn't care about that in your solution, anyway.
It can be calculated using calculus, if we note that the shape is a solid of revolution.

→ Reply

ershov.stanislav

6 years ago, # ^ |

+10

You can check my solution here.

If you would like to look at the solution I used for stress-testing, here it is. This solution does the following: first, we consider a big cube, that contains our spheres. On each step we divide this cube into 8 parts, and remove those parts which lie outside or inside the convex hull. It's hard to check that the cube lies outside the convex hull, so instead of it I check that circumscribed sphere of the cube does not intersect the convex hull. After several steps we are left with some cubes which lie along the boundary. Finally, we can use Monte-Karlo method to calculate the volume of the intersection of these remaining cubes and the convex hull.

→ Reply

6 years ago, # ^ |

← Rev. 2 →

Seems that tests for J were weak. Seems that hardest tests against solutions I have seen were s=t=0 and s = neg(t).

→ Reply

pavel.savchenkov

6 years ago, # ^ |

You are right, many unexpected solutions passed. We had several solutions which calculated some statistics independently for positions and all of them failed in several tests, but some contestants used slightly different approaches/magic constants and got AC :(

→ Reply

6 years ago, # ^ |

You should just make more tests. Seems that 50 tests of both these types were enough

→ Reply

pavel.savchenkov

6 years ago, # ^ |

Yes, more tests is better. Also for some solutions tests with strings different in one position were special, for example.

→ Reply

6 years ago, # ^ |

Usually they also fail on all different. Basically you have problem with two equal letters which looks like different or with two different looks like the same.

→ Reply

Mano

6 years ago, # |

← Rev. 2 →

Can someone give statements of the problems please?

→ Reply

AryssonFigueiredo

6 years ago, # ^ |

You can download statements at upper-right corner, near "Jury messages" button.

→ Reply

coderbond007

6 years ago, # |

+27

Is it possible to add the Grand Prix contests to Codeforces Gym? I think there are many people here who want to solve problems of GPs, but are unable to solve due to Sector issue and many more.

→ Reply

Mano

6 years ago, # |

+10

How to solve D?

→ Reply

6 years ago, # ^ |

+15

Consider rotating the plane a bit:

The fat squares comprise a grid corresponding to the crosses. There are at least two ways from here:

For each square, find the center square of its cross, and then calculate the Manhattan distance between crosses.
Note that the centers of the smaller squares are in the corresponding cross if and only if they are in the corresponding fat square. So instead of finding the center of the cross, we can just do some rounding.

→ Reply

6 years ago, # ^ |

← Rev. 3 →

+10

It's probably will get down to the same formulas, but your interpretation seems beautiful but too hard to actually come up with.

What we did: Suppose we are going from cross center to cross center: Then we will make several(possibly negative number) (2, 1) moves and several (-1, 2) moves. Then just solve linear system of 2 variables and 2 equations. Now, to get cross center we just need to check initial cell and 4 its neighbours to check if they are in the form mentioned in the statement (again, 2x2 linear system. need to check whether answer is integral)

→ Reply

6 years ago, # ^ |

+10

Yeah, my solution, in code, is actually translating coordinates (x, y) into ((2x + y) / 5, (x - 2y) / 5), which is the same thing you will get after solving the system of linear equations.

And I think one way to achieve it is not actually harder than the other. Just that some people prefer visualization, and some other prefer formulas. From the people I've met, both "groups" (in my subjective classification) had individuals which had been very successful at mathematics and algorithms.

→ Reply

6 years ago, # ^ |

+10

We solved exactly as Gassa told. I don't think it was hard.

→ Reply

AryssonFigueiredo

6 years ago, # |

A: Shouldn't all pet powers be 500? Regardless of seed, Random() multiplies it by 1234567893 (multiple of 3) and adds 151515151 (equal 1 mod 3). Hence, Random() return value will always be 1 mod 3, and inside GenerateRandomPower(), Result value in each iteration will be the same (500). Am I missing anything?

→ Reply