Educational Codeforces Round 52 Editorial

#	User	Rating
1	tourist	3985
2	jiangly	3814
3	jqdai0815	3682
4	Benq	3529
5	orzdevinwang	3526
6	ksun48	3517
7	Radewoosh	3410
8	hos.lyric	3399
9	ecnerwala	3392
9	Um_nik	3392

#	User	Contrib.
1	cry	169
2	maomao90	162
2	Um_nik	162
4	atcoder_official	161
5	djm03178	158
6	-is-this-fft-	157
7	adamant	155
8	awoo	154
8	Dominater069	154
10	luogu_official	150

Tutorial

Solution (Ajosteen)

#include <bits/stdc++.h>

using namespace std;

int main() {
    int s, a, b, c;
    int t;
    cin >> t;
    for(int i = 0; i < t; ++i){
        cin >> s >> a >> b >> c;
        
        s /= c;
        int x = s / a;
        s %= a;
        long long res = x * 1LL * (a + b);
        res += s;
        
        cout << res << endl;
    }
    return 0;
}

1065B - Vasya and Isolated Vertices

Tutorial

Solution (Ajosteen)

#include <bits/stdc++.h>

using namespace std;

int main() {
    int n;
    long long m;
    cin >> n >> m;
    long long cur = 1;
    long long rem = m;
    while(rem > 0){
        long long d = min(cur, rem);
        rem -= d;
        ++cur;
    }
    assert(rem == 0);
    
    long long res = n;
    if(cur > 1) res = n - cur;
    
    cout << max(0ll, n - m * 2) << ' ' << res << endl;
    return 0;
}

1065C - Make It Equal

Tutorial

Solution (Ajosteen)

#include <bits/stdc++.h>

using namespace std;

const int N = int(2e5) + 9;

int n, k, h;
int need = int(1e9);
int cnt[N];

int main() {
    scanf("%d %d", &n, &k);
    for(int i = 0; i < n; ++i){
        int x;
        scanf("%d", &x);
        h = max(h, x);
        need = min(need, x);
        ++cnt[x];
    }
    
    int pos = N - 1;
    int res = 0;
    long long sum = 0;
    int c = 0;
    while(true){
        long long x = sum - c * 1LL * (pos - 1);
        if(x > k){
            ++res;
            h = pos;
            sum = pos * 1LL * c;
        }   
    
        --pos;
        if(pos == need) break;
        c += cnt[pos];
        sum += cnt[pos] * 1LL * pos;
    }
    
    if(h != need) ++res;
    
    cout << res << endl;
}

1065D - Three Pieces

Tutorial

Solution (PikMike)

#include <bits/stdc++.h>

#define forn(i, n) for (int i = 0; i < int(n); i++)
#define mp make_pair
#define x first
#define y second

using namespace std;

typedef pair<int, int> pt;

const int N = 12;
const int M = 305;
const int INF = 1e9;

int n;
int a[N][N];
pt pos[N * N];
pt dist[M][M];

pt operator +(const pt &a, const pt &b){
    return mp(a.x + b.x, a.y + b.y);
}

int dx[] = {-2, -1, 1, 2,  2,  1, -1, -2};
int dy[] = { 1,  2, 2, 1, -1, -2, -2, -1};

bool in(int x, int y){
    return (0 <= x && x < n && 0 <= y && y < n);
}

int get(int x, int y, int p){
    return x * n * 3 + y * 3 + p;
}

pt dp[N * N][3];

int main() {
    scanf("%d", &n);
    forn(i, n) forn(j, n){
        scanf("%d", &a[i][j]);
        --a[i][j];
        pos[a[i][j]] = mp(i, j);
    }
    
    forn(i, M) forn(j, M) dist[i][j] = mp(INF, INF);
    forn(i, M) dist[i][i] = mp(0, 0);
    
    forn(x, n) forn(y, n){
        forn(i, 8){
            int nx = x + dx[i];
            int ny = y + dy[i];
            if (in(nx, ny))
                dist[get(x, y, 0)][get(nx, ny, 0)] = mp(1, 0);
        }
        
        for (int i = -n + 1; i <= n - 1; ++i){
            int nx = x + i;
            int ny = y + i;
            if (in(nx, ny))
                dist[get(x, y, 1)][get(nx, ny, 1)] = mp(1, 0);
            ny = y - i;
            if (in(nx, ny))
                dist[get(x, y, 1)][get(nx, ny, 1)] = mp(1, 0);
        }
        
        forn(i, n){
            int nx = x;
            int ny = i;
            dist[get(x, y, 2)][get(nx, ny, 2)] = mp(1, 0);
            nx = i;
            ny = y;
            dist[get(x, y, 2)][get(nx, ny, 2)] = mp(1, 0);
        }
        
        forn(i, 3) forn(j, 3){
            if (i != j){
                dist[get(x, y, i)][get(x, y, j)] = mp(1, 1);
            }
        }
    }
    
    forn(k, M) forn(i, M) forn(j, M)
        dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
    
    forn(i, N * N) forn(j, 3) dp[i][j] = mp(INF, INF);
    dp[0][0] = dp[0][1] = dp[0][2] = mp(0, 0);
    forn(i, n * n - 1) forn(j, 3) forn(k, 3)
        dp[i + 1][k] = min(dp[i + 1][k], dp[i][j] + dist[get(pos[i].x, pos[i].y, j)][get(pos[i + 1].x, pos[i + 1].y, k)]);
    
    pt ans = mp(INF, INF);
    ans = min(ans, dp[n * n - 1][0]);
    ans = min(ans, dp[n * n - 1][1]);
    ans = min(ans, dp[n * n - 1][2]);
    
    printf("%d %d\n", ans.x, ans.y);
    return 0;
}

1065E - Side Transmutations

Tutorial

Solution (PikMike)

#include <bits/stdc++.h>

#define forn(i, n) for (int i = 0; i < int(n); i++)

using namespace std;

const int N = 200 * 1000 + 13;
const int MOD = 998244353;

int n, m, A;
int b[N];

int add(int a, int b){
    a += b;
    if (a >= MOD)
        a -= MOD;
    return a;
}

int mul(int a, int b){
    return (a * 1ll * b) % MOD;
}

int binpow(int a, int b){
    int res = 1;
    while (b){
        if (b & 1)
            res = mul(res, a);
        a = mul(a, a);
        b >>= 1;
    }
    return res;
}

int cnt(int x){
    int base = binpow(A, x);
    return mul(add(mul(base, base), base), (MOD + 1) / 2);
}

int main() {
    scanf("%d%d%d", &n, &m, &A);
    forn(i, m)
        scanf("%d", &b[i]);
    
    int ans = binpow(A, n - b[m - 1] * 2);
    ans = mul(ans, cnt(b[0]));
    forn(i, m - 1)
        ans = mul(ans, cnt(b[i + 1] - b[i]));
    
    printf("%d\n", ans);
    return 0;
}

1065F - Up and Down the Tree

Tutorial

Solution (adedalic)

#include<bits/stdc++.h>

using namespace std;

#define fore(i, l, r) for(int i = int(l); i < int(r); i++)
#define sz(a) int((a).size())

#define x first
#define y second

typedef long long li;
typedef pair<int, int> pt;

template<class A, class B> ostream& operator <<(ostream& out, const pair<A, B> &p) {
    return out << "(" << p.x << ", " << p.y << ")";
}

template<class A> ostream& operator <<(ostream& out, const vector<A> &v) {
    out << "[";
    fore(i, 0, v.size()) {
        if(i) out << ", ";
        out << v[i];
    }
    return out << "]";
}

const int INF = int(1e9);
const li INF64 = li(1e18);

const int N = 1000 * 1000 + 555;

int n, k;
vector<int> g[N];

inline bool read() {
    if(!(cin >> n >> k))
        return false;
    fore(i, 1, n) {
        int p; assert(scanf("%d", &p) == 1);
        p--;
        
        g[p].push_back(i);
        g[i].push_back(p);
    }
    return true;
}

int h[N];
pt drev[N];

void calcRev(int v, int p) {
    drev[v] = pt(INF, 0);
    for(int to : g[v]) {
        if(to == p) continue;
        
        h[to] = h[v] + 1;
        calcRev(to, v);
        
        if(drev[to].x <= h[v]) {
            drev[v].x = min(drev[v].x, drev[to].x);
            drev[v].y += drev[to].y;
        }
    }
    
    if(p >= 0 && g[v].size() == 1)
        drev[v] = pt(h[v] - k, 1);
}

int d[N];

void calcAns(int v, int p) {
    d[v] = (p >= 0 && g[v].size() == 1);
    for(int to : g[v]) {
        if(to == p) continue;
        calcAns(to, v);
        
        int tmp = drev[v].y;
        if(drev[to].x <= h[v])
            tmp -= drev[to].y;
        
        d[v] = max(d[v], tmp + d[to]);
    }
}

inline void solve() {
    h[0] = 0;
    calcRev(0, -1);
    calcAns(0, -1);
    cout << d[0] << endl;
}

int main() {
#ifdef _DEBUG
    freopen("input.txt", "r", stdin);
    int tt = clock();
#endif
    cout << fixed << setprecision(15);
    
    if(read()) {
        solve();
        
#ifdef _DEBUG
        cerr << "TIME = " << clock() - tt << endl;
        tt = clock();
#endif
    }
    return 0;
}

1065G - Fibonacci Suffix

Tutorial

Solution (BledDest)

#include <bits/stdc++.h>

using namespace std;

typedef long long li;

const li INF64 = li(1e18);

li add(li x, li y)
{
    return min(x + y, INF64);
}

const int N = 243;

int A1[N][2];
li A2[N][N];
int A3[N][N];
int n, m;
li k;
int z;
int p[N];

void build(const string& s)
{
    z = (int)(s.size());
    p[0] = 0;
    for(int i = 1; i < z; i++)
    {
        int j = p[i - 1];
        while(j > 0 && s[j] != s[i])
            j = p[j - 1];
        if(s[j] == s[i])
            j++;
        p[i] = j;
    }
    for(int i = 0; i <= z; i++)
        for(int j = 0; j < 2; j++)
        {
            if(i < z && s[i] == char('0' + j))
                A1[i][j] = i + 1;
            else if(i == 0)
                A1[i][j] = 0;
            else
                A1[i][j] = A1[p[i - 1]][j];
        }
    for(int i = 0; i <= z; i++)
        for(int j = 0; j < 2; j++)
        {
            A3[i][j] = A1[i][j];
            A2[i][j] = (A3[i][j] == z ? 1 : 0);
        }
    for(int i = 2; i <= n; i++)
        for(int j = 0; j <= z; j++)
        {
            A3[j][i] = A3[A3[j][i - 2]][i - 1];
            A2[j][i] = add(A2[j][i - 2], A2[A3[j][i - 2]][i - 1]);
        }
}

int main()
{
    cin >> n >> k >> m;
    string cur = "";
    for(int i = 0; i < m; i++)
    {
        if(cur != "") build(cur);
        li x = 0;
        if(cur != "" && A3[0][n] == i)
            x = 1;
        if(k == 1 && x == 1)
            break;
        k -= x;
        build(cur + '0');
        li x1 = A2[0][n];
        if(k > x1)
        {
            cur += '1';
            k -= x1;
        }
        else
            cur += '0';
    }
    cout << cur << endl;
    return 0;
}

Comments (26)

Show archived | Write comment?

BRCode

6 years ago, # |

44220948

Why does my D WA on test 25? I had a similar solution, except I bruteforced the shortestdistance instead of using bds/djikstras, and used a bunch of selections for the dp instead of a pair.

→ Reply

MZuenni

6 years ago, # ^ |

← Rev. 2 →

+11

You probably didnt consider that in the optimal solution you need to change the chess piece on the way between position a and b and not only change pieces on position a or b?

-6

but a rook can always reach your desired position in 2 moves, so even if you switch to a rook at the beginning your total cost will be 3

Now if you're using a bishop and move to a position which isn't your destination, and switch to another counter and then move to your desired position, your total cost would still be 3

The same goes for switching between other counters. Your maximum cost will always be 3 (which is the same as switching to a rook at the beginning and then reaching your desired position)

LmnGz

Consider, when you are in number 2 with a bishop.

You can go to number 3 with a rook in 3 steps: replace bishop with rook, goto 14, goto number 3.
You can go to number 3 with a knight in 3 steps: go back to 1 with bishop, replace bishop with knight, goto number 3. (Note that, you cannot replace bishop with knight in number 2 because, in that case, you need 4 steps to go to number 3)

Xylenox

Well, what if you number the positions as the positions of a knights tour? Then the optimal solution would be to start with a knight and the distance between each location would be 1.

tfg

+16

O((N + M) * M) or O(M * (M + log(N))) solution for G:

Same solution but changing 1 part, the part of counting the number of occurences. Instead of using an automaton, keep pref[i] ans suf[i] as the M first characters of the prefix/suffix of the i-th string. Using this, freq[i] = freq[i-2] + freq[i-1] + occurences that use the suf[i-2] + pref[i-1]. This gives us an O(N * M^2) solution like in the editorial. But you can note that starting from one point (the position where |F[i]| >= M), pref[i] == pref[i + 2] and suf[i] == suf[i + 1]. This means that the "occurences that use the suf[i-2] + pref[i-1]" will actually repeat with period 2. So you can calculate it in one phase until that point, the cost of this is O(F[0] + F[1] + F[2] + ... + F[i]) = O(F[i + 1]) = O(M) and from that point on, you can reuse the number of occurences that happened in the previous calculations (or do 4 more just to be safe and use from that point on, doesn't change the complexity). Total complexity: O((N * M) * M) with one phase (additional character) happening in O(M + N) because you need to calculate the borders for KMP. You can actually use this fact to create a linear recurrence relation for freq[i] and use matrix exponentiation (the column matrix keeps freq[i], freq[i-1], the transitions and keep swapping them) starting from the point that it repeats, this would result in a O(log(M) + M + log(N) * 4^3) phase per character in the answer. The log(M) comes from the fact that fib is exponential, so the point that it starts repeating is O(log(M)). This would result in a O(M * (M + log(N))) solution.

Code for O((N + M) * M) solution: http://mirror.codeforces.com/contest/1065/submission/44225229

Edit: If there's an occurence in the transition, you can also keep calculating until it breaks K. It will break K in O(logK) steps and if there's no occurence, you just break. So I guess the second part wouldn't be necessary for the O(M^2) complexity.

That also implies that a big N doesn't matter as can be seen here: http://mirror.codeforces.com/contest/1065/submission/44226008. n = min(n, 100) works. To be more exact, the bound on N mattering would be O(log(M) + log(K)).

Pj18

https://mirror.codeforces.com/contest/1065/submission/44147964

For C,my approach is a bit similar can anyone help me,where i am wrong?

zaidjan1295

Can someone explain d.

Kerpoo

Hi! I have a problem can anybody help? if u submit this solution for problem D with MS C++ u get accept! Link to code! but gnu++ gives WA! do u know why?

YuanyuanWu

Can E solve by polya?

BlackTools

Yes, you can. 44419650

As the editorial said every subset of segments [0..l₁), [l₁, l₂), …, [l_m−1, l_m) is achievable. There is a bijective relation between the set of subsets of segments and the set of transformations G and every transformation add A^n - k where k is the sum of the cardinalities of the segments in the associated subset.

Yes! Actually, the formula solve by polya is the same as the official tuitual. Wonderful!

mexikansky_voin

what is polya?

This may help you https://en.wikipedia.org/wiki/P%C3%B3lya_enumeration_theorem

chamanag

In the tutorial of Problem E: cnt function : why is there *(mod+1)/2 instead of /2 directly in the return. I am getting wrong answer with /2 but I am not able to understand why.

Suraj_IOI

Why this this solution for problem 1065C is not correct ?

Since the attainable equal height is the Smallest number.

then Number of Chops can be : ceil((SumOfHeight - N * minHeight) / K)

aryan29

Because we cant remove blocks parially from any particular height

mrsac7

3 years ago, # ^ |

aryan29's explanation is correct. Here, I'm providing a visual representation of a counter case so that people can get an intuitive understanding of the situation. Consider the test case:

3 3
5 3 1

Here ceil((SumOfHeight - N * minHeight) / K) will give 2 slices which is incorrect as we can not remove blocks from a height partially.

Whereas the correct number of slices is 3.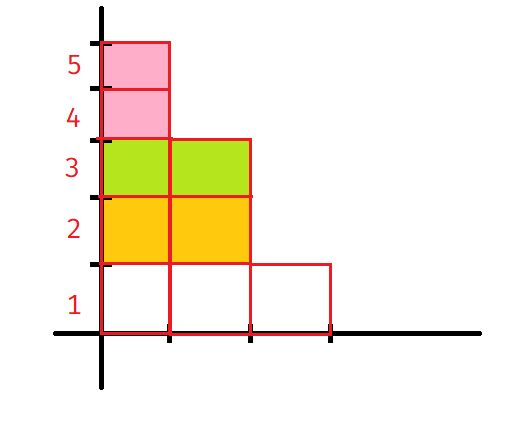

Yahia_NT

5 months ago, # ^ |

please why my does my C WA on test 9? https://mirror.codeforces.com/problemset/submission/1065/271734995 i store in h[i] the number of squares that are greater than or equal to i .

Robbinb1993

Problem D can be solved with a single BFS using a state of four dimensions: current x, current y, piece type, current square we are at. The result is the minimum among final states. https://mirror.codeforces.com/contest/1065/submission/46351519

Blurryface

4 years ago, # |

Can anyone explain 1065C?I didn't understand the editorial.thanks in advance.

ashish_kumarsoni

4 years ago, # ^ |

here is my code that may help u. if u don't understand then sorry. https://mirror.codeforces.com/contest/1065/submission/91731954

towrist

-8

Problem E is so nice. A subtle change in perspective, by viewing the string as a whole, solves it instantly!

rohit_goyal

Another solution for F : Let's convert this graph to SCC's and bridges, where each SCC component has a weight denoting number of distinct leaf nodes in that SCC. Start a dfs from the root, and when we hit each bottom, start uniting (union — find algorithm) the nodes on the basis of minimum distance of a leaf to their parents. Maintaining the weight of component is simple, initialize the weights of leaf components initially as 1, and non leaves as 0, take care of uniting weights while uniting nodes. Now we have a set of SCC's and to add bridges in between them, consider each edge in original tree not joining 2 nodes of same components. Now that we have a graph of SCC's and bridges, we need to find a path from root(component having node 1) to a leaf component having maximum sum of weights (maximum number of distinct leaves essentially). This is a simple dfs traversal, visit each child of a node, get maximum answer for respective children, and answer for parent is the weight of root + maximum of answers of all children. Time Complexity is O(N) or O(NlogN) depending on the implementation.

Note : You could do union of the complete graph in O(N) too.

5 months ago, # |

awoo's blog