alwerty's blog

Problem from Bloomberg Codecon qualifier
By alwerty, history, 6 years ago, In English

I tried all day to solve this problem:

Bring an integer N to 1 doing one of these operations each step: N /= 3; N /= 2; N -= 1;

1 <= N <= 1e9

output = minimum number of steps.

This is the function I wrote:


int solve(int n) {
    if (n == 1) return 0;
    if (n == 2) return 1;
    if (n % 3 == 0) {
        if (n % 2 == 0) return solve(n / 3) + 1;
        else return  min(solve(n / 3), solve((n - 1) / 2) + 1) + 1;
    }
    if (n % 2 == 0) {
        if ((n - 1) % 3 == 0) return min(solve((n - 1) / 3) + 1, solve(n / 2)) + 1;
        else return min(solve((n - 2) / 3) + 2, solve(n / 2)) + 1;
    }
    if ((n - 1) % 3 == 0) return min(solve((n - 1) / 3), solve((n - 1) / 2)) + 2;
    return min(solve((n - 2) / 3) + 1, solve((n - 1) / 2)) + 2 ;
}

I think the complexity of my solution is linear and the answer it gives should be correct but I'm not sure.

Can you help me find the best solution?

  • Vote: I like it
  • +3
  • Vote: I do not like it

»
6 years ago, # |
  Vote: I like it +19 Vote: I do not like it

Let's find answer for all n <= 10 ^ 7 = M, it can be done with simple dp. Then how to solve it for n > M? As we know ans[n] = min(ans[n / 2], ans[n / 3], ans[n — 1]) Well, let's run recursion, if n <= M: return dp[n]; else: we use our formula

But is still does not work fast, because we will find answer for n, n — 1, n — 2, ... M + 1. Notice that there is no point in decreasing n by 1 3 or more times because instead n -> n — 1 -> n — 2 -> (n — 2) / 2 we do n -> n / 2 -> n / 2 — 1, case when we divide n by 3 after several decreasing by 1 is the similar

Now let's run our recursion again, but in recursion we will check that we don't substract 1 3 or more times. And this solution should works fast

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    Yes this is a lot faster than without dp, can you explain briefly the dp algorithm done in linear time?

    EDIT: Nvm I think I got it, it is really simple indeed

    → Reply
»
6 years ago, # |
← Rev. 3   Vote: I like it +8 Vote: I do not like it

If we let R(N) be the answer for N, then:

The time complexity recurrence is $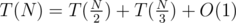 and this should be fast enough even without memoization. We can analyze it with the Akra-Bazzi method to find that the actual complexity is O(N0.79).

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    This is exactly what I did, but I realized it after I coded that mess.

    → Reply