Hello,
I found this Div 2 — A problem quite interesting. The tutorial gives a quadratic solution; however, I was wondering if there was a linear solution. Any ideas? Just for the fun.
Thanks.
| # | User | Rating |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
| # | User | Contrib. |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 161 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | Dominater069 | 154 |
| 8 | awoo | 154 |
| 10 | luogu_official | 150 |
Hello,
I found this Div 2 — A problem quite interesting. The tutorial gives a quadratic solution; however, I was wondering if there was a linear solution. Any ideas? Just for the fun.
Thanks.
| Name |
|---|



O(N*log(maxAi)) is well known .. See this problem. I don't know whether there is a linear solution, but in general case O(N*log(maxAi)) will almost always enough.
It is linear solution, as the size of input is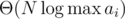 itself, so the time complexity of this solution grows linearly with input length.
itself, so the time complexity of this solution grows linearly with input length.
I think that CherryTree means O(N*log(maxAi)) integer operations, and this grows as log(max(Ai)) * input
It's a tricky question. We are often assuming O(1) operations with arbitrary-precision integers, but still consider them in time/space complexity. Which, I think, causes some strange situations. I'm not qualified in computational complexity theory, though I prefer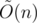 notation in such cases. :) Anyway, we are already too far from the subject.
notation in such cases. :) Anyway, we are already too far from the subject.
Actually, this is a problem like that: given two arbitary integers in decimal, compute xor of them. Suddenly, you're to convert them into binary, so... Let us denote input is O(1), xor is O(1) and ignore "арифметическую поправку асимптотических обозначений" (I don't know how it is called in English) :)
I think that there is a trick that allows you to have impractical, but better solution with following idea.
First of all, compute prefix xors and split them into parts with max_bit set and not set. (This is O(N))
This is the following problem now: given A and B, find i,j: a[i] ^ b[j] is maximal.
Split each array by k maximal bits (i.e. O(2^k) groups). Solve this problem for numbers of groups in O(k*2^k). Each group from A will be optimal with not more than one group from B. Let T(N,b) will be complexity of the solution. We have T(N,b) = sum (T(n[i], b-k)) + k*2^k + N, where sum of all n[i] is N. We can denote k like min(b, log(N/log(N))), and, I think, got T(N,b) like N*b/min(b, log(N/log(N)) as a result (possible, with some additional tricks).
So how to solve this problem in your link?
There is a link to the editorial in the problem.