GodSpeed98's blog

Need help in an interesting Graph Problem.
By GodSpeed98, history, 6 years ago, In English

I am stuck on this problem. https://www.codechef.com/problems/IOPC16K

Problem Statement:

Find out what will be the new shortest path if one of the edge on the original shortest path is removed.Find for all of the edges in shortest path path(Given Unique original shortest path).

Constraints:

no. of edges <= 1e5

no. of nodes <= 1e5

weights of edges <= 1e9

I Looked at some of the AC solutions but could not get the Idea. So if somebody can share the Idea to solve the problem it would be very Helpful! (I think its on some Algorithmic Paper).

  • Vote: I like it
  • +39
  • Vote: I do not like it

»
6 years ago, # |
← Rev. 2   Vote: I like it +5 Vote: I do not like it

alecsyde, being the setter for the problem, it would be great if you can share the solution for the problem or link to any other similar problem.

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it +5 Vote: I do not like it

Make the shortest distance tree rooted at s, and compute shortest distances from s and t. Let Ti be the subtree rooted at i. Let Ei be the set of the graph edges which connect Ti to V - Ti except the edge connecting i to its parent.

Now, for some ancestor i ≠ s of t, say edge (i, j) is removed such that j is the parent of i in the tree. Consider edges of form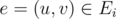 , such that 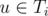. It can be proved that the deletion of edge (i, j) doesn't change the length of the shortest paths from s to v and from t to u (Try to prove it, its not that trivial). Thus, the new shortest path is minimum of d(s, v) + d(t, u) + wu, v over all such edges.

To compute efficiently for all edges in the shortest path, start from i = t move up to reach s in the tree and think about how the set E changes. You'll have to make a linear number of changes in the set overall (each edge would be inserted atmax once and deleted atmax once). Overall complexity is .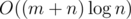

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it +5 Vote: I do not like it

    Ok. I got The Idea. Just to be Sure, I am restating your idea in my terms.

    1. The Distance Tree is formed as Prim MST is Computed.
    2. The Second theorem of not changing the Distance of S to u and then v to T is proved similar to meet in the middle approach of Dijkstra (I think i read it in CLRS though not sure).
    3. The edges is inserted in the set when the edge falls in the Cut of the tree. So insert once when one end falls in the subtree and then remove the edge if both falls in the subtree( case of Back edge or the Cross edge of same subtree).

    Thank you for the help and a prompt reply.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 2   Vote: I like it +5 Vote: I do not like it
      1. It is the tree formed when computing shortest distances with the property that any path from root is a shortest path.
      2. s to v is trivial (since the tree path from s to v is present even after deleting (i, j) and is also the shortest path ). For t to u consider any t - u path containing (i, j). Prove that the tree path from t to u (which we know doesn't contain (i, j)) is not longer than this path. I am not sure about how it is related to the meet in the middle approach.
      → Reply