Всем привет. Столкнулся с задачей :
Дан массив чисел длины n, 1 <= a[i] <= n, поступают запросы двух видов.
1) l r X Y ( 1 ≤ l ≤ r ≤ n , 1 ≤ X , Y ≤ n ) всем i, l <= i <= r, если arr[i] == X, то установить в arr[i] значение Y.
2) l r найти K-й порядковый элемент на отрезке с l по r.
n <= 10^5.
Хотел решить сам, но никак не выходит. Уже несколько дней не могу нормально спать)), помогите с решением, пожалуйста. Заранее спасибо.
→ Обратите внимание
→ Лидеры (рейтинг)
| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 3985 |
| 2 | jiangly | 3814 |
| 3 | jqdai0815 | 3682 |
| 4 | Benq | 3529 |
| 5 | orzdevinwang | 3526 |
| 6 | ksun48 | 3517 |
| 7 | Radewoosh | 3410 |
| 8 | hos.lyric | 3399 |
| 9 | ecnerwala | 3392 |
| 9 | Um_nik | 3392 |
| Страны | Города | Организации | Всё → |
→ Лидеры (вклад)
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 169 |
| 2 | maomao90 | 162 |
| 2 | Um_nik | 162 |
| 4 | atcoder_official | 160 |
| 5 | djm03178 | 158 |
| 6 | -is-this-fft- | 157 |
| 7 | adamant | 155 |
| 8 | Dominater069 | 154 |
| 8 | awoo | 154 |
| 10 | luogu_official | 151 |
→ Найти пользователя
→ Прямой эфир
↑
↓
Codeforces (c) Copyright 2010-2024 Михаил Мирзаянов
Соревнования по программированию 2.0
Время на сервере: 23.12.2024 10:25:07 (f1).
Десктопная версия, переключиться на мобильную.
При поддержке
Списки пользователей


| Название |
|---|











"Уже несколько дней не могу нормально спать))" — Плохо)
Ок, попробую написать решение, которое скорее всего должно пройти по времени:
Решение с использованием SQRT-декомпозиции по блокам
Естественно, можно хранить только один Фенвик Sum[i](сколько чисел меньше либо равно i) для всего блока, но тогда прыжки по памяти будут больше(зависит от тестов и компилятора!).
"Естественно, можно хранить только один Фенвик Sum[i](сколько чисел меньше либо равно i) для всего блока"
правильно ли я понял, что можно для каждого блока хранить дерево Фенвика длины n? Тогда как отвечать на запросы внутри одного блока?
Для каждого блока, помимо Фенвика/корневой нужно держать ещё массив next[block][i](*first, *last) (это пара, указатель на первый элемент в блоке который равен i и последний элемент в блоке, который равен i(порядок не важен), либо {NULL, NULL}, если нет чисел равных i).
Теперь, когда нужно сделать операцию X -> Y, смотрим если next[Block][X] не пустой, то коннектим их в один список: next[Block][X]->last -> next[Block][Y]->first, next[Block][Y]->first = next[Block][X]->first, next[Block][X]->first = next[Block][X]->second = NULL: O(1)
Для восстановления блока просто пробежим по всем возможным значениям (не более sqrt(N)) и проитерируемся по спискам элементов в них (мы знаем указатели на них) те значения, суммарно O(sqrt(N))
С учётом первой идеи ниже можно достичь решения со сложностью O(N sqrt(N))
Пусть над блоком были операции:
Тогда все элементы равные 1 должны быть равны 2, а элементы равные 3 должны быть равны 4, у тебя же будет записано next[block][1] = 4, next[block][3] = 1, что неверно.
На самом деле, в этой задаче не заходит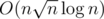 и нужно думать о более быстром решении.
и нужно думать о более быстром решении.
Решим задачу, если мы магическим образом умеем понимать какое число стоит на позиции i после применения всех запросов.
Давайте на каждом префиксе кратном насчитаем количество каждого числа (мы на это потратим
насчитаем количество каждого числа (мы на это потратим 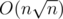 времени и памяти). Теперь в каждом таком префиксе все числа разобьем на блоки по корню и будем в каждом блоке помнить сумму.
времени и памяти). Теперь в каждом таком префиксе все числа разобьем на блоки по корню и будем в каждом блоке помнить сумму.
Тогда отвечать на запрос просто — нам надо взять разность двух префиксов и учесть эелементы с краев, поскольку у нас числа разбиты на блоки по корню, мы за корень находим нужный блок, а затем в нужном блоке ещё раз за корень находим нужное число, учёт элементов с краев тоже за корень.
Такие махинации с «корневой в корневой» были сделаны ради быстрого изменения, ибо теперь мы каждый блок обновляем за O(1), а, следовательно, изменение основной структуры у нас тоже за корень.
Единственная проблема — восстановление реальных чисел в конкретных позициях для случаев, когда концы запроса не кратны корню. Для этого разобъем массив на блоки по корню и будем в каждом хранить DSU. К сожалению в DSU нельзя просто так делать merge компонент и хранить реальное значение в компоненте. В качестве контртеста можно предъявить тест из начала комментария. Чтобы избежать этой проблемы, будем хранить dsu размера 2·n. А так же для каждого числа будем хранить, встречается ли оно хоть раз в блоке.
Когда нам пришёл запрос о переводе отсутствующего на отрезке числа, пропускаем этот запрос, иначе смотрим, если ли на отрезке число, в которое мы переводим. Если есть, просто делаем merge, иначе создаём «новую вершину» (с номером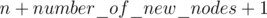 ), запоминаем что эта вершина отвечает за число Y, и делаем merge. Не забываем в каждой компоненте хранить реальное значение всех чисел из нее.
), запоминаем что эта вершина отвечает за число Y, и делаем merge. Не забываем в каждой компоненте хранить реальное значение всех чисел из нее.
Итоговая асимптотика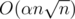
Спасибо за решение!
Да, восстановление чисел не так тривально.
Почему merge в dsu не за O(log)? Мы же соединяем деревья не меньшее к большему, а так как велят запросы
Никто не мешает делать merge меньшего к большему, просто после merge надо не забыть сделать что-то вида:
Это гениально!///. Но смогу ли я уместить все это в 512 МБ?
Размер блока не обязательно делать ровно , можно его немного двигать, чтобы влезло по памяти.
, можно его немного двигать, чтобы влезло по памяти.
Например можно выбрать 512, тогда еще операции деления будут соптимизированы битовыми сдвигами.
Также, немного усложнив код, можно сделать массивы для DSU размера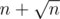 , а не
, а не  .
.
Теперь по памяти, каждый массив будет иметь размер примерно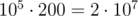 .
.
В итоге в коде тебе нужно всего 5 массивов такого размера (на каждый префикс, предки в DSU, ранги в DSU, real_value, where_value), это всего 108 4 байтных чисел (а вообще ранги можно хранить в char, так что еще меньше), что будет занимать примерно 382 МБ.
Если ты говоришь про эту задачу, то c блоком размера 512 там заходит за секунду примерно.
Огромное спасибо, структура DSU двойного размера просто нечто!!
deleted
ch_egor А можете пересдать на информатиксе эту задачу? Там сервер обновили, он стал в 2.5 раза медленнее (по крайней мере ejudge-vm-64). Предположительно, Ваше решение теперь не уложится в TL, но могу ошибаться
Можно сделать за O(log^2n) на запрос. Создадим дерево отрезков, а в каждой его вершине — декартово дерево. Будем поддерживать в ДД пару (число, кол-во). Тогда для обработки 1 запроса достаточно спуститься в нужную вершину ДО (которая соответствует отрезку [l;r]), в текущем ДД удалить число X и вставить пару (Y, кол-во удаленных X) (либо если существует, просто добавить это кол-во). Ну я думаю запрос 2 типа тривиален.
"Ну я думаю запрос 2 типа тривиален." отрезков
отрезков 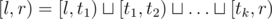 (это дерево отрезков), на каждом отрезке ты умеешь считать порядковую статистику за
(это дерево отрезков), на каждом отрезке ты умеешь считать порядковую статистику за  . Как тебе это поможет посчитать порядковую статистику на отрезке [l, r) за
. Как тебе это поможет посчитать порядковую статистику на отрезке [l, r) за 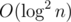 — непонятно, скорее всего никак. Может, можно получить
— непонятно, скорее всего никак. Может, можно получить 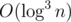 (но это будет оооооочень грустный
(но это будет оооооочень грустный 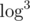 (с большой константой)).
(с большой константой)).
Нет, в этом главная проблема). Ну то есть, ты разбил отрезок [l, r) на
Сама по себе задача о k-ой порядковой статистике на отрезке посложнее, чем просто дерево отрезков декартовых. https://mirror.codeforces.com/blog/entry/2954?locale=ru
С первой частью тоже есть проблема, не понятно как делать push при такой операции.
Написал ерунду, не читайте)
Вроде я придумал как решать за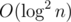 на запрос.
на запрос.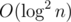 без изменений: отсортируем все пары { a[i], i } по неубыванию, получим отсортированный массив, и по второму элементу в паре(то есть по индексам i) построим MegeSortTree(дерево отрезков, в вершине которого расположен отсортированный массив отрезка, за который отвечает данная вершина). Теперь для запроса k-того элемента нам нужно уметь спускаться по ДО и понимать, в каком сыне лежит ответ. Как это сделать? Если в левом сыне есть хотя бы k чисел из отрезка от l до r, то переходив в него, иначе — в правого новым k, равным разности старого k и количеству чисел от l до r в левом сыне.
без изменений: отсортируем все пары { a[i], i } по неубыванию, получим отсортированный массив, и по второму элементу в паре(то есть по индексам i) построим MegeSortTree(дерево отрезков, в вершине которого расположен отсортированный массив отрезка, за который отвечает данная вершина). Теперь для запроса k-того элемента нам нужно уметь спускаться по ДО и понимать, в каком сыне лежит ответ. Как это сделать? Если в левом сыне есть хотя бы k чисел из отрезка от l до r, то переходив в него, иначе — в правого новым k, равным разности старого k и количеству чисел от l до r в левом сыне.
Давайте вспомним решение за
Ок, я утверждаю, что мы можем переделать нашу структуру так, чтобы мы могли ее изменять. Для этого потребуется быстро перестраивать наш отсортированный массив пар, и, соответственно, ДО, которое мы построили по нему. Для этого Заменим ДО на ДД по неявному ключу, а в вершине ДД будем хранить еще одно ДД, но уже по ключу, чтобы быстро перестраивать сортированный массив, как в ДО. Итого мы не ухудшили асимптотику, но смогли в изменения.
И как это проверять с ДД?
Если кому-то будет полезно (вряд ли), сдал решение за
O(n * m / 8 + m * sqrt(n)), то есть, запросы модицикации за квадрат, а один запрос порядковой статистики за корень. Там есть вызов функцииstressTest()в начале main, его можно опустить. Может у кого-нибудь получится заставить GCC применить авто-векторизацию в месте, где срезается константа (строки 114-123).Кстати, TL на информатиксе к этой задаче был увеличен в два раза.
Как-то так. Правда работает чуть медленнее.
Спасибо. Не думал, что прямо такой цикл сильно не просядет, да еще и с интами. Глянул в ассемблер: gcc заюзал 128-битные регистры + не развернул цикл по несколько итераций. Видимо производительность упирается только в скорость доступа к данным?