awoo's blog

Educational Codeforces Round 57 Editorial
By awoo, history, 6 years ago, translation, In English

1096A - Find Divisible

Tutorial
Solution (PikMike)

1096B - Substring Removal

Tutorial
Solution (Vovuh)

1096C - Polygon for the Angle

Tutorial
Solution (adedalic)

1096D - Easy Problem

Tutorial
Solution (PikMike)

1096E - The Top Scorer

Tutorial
Solution (PikMike)

1096F - Inversion Expectation

Tutorial
Solution (PikMike)

1096G - Lucky Tickets

Tutorial
Solution 1 (adedalic)
Solution 2 (BledDest)
  • Vote: I like it
  • +81
  • Vote: I do not like it

Comments Comments (68)
| Write comment?
»
6 years ago, # |
  Vote: I like it -17 Vote: I do not like it

I solved C differently, also I don't know if it is correct.

Let three chosen points in anti-clockwise order be i_1, i_2, i_3 such that i_1 < i_2 < i_3.

Join (i_1)-(i_3) & let angle it make with (i_1)-(i_1 + 1) be theta and number of vertices between them be x.

Join (i_1)-(i_2) & let angle it make with (i_1)-(i_1 + 1) be phi and number of vertices between them be y.

Using property of polygon(not necessary regular) : sum of interior angle with n sides is (n-2)*180 we can write two equations for theta and phi.

Let alpha be given angle and omega be internal angle of n-gon = (180-360/n).

2*theta + omega*x = (x+2-2)*180 — (1)

2*phi + omega*y = (y+2-2)*180 — (2)

Subtract (2) from (1)

2(theta-phi) + omega(x-y) = 180(x-y)

2*alpha + (180-360/n)(x-y) = 180(x-y)

2*alpha = (360/n)(x-y)

alpha = (180/n)*(x-y)

alpha*n = 180(x-y)

Therefore alpha should be a divisor of 180(x-y) and for minimum n, 180(x-y) should be minimum. Note : Check that for obtained n-gon, its internal angle is greater than or equal to given alpha angle.

→ Reply
»
6 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Please fix B tutorial, where you say about two corner cases. They are swapped.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Yes, they're swapped. I thought about it in reverse order :) Thank you, I will fix it now!

    → Reply
»
6 years ago, # |
  Vote: I like it +10 Vote: I do not like it

Isn't it (cnt(-1))((cnt(-1)-1)/4 in tutorial of F case 1 instead of +1.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Yep, thanks, should be fixed in a couple of minutes.

    → Reply
»
6 years ago, # |
  Vote: I like it +4 Vote: I do not like it

Can someone properly explain task D? So that a beginner can understand you

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it -31 Vote: I do not like it

    Sorry for my irresponsibility

    → Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it +7 Vote: I do not like it

    This is such a basic dp that I'm not even sure what to begin with.

    The way I thought of it was about the following.

    At first, notice that you can check if string has "hard" as subsequence with the greedy strategy. Like take the first 'h', then the first 'a' after it and so on.

    Imagine you have already processed some prefix of s (deleted some characters in it). That means that left out characters have formed some prefix of "hard". What options do you have for the next character? You can either remove it and add ai to the answer or leave it in the string. The second option implies that the current formed prefix of "hard" will be continued with this character (if it equals the next character of "hard").

    Any greedy strategy of removing letters sounds kinda weird (I don't even say that the correct doesn't exist, who knows). However, dpn, 5 is pretty straightforward. Those described transitions are easily done in this dp. And the answer will be the best of all states with n characters of s processed and string "hard" unfinished.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it -6 Vote: I do not like it

      I thought of a different approach but couldn't code it up due to time constraints. Basically, my approach was to delete all occurences of any of the 'h', 'a', 'r', 'd' characters that contribute to the 'hard' subsequence (i.e. delete one of the 4 characters fully so you can't form the subsequence).

      Notice, how I said contribute to the 'hard' subsequence. In 'hhardh' , the 'h' at index 5 does not contribute to 'hard' subsequence so it shouldn't be deleted.

      Now, how do you find the characters which contribute to 'hard' ? Maintain, an array (i.e. every index will have its own array) at every index which store previous indexes of characters which contribute to 'hard'. For eg: At index 0, 'h' does not need any previous characters (since it is start of 'hard') At index 1, array is empty as well ('h') At index 2, array will contain 2 values of previous character (0, 1 since these indices have 'h' in it and 'a' is after 'h') At index 3, array will contain 1 value (2 for previous occurence of 'a') and so on. After this, find all occurences of 'd' and go through each of its value and delete all occurences of one of 'h', 'a', 'r', 'd' . (Keep in mind for conditions like 'hardhard' where 2 mutually exclusive 'hard' are possible)

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
        ← Rev. 3   Vote: I like it 0 Vote: I do not like it

        But there are cases that this will not answer correctly, like:

        6 harard 10 1 10 10 1 10

        You can delete an 'a' and a 'r' with cost equal to 2, and get 'hrad'. You will get a valid solution with your greedy idea, but possibly not the best (the minimum).

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it -6 Vote: I do not like it

          I would delete either the ‘h’ or the ‘d’ since their sum would be 10. As I’ve said, I delete only 1 character fully from the string so I wouldn’t ever delete 2 different characters (like ‘h’ and ‘d’ at the same time). Just the character which has minimum sum

          → Reply
          • »
            »
            »
            »
            »
            »
            6 years ago, # ^ |
              Vote: I like it 0 Vote: I do not like it

            I understand, but this will not give correct answer since you can get cost 2 from the case I told

            → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Hi PikMike,

      I'm not sure what you mean by this line:

      "Otherwise we either change the letter, or let it stay as it is (and the length of the prefix we found so far increases): "

      The corresponding line in your solution code: dp[i + 1][j] = min(dp[i + 1][j], dp[i][j] + a[i]);

      ^^^ Can you tell me 2 things in that line of code:

      1) Why isn't it "j+1" ? Could you clarify that a bit more please ?

      2) There doesn't seem to be any check if the current character (s[i]) is one of {'h','a','r','d'}. Logically speaking, why would you want to remove/delete something that's not one of them ?

      I'm struggling to understand the solution tbh, is there any standard problem similar to this ?

      Thanks!

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        It's the other transition in my code, not this one. And there j is increased if si = "hard"j

        → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        It is simple .All you need to do is to think whether to remove character at current index or not.

        Lets say at current index charcter = 'd'.

        CASE 1 : If we remove it ,then we will add cost of removing current character (cost[i]) to cost that we have calculated till its ('d') last occurence.


        dp[i]=cost[i]+dp[last_occurence_of_current_character]

        Eg. hardhadrhard

        let say i am at last character and want to remove it, then the cost calculated after last occurence of current character(i.e 'd') should not be included in ans because that will never form any "hard" subsequence without this 'd'.Same is the case with 'h','a','r'.

        CASE 2: If i want to keep that character('d'),I need to make sure that somehow i will break that hard sequence(but this time i cannot do anything with this 'd') .so i will go to the previous charcter in "hard" sequence and will add the cost calculted till that index.

        (for eg. if my current charcter is 'd',i will go to last 'r' and compare it with my ans of CASE 1).

        NOTE: In case of 'h'.You have no previous character(since it is the first character of "hard".Then will just add cost of all 'h' that you have traversed till current index).

        My dp state is different and i have not used any 2 d dp

        Check my submission here

        → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      that sounds like a 0-1knapsack approach, is it so?

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        No, I was not maintaining cost for every prefix at every index.The length of prefix is implicit in dp.If current character is 'd' ,it means minimum cost to avoid making "hard" , if current character is 'r' it means minimum cost to avoid making "har" and so on.

        → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Not even 0-1, actually. You are kinda paying for throwing the item out of knapsack, instead of paying for including it.

        → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      PikMike can you explain this part of your code forn(i, n) forn(j, 4) { dp[i + 1][j + (s[i] == h[j])] = min(dp[i + 1][j + (s[i] == h[j])], dp[i][j]); dp[i + 1][j] = min(dp[i + 1][j], dp[i][j] + a[i]); }

      → Reply
  • »
    »
    5 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    include <bits/stdc++.h>

    using namespace std; int main() { int n; cin>>n; string s; cin>>s; long long int A[n]; for(int i=0; i<n; i++) cin>>A[i]; long long int no=0,h=0,ha=0,har=0; for(int i=0; i<n; i++){ if(s[i]=='h') no+=A[i]; if(s[i]=='a') h=min(h+A[i],no); if(s[i]=='r') ha=min(ha+A[i],h); if(s[i]=='d') har=min(har+A[i],ha); } cout<<min(no,min(h,min(ha,har))); } I have a simple answer. basically, what i am doing is checking the cost of sequence(null,h,ha,har) and try to minimize them. variable "h" is storing the minimum cost requires to make the sequence(h) out of string s. so, when we encounter "a" we take the min of cost require to make sequence null and sum of previously stored value of h + cost require to remove that "a" and so on. and ofc we are ignoring every character except(h,a,r,d);

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Very confused about 1096E, why g(s, p, m) = dp(s, p, m)?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Try googling for "Stars and Bars" problem, it should help.

    → Reply
»
6 years ago, # |
← Rev. 5   Vote: I like it +20 Vote: I do not like it

To problem E, it can also be shown that the complexity is O(s2).

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    How can this be shown?

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 4   Vote: I like it +7 Vote: I do not like it

      After fixing Hasan's score, denoted by i, the number of top-scorers is at most (the case where i = 0 is trivial so i > 0 is assumed). And for each g(s, p, m = i), there are 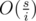non-zero terms in the summation formula. Thus the total complexity is 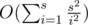, which is also O(s2).

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Ah, yeah, thanks. If only I coded it in a way that the solution would have that complexity :D

        → Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it +1 Vote: I do not like it

in tutorial for problem C. whats the logic behind writing "Since GCD(180/g,ang/g)=1, then 180/g must divide n. Analogically, ang/g must divide k"

can't it be reverse, like n must devide 180/g or not devide it at all, instead k devides both n and ang/g.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +1 Vote: I do not like it

    At first, to clear possible misunderstanding: a divides b means that b = k·a.

    At second, let's look at equality ax = by where (a, b) = 1. Then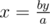 and x is integer, but b is not divisible by a, so y must be. In the same way, 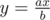leads to fact, that x is divisible by b.

    → Reply
»
6 years ago, # |
← Rev. 3   Vote: I like it +25 Vote: I do not like it

To help with some who is not able to understand the editorial for E. I'll restate it in this way. Enumerate on the score t of Hasan and the number of players cnt that share the same score with Hasan. Then the remaining problem is to count the number of solutions x1 + x2 + ... + xp - 1 - cnt = s - (cnt + 1)t, satisfying that 0 ≤ xi < t.

To make this subproblem more clear, our goal is to count the number of nonegative solutions to x1 + x2 + ... + xn = m, satisfying xi < s. If we can solve this subproblem in O(n) time, then the original problem can be solved in O(sp2) time.

So basically, how can we solve this subproblem? If without the xi < s constraint, then the number of solutions is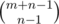 . This is derived by a multiset counting formula. To let it make sense, the number of positive solutions to x1 + x2 + ... + xn = m is 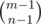, which is equal to the number of ways of inserting n - 1 bars between m objects. And the number of nonnegative solutions to x1 + x2 + ... + xn = m is equal to the number of positive solutions to x1 + x2 + ... + xn = m + n, which is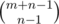

And when we have the constraints that xi < s, we need to use inclusion-exclusion principle. Say if there are i variables that exceeds the limit, i.e., with value  ≥ s, then the equation would become x1 + x2 + ... + xn = m - si, and the number of nonnegative solutions to that equation is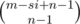 . So, with the help of inclusion-exclusion principle, the answer to that subproblem is

.

Hope that is clear to you enough. If you want to solve that subproblem, here's a link: Character Encoding

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    How to solve these equations when variables have coefficient?

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      That greatly increases the difficulty, which makes the problem generally much harder to solve, if without small constraints and some other special properties.

      → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    I didn't get the last paragraph. Can you please explain how you got the above above by using inclusion exclusion principle?

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Need help in understanding 1096G, I'm only able to understand the first para properly

→ Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

In problem G why is this true?:

"So, if we exponentiate these values, we get a set of values of exponentiated polynomial in the same points."

I mean if you have point-value representation of a polynomial P(x), eg: (x1, P(x1)), (x2, P(x2)), ..., (xn, P(xn)) why point value representation of P(x)k is (x1, P(x1)k), (x2, P(x2k)), ..., (xn, P(xn)k), note that degree of P(x)k is k * deg(P).

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    Shortly, it's math induction.

    For the basic case (number of digits is 1) it's kinda obvious.

    Then, suppose it's true for z digits. Let's prove it for z + 1 digits.

    . Let's rewrite it as follows: , where ci = 1 if i is allowed, or 0 if i is not allowed. But that's the same as if we multiplied two polynomials: one being f(x), and the other being the polynomial having values of dpz as coefficients. But we already assumed that this polynomial is (f(x))z, so the result is (f(x))z + 1.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      That is not what I'm asking, I'm talking about why doing NTT then exponentiating each image of polynomial in point-value form and doing Inverse NTT works, check my edited comment below.

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +11 Vote: I do not like it

        Okay. Recall that Discrete Fourier Transformation gives us a set of polynomial values in some points. We don't actually care which are these points, but if the number of points is greater than the degree of polynomial, then we may restore it back.

        How do we multiply two polynomials f(x) and g(x)? We apply transformation to them, getting a set of values of the first polynomial in some points, and a set for the second polynomial. Then we multiply these values, obtaining the values of polynomial f(x)g(x) in the same set of points. And then we apply inverse transformation.

        Exponentiation is kinda the same. Apply the transformation, get a set of values in some points. Then raise these values to the desired power. And then apply inverse transform. But to be able to get the result, we have to apply transformation on d + 1 points, where d is the degree of resulting polynomial, not the one we exponentiate.

        I am not sure if it works with complex FFT since there may be precision errors, but with NTT it is perfectly fine.

        → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Also why in editorial are saying that NTT with binary exponentiation is , shouldnt this be ?

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +19 Vote: I do not like it

        if implemented correctly. The last iteration multiplies two polynomials of size , second to last — two polynomials of size , and so on.

        → Reply
»
6 years ago, # |
← Rev. 3   Vote: I like it +25 Vote: I do not like it

Hello, E is solvable in O(p)!!! (wow, very short complexity!!!)

Here is my code: https://mirror.codeforces.com/contest/1096/submission/47655644 Here is my solution:

We want the number of ways that the first person wins, when he gets  ≥ r

if u consider the number of ways where at least one person gets  ≥ r, then some guy must win, and the first guy will be that person with probability

so the number of ways that the first guy wins (and therefore has  ≥ r since at least one person has  ≥ r) is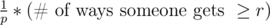

so answer is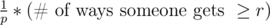 divided by total possibilities which is (# of ways first dude gets  ≥ r)

The number of ways someone gets  ≥ r can be calculated in O(p) with Principle Inclusion Exclusion!

The number of ways first dude gets  ≥ r can be calculated in O(1) with Stars and Bars

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    Good catch! That's absolutely a better way to interpret the problem. Thanks!
    But currently with these constraints only 26 contestants came up to a solution! Imagine if we had set constraints for a linear time solution! :)))
    Btw, I think you'd better say it's O(s+p) because you had a factorial pre-computation which is done in O(s).

    → Reply
»
6 years ago, # |
  Vote: I like it +42 Vote: I do not like it

Please, could someone explain solution to problem G in linear time with no Fourier.
I see, at least four users (Dmitriy.Belichenko indiewar FizzyDavid Emma194) got OK using this approach.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +66 Vote: I do not like it

    We need to calculate the nth power of a low-degree polynomial P.

    A(x) = Pn(x)

    A'(x) = nPn - 1(x)P'(x)

    Unable to parse markup [type=CF_TEX]

    A'(x)P(x) = nA(x)P'(x)

    Thus we get the recurrence relation of the array.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +11 Vote: I do not like it

      This solution is amazing. The code is very short and it runs fast. But indiewar just copied FizzyDavid's code.

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +10 Vote: I do not like it

        I'm sorry...I just want to find a good template of NTT.Then I saw this amazing solution,and I copied it.It's an evil thing to just copy others' code.I'm very sorry.

        → Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it -11 Vote: I do not like it

Huh,

I didn't realized that using fast multiplication algorithms within fast exponentaion algorithm mitigates log(N) from fast exponentation under proper analysis and proper implemenation. So I've though Schonhage–Strassen would give O(N·log2(N)) instead of O(N·log(N)) and Karatsuba will give O(Nlog23·log(N)) instead of O(Nlog23).

And O(Nlog23·log(N)) is worse than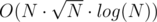 that is pretty desperate to fit in TL. But now I think that O(Nlog23) might be good enough. So, is there anyone who solved G with Karatsuba?

By the way, second solution from editorial is really cool!

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Div 2 c , i am not able to understand the last line where it says if k = n-1 , we have to take x = 2 , but why ? if x = 1 and ang/g = n-1, then k = n-1 but that is incorrect as 1<=k<=n-2 , if we take x=2 then k = 2*(n-1),which i think should also be wrong as it does not come in range of k, i am bit confused about this, could anyone please clear it.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it 0 Vote: I do not like it

    If x = 2 then k' = 2(n - 1) = 2n - 2 and n' = 2n, so k' = n' - 2 and it's okay.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
      ← Rev. 2   Vote: I like it 0 Vote: I do not like it

      Correct me if i am wrong but i think the code provided in the editorial for Div2 c is wrong as for the input

      2 180 0

      it prints the answer as 1 and 2 but in the question it is given that answer can range from [3 , 998244353]. Also, value of k can be equal to n if we put ang = 180 and editorial doesn't mention anything about that.

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        If you'd read problem statement, you'd see that 1 ≤ ang < 180.

        → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

my solution for D is exactly similar like editorial but still getting WA can someone help 47725623

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it +3 Vote: I do not like it

    Try something like this. (first edit of comment contains the bug itself)

    4 hard 1 1 1 1

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

In problem F, couldn't get the meaning of P.Q^-1 (mod 998244353). Can anyone please explain. For the first sample testcase answer is 2.5. So P=5 and Q=2, then how come we get 499122179 .

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    For Q = 2, Q - 1 mod 998244353 is 499122177. So (5 × 499122177) mod 998244353 is 499122179. I hope you understand what Q - 1 mod 998244353 means. If not, look for "modular inverse".

    → Reply
»
6 years ago, # |
  Vote: I like it +3 Vote: I do not like it

Can anyone please explain what the following function does in problem F??

int f[N];

void upd(int x){ for (int i = x; i < N; i |= i + 1) ++f[i]; }

int get(int x){ int sum = 0; for (int i = x; i >= 0; i = (i & (i + 1)) — 1) sum += f[i]; return sum; }

→ Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Not particularly proud of it, but it's possible to squease an O(s*r*p) solution past the time requirements.

→ Reply
»
5 years ago, # |
← Rev. 2   Vote: I like it 0 Vote: I do not like it

Well I had a greedyish DP approach for D which got accepted.

Suppose while traversing the string, we reach a one of the characters of "hard"

Suppose the character is 'a' , then we have the option of removing the 'a' or we can remove all the 'h's that came before the 'a'.

Similarly for 'r', we can delete 'r' or delete all the 'a' that came before it(note here we are not considering the 'h's that came before the 'r' because we have considered 'h' for the 'a's)

Similarly for 'd', we can delete 'd' or delete all the 'r' that came before it(note here we are not considering the 'h's and 'a's that came before the 'd' because we have considered 'a's for the 'r's and 'h's for the 'a's that came before)

The choice to delete the characters will depend on the values they hold. So, whether we will delete the current 'a' or the 'h's that came before ,will depend on the value of the current 'a' and the sum of values of 'h's that came before, we can store these using dp.

Then we can just print the minimum value stored in the last dp state,i.e dp[n-1]

Link to the code: Accepted Solution

→ Reply
»
5 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I find it hard to understand C.

"Any possible angle in the n-gon is a inscribed angle in the circle and equal to half of central angle."

What does this mean? What is the central angle? Which relevance (and meaning) has the word "inscribed" here?

→ Reply