hmehta's blog

Topcoder SRM 746 and Editorials
By hmehta, history, 6 years ago, In English

Topcoder SRM 746 is scheduled to start at 12:00 UTC -5, Jan 15, 2018. Registration is now open for the SRM in the Web Arena or Applet and will close 5 minutes before the match begins

Editorials: https://www.topcoder.com/blog/single-round-match-746-editorials/

Problem Writer: majk CF:majk

This is the fourth SRM of Stage 2 of TCO19 Algorithm.

Stage 2 TCO19 Points Leaderboard | Topcoder Java Applet | Next SRM 747 — January 19

Hope to see most of you competing! All the best!

  • Vote: I like it
  • +49
  • Vote: I do not like it

Comments Comments (39)
| Write comment?
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

Match Begins in less than 4 hours from now!

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it -6 Vote: I do not like it

    hmehta do some codeforces please. You are orange in topcoder. You can easily can be orange here also :)

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +53 Vote: I do not like it

      Hey, I am orange on Topcoder, because Topcoder Admins are orange there.

      Not in that good touch anymore these days, very hard to come back and compete with much more better programmers like you guys these days! Happy administrating and promoting/motivating members for CP wherever possible now :)

      → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +2 Vote: I do not like it

    Match begins in 2 hours from now!

    → Reply
»
6 years ago, # |
  Vote: I like it +85 Vote: I do not like it

I'm sorry but what's this 1000...

→ Reply
»
6 years ago, # |
  Vote: I like it +16 Vote: I do not like it

The problem setter of Div1C should stop creating problems.

→ Reply
»
6 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Hi majk can you please stop creating problems like 1000 =)? Are you happy with posing that problem? What lead you to posing a trivial question that 1) requires 3D library, 2) NEEDS THAT LIBRARY TO BE IMPLEMENTED ON FREAKING BIG INTEGERS? Thank you for your attention, I should have listened to my friend who didn't participate because of a problemsetter and tried to warn us.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +22 Vote: I do not like it

    Well, this is too scalar and one vector products, not too much hard. Or just minimize bilinear form. Normal problem for icpc contest (if drop originality issue), but really strange as most (and only) hard on 1:15 contest.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it -8 Vote: I do not like it

      Yeah, that geometric part is not that complicated, but what's the point of big integers?

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +8 Vote: I do not like it

        Probably, that's the only way to forbid ternary searches. Also, as rng_58 showed, __int128 is enough if doing things in correct order. I agree, most hard for me, was to understand what python wants from me in arena's editor, but probably, that's a problem with i don't good enough with choosing good tool, not anything else.

        → Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +16 Vote: I do not like it

    Well I certainly can. Should I? :)

    To answer your questions:

    Firstly, I considered that the thinking part of 1000 more difficult than it turned out to be. From the past contests I've written I tried to limit myself regarding the difficulty and this time it seems it was a bit too much on the easy side.

    Secondly, master solutions have to be written in Java, which is not my primary language. Hence I didn't use any library myself. Having a good prewritten library helps, but so does for flows, segment trees or suffix arrays, right?

    Thirdly, I thought that some basic handling of precision issues complements the problem. I wanted to give you every indication possible that the precision matters. The limits are quite unusual for a geometric task. The third sample fails miserably on doubles. It is a case of two almost parallel lines, where catastrophic cancellation happens. Changing this to long double and just hoping it will pass is a risky strategy. You don't even need arbitrary precision integers, __int128 works fine on Topcoder.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +10 Vote: I do not like it

      Well, I actually have no problem with first and second point, but third one drives me mad. "I thought that some basic handling of precision issues complements the problem" — seriously, wtf? You know what is basic handling of precision issues? When a slight misprecision can cause different flow of execution by going into some if or not, or when we are doing computations where some catastrophic cancellation happens and we are able to get rid of it or when we are doing silly things like in some cases we multiply/divide x and y by 10^10 just before passing it to atan2. Going through all the code, thinking whether all computations are doable on ints and if not then coming up with a different way of doing them and then changing int to bigints is not "basic handling of precision issues", that's a freaking last resort while screaming for help.

      Btw regarding "The third sample fails miserably on doubles. It is a case of two almost parallel lines, where catastrophic cancellation happens. Changing this to long double and just hoping it will pass is a risky strategy. " — 1) I handled parallelity check on ints as it is the only "binary" decision to make, all others are "continuous" and don't affect flow of execution, just some real numbers are some other real numbers, and that should be even more than enough for a sane problemsetter 2) I don't know who uses doubles in geometry by deafult, but that's not a wise thing to do and I am not one of those people. Tbh I didn't even look at constraints when coding this problem since I assumed that setter is not an evil and insidious man, but unfortunately I was not right and when I have solved all problem and 25 minutes remained and I had nothing else to do I opened it once again and noted "coordinates are up to 10^12" and I already knew that my solution may not pass and I made sure it won't within remaining time.

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +18 Vote: I do not like it

        ... but third one drives me mad.

        Understood and noted. I generally don't want to drive you mad.

        ... or when we are doing computations where some catastrophic cancellation happens and we are able to get rid of it ...

        In this case you should also be able to prevent the catastrophic cancellation by reordering the summands (in the point-plane distance calculation). Does that qualify?

        that's a freaking last resort while screaming for help.

        Sorry, only thing I can picture now is a screaming marmot frantically looking up the documentation on BigInteger while the timer is running out.

        I handled parallelity check on ints as it is the only "binary" decision to make, all others are "continuous" and don't affect flow of execution ...

        True, but it is also a well known fact that computing the intersection of two almost parallel lines is tricky. So is, for instance, getting the distance of two skew lines. Binary decisions are the calculations that you absolutely must care about, but that doesn't mean that the rest always rounds in your favor.

        I'm not denying that I expected the task to turn out a bit differently, I'm merely explaining my reasoning during problem setting.

        → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +62 Vote: I do not like it

      Please don't stop creating problems. I generally like your problems. Today's 250 was easy but quite nice. I also think 1000 was a good problem except for the precision limit. It requires some observation: first we need to reduce the problem to the distance between a point and a plane spanned by two vectors, then we need to find that this is the ratio between the volume of certain tetrahedron and the area of certain triangle. For me it looks more like a 500, but it's always hard to estimate the difficulty.

      However the tight precision limit looked annoying. SRM 400 hard also required very high precision. The difference is that this problem requires an observation to get high precision, while today's problem requires just technical transformation (for example we can convert everything into BigDecimal in Java without any thinking, and most submissions should pass). I prefer to make problems harder idea-wise (and not by asking knowledge of language or increasing the amount of typing).

      For example, in today's set, we can swap 500 and 1000, lower the limit of the geometry task, and raise the limit of the string task (n ≤ 109, length ≤ 105). Doesn't it look like much more interesting?

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +8 Vote: I do not like it

        ... raise the limit of the string task (n ≤  109,  length ≤  105). Doesn't it look like much more interesting?

        It does, but unfortunately that's too big of an output for Topcoder to handle. Furthermore, how do you write the checker? Is it as straightforward as Manacher?

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it +18 Vote: I do not like it

          Flip characters at even positions, and count the number of palindrome substrings of even lengths, using Manacher.

          → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it +2 Vote: I do not like it

          Counting antipalindromes in binary string is the first task ever that I did on an official competition. It's exactly the same as Manacher but with == changed to !=

          → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +26 Vote: I do not like it

        To make myself clear, I didn't ask him to stop creating any problems. I asked him to stop creating problems like today's 1000

        → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
        ← Rev. 2   Vote: I like it +26 Vote: I do not like it

        An alternative reduction for Div1 Hard.

        In the reference frame of the first probe, the second one can move along the line parallel to and the planet can move along the line parallel to 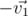. The problem is now a textbook exercise to find the distance between two lines in 3D.

        → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it -13 Vote: I do not like it

      Btw, you could have requested an answer as a rational number that is square of an answer. That would have been much better problem. But of course still much worse than setting reasonable constraints.

      → Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it +43 Vote: I do not like it

    To me it seems that today's 1000 actually penalized those who have a 3D library, as you're unlikely to have big integers there, and when you have a kitchen sink of methods calling one another porting to big integers is not always straightforward.

    When I look at the five passing solutions, four or maybe all five seem to be written from scratch (mine definitely is), and required an understanding of what cross and dot products are in 3D to come up with a very short implementation which is easy to port to big integers.

    Of course, it's easy to say things like this from the first place, but I think this problem is fine, and the low constraints in 500 are also fine since I perceive allowing random shit (c) to pass in this problem as a positive instead of a negative.

    → Reply
»
6 years ago, # |
← Rev. 2   Vote: I like it +16 Vote: I do not like it

My solution for 500 in a nutshell:

1) generate random string of random length up to 100

2) replace random prefix with "abababab..." to randomly increase amount of antipalindromic substrings

3) repeat unless you have all answers

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +16 Vote: I do not like it

    just generating random string with 9/10 probablity of changing symbol passes in less than 1 second. No idea why.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +16 Vote: I do not like it

      String "ababab...ab" of length 2n has n2 antipalindromic substrings. So you are almost subtracting sum of some random squares(actually you add a bit more strings but that doesn't matter much).

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
        ← Rev. 2   Vote: I like it +3 Vote: I do not like it

        With a similar idea, if n = x2 + y2 for some x, y we can achieve n with the string:

        .

        Maybe some smart generalization of this idea can be used to find a non heuristic solution? (I wanted to use the fact that every natural number can be written as the sum of 4 squares)

        → Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it +34 Vote: I do not like it

    My solution is simple: Just concatenating "babab....ab". Each has i(i + 1) antipalindromic substrings and concatenating adds zero antipalindromic substring.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      This is exactly what I was looking for. Thank you!

      → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      What does it mean for a string to be antipalindromic? just regular not palindrome? if yes, what does i denote here?

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +3 Vote: I do not like it

        Bekh:

        An antipalindrome is a string which differs from its own reverse at all positions. For instance, "ab", "aabb", "abab", and "abbaab" are antipalindromes, whereas "aaab", "abba", "aababa", "baa", and "a" are not (I copy & pasted the problem statement).

        In this problem you are given a number 0 ≤ n ≤ 1000 and you have to build a binary string of length up to 100 that has exactly n substrings that are antipalindrome

        The idea in his answer is to define a block of size i as the string

        .

        This string has i(i + 1) substrings that are antipalindrome (since all substrings of even lengths are antipalindromes and a substring of odd length can never be an antipalindrome).

        The last idea he says is that when you concatenate two blocks, an antipalindrome susbstring must be completely contained in some block (if a substring contains the two succesive b's there is no two succesive a's that could possibly form an antipalindrome), hence the amount of total antipalindrome substrings in the concatenation, is the sum of antipalindrome substrings in each block.

        I hope you find the explanation useful.

        → Reply
        • »
          »
          »
          »
          »
          6 years ago, # ^ |
            Vote: I like it 0 Vote: I do not like it

          That was perfect explanation. Thank you.

          → Reply
»
6 years ago, # |
  Vote: I like it +10 Vote: I do not like it

Why were constraints in 500 so low? You could have easily asked about n up to 10^10 or at least 10^6 and no random shit would pass. Inb4, arena should handle returning string up to 2000 characters, right?

→ Reply
»
6 years ago, # |
  Vote: I like it +35 Vote: I do not like it

My screencast: https://youtu.be/EhkGX648sNI

→ Reply
»
6 years ago, # |
  Vote: I like it +1 Vote: I do not like it

Does anybody have a solution for div 2 1000 problem other than the one mentioned in the editorial? or know a proof for why this solution works or a tleast the intuition behind it?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +3 Vote: I do not like it

    My solution using backtrack + pruning

    https://ideone.com/woBwz6

    I don't have proof for this solution.

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Wow, this actually passes in ~6ms. Number of palindrome substrings increase so quickly which makes this pruning so effective. Nice observation.

      → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it +4 Vote: I do not like it

      Did you tried for all values before submitting or did you took a risk by calculating the answer for a few large values?? Or were you confident that the solution will pass?

      PS:- I am asking because such greedy questions sometimes become hard to solve or even hard to approach.

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it +3 Vote: I do not like it

        I was confident that the solution will pass...but when It passed the sample cases in very fast time , I found that there's high possibility that the solution will pass...also when I was trying in the problem I found that number of palindromic substrings increase very fast as we use two characters only.

        → Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it +3 Vote: I do not like it

    Bekh

    I solved it in a very similar way to the editorial, so I will try to explain the intuition behind it.

    Imagine you have the following string

    Clearly every substring is a palindrome, and it has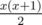 substrings. So, what happens when we start appending b's at the end? we arrive to a string that looks like this:

    A substring that starts in an a and ends in a b can never be a palindrome, hence this string has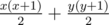 substrings.

    If we follow this procedure we arrive at a string that looks like this (if y > 0):

    A palindrome must start and end with the same letter, so in addition to the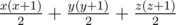 substrings, we must add those starting with an a in the first block and ending at an a in the last block, how many of these do we have? min{x, z}. So we should add this amount to the total of substrings.

    This is the reason behind the formula in the editorial. Of course, there are a couple of other ideas and corner cases (explained in the editorial) that help with the implementation. Since I used a very similar approach (The only difference being that I added another block of b's at the end that ensures no corner case for n = 19) I will not leave my code here.

    Happy coding!

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      Thank you for your response. I wanted to also know the intuition (or proof) behind why the sum of these could get me any number 1~1000.

      → Reply