Usu's blog

Fast exponentiation with big exponent

By Usu, history, 6 years ago, In English

Hey! I have a question. If I have to calculate a pow b modulo mod, with b>mod, is it the same with a pow (b % (mod-1)?

  • Vote: I like it
  • +29
  • Vote: I do not like it

»
6 years ago, # |
← Rev. 3   Vote: I like it +42 Vote: I do not like it

By Euler's Theorem, if gcd(a, n) = 1,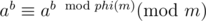 . If m happens to be a prime, then phi(m) = m - 1.

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +11 Vote: I do not like it

    If "gcd(a,n)=1", you mean gcd(a,m)=1? I can not see the n

    → Reply
»
6 years ago, # |
  Vote: I like it +45 Vote: I do not like it

Even when gcd(a, n) > 1, the following holds: If b ≥ φ(m),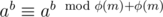 . When m is large and you cannot efficiently factor it to compute φ(m) and b is given in decimal form, you can still use fast exponentiation. Process digits of b one by one starting from the most significant one and use a10b + c = (ab)10 × ac.

→ Reply