Alex_2oo8's blog

Invitation to CodeChef February Long Challenge 2019 sponsored by ShareChat!
By Alex_2oo8, history, 6 years ago, In English

Greetings Codeforces community!

Come participate in CodeChef’s February Long challenge sponsored by ShareChat! This is a 10-day contest that invites participants to solve 7 problems and 1 tie-breaker style challenge problem. The contest is open to programmers of all skill levels. The contest problem statements will be available in English, Hindi, Bengali, Russian, Mandarin and Vietnamese.

Participants of Long Challenge also have an opportunity to apply for job openings at ShareChat — India’s fastest growing social network! Visit the contest link to know more.

I hope you will join your fellow programmers and enjoy the contest problems. Joining me on the problem setting panel are:
- Testers: Alex_2oo8 (Alexey Zayakin), yashChandnani (Yash Chandnani)
- Editorialist: taran_1407 (Taranpreet Singh)
- Statement Verifier: Xellos (Jakub Safin)
- Setters: hmrockstar (Himanshu Mishra), Akil Vohra, Aditya Dimri, Daanish Mahajan, TooDumbToWin (Pranjal Jain), mraron (Áron Noszály), Slow_But_Determined (Abdullah Aslam), Stylianos Kasouridis, Alexander Zhou, Danylo Mocherniuk
- Russian Translator: Mediocrity (Fedor Korobeinikov)
- Mandarin Translator: huzecong (Hu Zecong)
- Vietnamese Translator: Team VNOI
- Bengali Translator: solaimanope (Mohammad Solaiman)
- Hindi Translator: Akash Shrivastava

Contest Details:

  • Start Date & Time: 1st February 2019 (1500 hrs) to 11th February 2019 (1500 hrs). (Indian Standard Time, +5:30 GMT) — Check your timezone.
  • Contest link: https://www.codechef.com/FEB19
  • Registration: You just need to have a CodeChef handle to participate. For all those, who are interested and do not have a CodeChef handle, are requested to register in order to participate.
  • Prizes: Top 10 performers in Global and Indian category will get CodeChef laddus, with which the winners can claim cool CodeChef goodies. First to solve each problem except challenge — 100 laddus. Know more here: https://www.codechef.com/laddu
    (For those who have not yet got their previous winning, please send an email to winners@codechef.com)

Good Luck! Hope to see you participating! Happy Programming!

  • Vote: I like it
  • +53
  • Vote: I do not like it

»
6 years ago, # |
  Vote: I like it +11 Vote: I do not like it

What's the approach to get 100 on MAXTAX?

→ Reply
  • »
    »
    6 years ago, # ^ |
      Vote: I like it +5 Vote: I do not like it

    Decompose the graph into a DAG of SCC's then its a Knapsack-like DP : DP[i][j] = max tax that can be collected till the i'th SCC with j houses left.

    Dp[i][j] = max(dp[i][j], dp[k][j - l] + cost(l)) for all k such that there is a edge from k -  > j and cost(l) is tax you collect by leaving the l lowest values. You can precompute the optimal values for k for each j - l and cost(l) for each i.

    Complexity is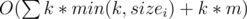

    → Reply
    • »
      »
      »
      6 years ago, # ^ |
        Vote: I like it 0 Vote: I do not like it

      But won't this result in O(N * K^2 + M * K) complexity in a worst case scenario?

      → Reply
      • »
        »
        »
        »
        6 years ago, # ^ |
          Vote: I like it 0 Vote: I do not like it

        Assume each SCC has equal amount of vertices X then the work done is N / X * min(X, K) * K <  = N * K .

        → Reply
»
6 years ago, # |
  Vote: I like it +2 Vote: I do not like it

Can someone share there approach for Xor Decomposition

→ Reply
  • »
    »
    6 years ago, # ^ |
    ← Rev. 2   Vote: I like it 0 Vote: I do not like it

    During the DFS , whenever the subtree xor becomes equal to X or 0 , remove the edge from that node to its parent. Shrink all the forests obtained to a node each and give it a value of 1 if xor was equal to X otherwise 0.Connect the removed edges again, the problem is reduced to finding the no. of partitions of the decomposed tree such that each each forest has an odd sum. This can be done using DP on children. dp[i][0] = no. of ways to get even sum till the ith child.

    dp[i][0]=dp[i−1][0]∗(odd(ci)+even(ci))+dp[i−1][1]∗odd(ci) (the odd case can be derived by swapping 1 for 0) where odd and even store the number of partitions such that the all parts that have been removed are odd and current is odd/even.

    → Reply
»
6 years ago, # |
  Vote: I like it 0 Vote: I do not like it

I have a different solution for TRDST than the one in editorial . As the TL was 5 seconds, I just came with a block decomposition solution. I keep the level of each node using 1 as root of tree . Now to measure the distance from each node u I need to measure level of each node keeping u as root of tree . Initially I have measured the level of all nodes keeping 1 as root , now on keeping any child v of 1 as root, the level of all nodes in subtree of v decreases by 1 while the levels of all other nodes increase by 1. To do this fast, I use block decomposition. I divide the euler array into b = min(100,sqrt(n)) blocks . For each block I keep the count of nodes with levels <= i for i in range(1,1e5). Now to update a range , I just need to add to the lazy component of each block and iterate through the rest of elements whose blocks aren't covered fully . The count array can be modified in O(1) for each element . Now finally using binary search I get the required di.

Space Complexity : O(N*b) Time Complexity : O(N*b*LOG N + (N*N)/b)

This fits into the TL and constraints provided . Sorry for the abrupt description .

→ Reply