| № | Пользователь | Рейтинг |
|---|---|---|
| 1 | tourist | 4009 |
| 2 | jiangly | 3823 |
| 3 | Benq | 3738 |
| 4 | Radewoosh | 3633 |
| 5 | jqdai0815 | 3620 |
| 6 | orzdevinwang | 3529 |
| 7 | ecnerwala | 3446 |
| 8 | Um_nik | 3396 |
| 9 | ksun48 | 3390 |
| 10 | gamegame | 3386 |
| Страны | Города | Организации | Всё → |
| № | Пользователь | Вклад |
|---|---|---|
| 1 | cry | 167 |
| 2 | Um_nik | 163 |
| 3 | maomao90 | 162 |
| 3 | atcoder_official | 162 |
| 5 | adamant | 159 |
| 6 | -is-this-fft- | 158 |
| 7 | awoo | 157 |
| 8 | TheScrasse | 154 |
| 9 | Dominater069 | 153 |
| 9 | nor | 153 |
Given an array a[] = {1, 1 ,1 , -1} . you have to find all the subarrays of the given array whose sum is exactly = k.
example : a[] = { 1 , 1 , 1 , -1 } and k = 1
Ans = 4 all 3 one's + range from [2,4]
There is an geeks_article for it but the explanation is not good and clear and also without proof .
Can anyone explain me how to solve this problem with some explanation !
Thanks !
Use prefix sums. Let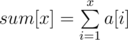
, then the sum of a subarray in [l, r] is equal to sum[r] - sum[l - 1].
If we iterate over all possible pairs (l, r), we get a complexity of O(n2).
Fix the right boundary, if we maintain the prefix sum of the left boundary in a set, the time complexity is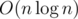
. Note that the possible left boundary is nondecreasing as the right boundary increases, we can handle this with two-pointers technique and thus have a complexity of O(n).
wait...the elements may be negative.
OK, my bad. So ignore the nondecreasing thing.
We can still get $$$O(n)$$$ if we assume hash tables work in $$$O(1)$$$
What to do if i need Positions as well. Means left and right pointers of the required subarry.
use a map<int,vector> to store to maintain the left boundary, this mean that instead of using a count you will maintaing the indices where the prefixes sums of a value ocurred, the complexity changes to $$$O(n log n + S)$$$, where S is the numbers of pairs that sum exactly k. That shoundn't be a problem because if you need all the pairs, you should have the time to at least store all the pairs and print them.
In this case, ai isn't necessarily non-negative, so the two-pointer solution doesn't work. You could use a hash table instead of a set to achieve expected O(n) time.
yes , the elements may be negative , 0 or postitive and we have to device a linear complexity.
how to do so ?
Fix the right bound and store the first r prefixes into a bucket.Then ans should be increased by bucket[k - sum[r]].If we use
.If we use 
!)
mapthe complexity will beunordered_map(only allowed in C++11 or higher versions) it will be O(n).If we use a hash table then it will be expected O(n).(Sometimes it may be even slower thanA simple solution is to traverse all the subarrays and calculate their sum. If sum is equal to the required sum then increment the count of subarrays. Print final count of subarrays.