The Editorial of the First Codeforces Global Round

6 years ago, # ^ |

+37

Corrected thanks!

We indeed increased constraints slightly before the contest.

→ Reply

lamda_cdm

4 years ago, # ^ |

Can you point me to where I am wrong in the third question? My approach was somewhat like this I took the intervals of the numbers ie A[i]-A[i-1] and stored them in one vector and sorted them in decreasing order Now I can make 'K' tape which means I can use K-1 use non attached tapes right... so I took the sum of all the intervals and deleted the first k-1 larger intervals from the sum that is sum-v[0]-v[1]-..v[k-2].. and then printed out (sum+k) as the final answer I got stuck in the test case number 9 ... Thanks in advance for your help.

→ Reply

Zenkai

6 years ago, # |

+28

Probably one of the most well written editorial i have ever seen!

→ Reply

6 years ago, # |

Can someone please explain the solution of B in more detail?

→ Reply

mu.shakhawat.hossain

6 years ago, # ^ |

Suppose, We have a stick with 100 cm length and 8 broken points,

.........10.12.... .....30....35..... .......80.....86......93.........100...

Since, there are 8 broken points and each point takes 1cm, at the very least we need 8cm tape to fix them. But with the constraint of number of tapes, we will have to cover a segment instead of a point. In the process, we will end up covering some unbroken points. So, total covered points will be the broken points + the points which fall under those segments that we picked to cover due to the constraint.

Consider the following cases -

Case 1: k = 8

We have 8 tapes to use. So, there is no point wasting tape on unbroken points. Just cut 8 tapes of 1 cm, and fix the broken points. So, we are only using 8 cm of tape, no tape wasted. Cool!

Case 2: k = 7

We have 7 tapes to use. Now, we are 1 piece short. So, we will fix a segment with one tape (instead of just a point) and for rest of the broken points we can just put 1cm pieces.

So, how do we choose that special segment? The goal is to waste as little as possible tape. Looking at the pipe above, we would like to cover 10.12, just wasting a 1cm tape. This will make us to cover point 11 which is not broken. But there is no better way.

So, how much tape we are using now? 8 broken, 1cm points + 1 extra 1cm point = 9cm

Case 3: k = 6

We have 6 tapes to use. Using the same approach on Case 2, we have to pick another segment. 30....35 is our next best option, because we are justing wasting 4cm tape in the middle.

Thus 8cm legit broken points + 1cm in the middle of 10.12 and 4cm in the middle of 30....35 = 13 cm

So, we will be needing to cover up the short amount of tape, and we will choose the segments which come with little waste of tape. To find those segments, we need to list all b[i+1] — b[i] — 1, meaning the lengths of non-broken segments. Now, we will just cover the smallest (n-k) of the segments we need to.

→ Reply

6 years ago, # ^ |

Thanks!

→ Reply

6 years ago, # |

Thanks for fast tutorials

→ Reply

patelparth5686

6 years ago, # |

can someone explain tape (2 question) in better way

→ Reply

Virus_HKG

6 years ago, # ^ |

hey I will explain it with help of one example; let n=10, n=35, k=5; b[i]={1 2 5 6 9 11 13 15 23 27} broken segments; 1_2__5_6___9__11__13__15________23___27_ (where you have to repair I have put that integer no.)
if you have value of k more than n (k>n), then you can easily cut the 10 segment of 1cm so it will very less tap require(only total 10cm tap required=10cm(1cm+1cm+1cm+1cm+1cm+1cm+1cm+1cm+1cm+1cm). But here the value of k is 5 so you have to cut 5 segment such that all broken part should cover.
1_2__5_6___9__11__13__15________23___27_ (where you have to repair I have put that integer no.)
now if you cut 1cm of 10 segment tap it is less tap required but you can cut only 5 tap segment because k value is 5.
so you will cut 5 segment such that segment cover max length with small tap. now a[i]=b[i+1]-b[i] So a[i]={1,3,1,3,2,2,2,8,4} so by sorting it a[i]={1,1,2,2,2,3,3,4,8} So you will repair first all that segment which are very near means 1 and 2, 5 and 6, and so on.. you can cut the tap at most five times(k value), so your target is with this five segment you have to repair the stick.

→ Reply

koval.victor

6 years ago, # |

Now consider the case when a=2x−1. This implies (a⊕b)+(a&b)=a, hence it's sufficient to find the largest proper divisor of a — it will be the desired answer.

Why is that implied in this case?

→ Reply

6 years ago, # ^ |

When a=2^x-1,it's binary will have all bits as 1.So, a&b equals b and (a xor b) equals a-b.

→ Reply

koval.victor

6 years ago, # ^ |

Thanks for quick response!

Why is the largest proper divisor the answer? Does it relate to the Extended Euclidean algorithm?

→ Reply

6 years ago, # ^ |

Notice that when b is divisor of a,a-b will also be the divisor of a. So,maximum possible gcd(a-b,b)=largest divisor of a.

→ Reply

aboAdnan

6 years ago, # ^ |

← Rev. 3 →

I think you meant that, when b is a divisor of a, a - b will be divisible by b, didn't you?

→ Reply

6 years ago, # ^ |

Oh...Yes

→ Reply

c4big2

6 years ago, # ^ |

gcd(a-b, b) eqaul to b when b is factor of a.

→ Reply

lamda_cdm

4 years ago, # ^ |

→ Reply

chemthan

6 years ago, # |

+21

I expected more than on G. Since it is just working with cases. The idea is obvious.

→ Reply

6 years ago, # ^ |

+29

Well, yes, but there are several cute ideas along the way (that the degrees are small and and the idea about reducing the problem to uncolored vertices only, which is not mandatory to get AC, but helps greatly)

→ Reply

patelparth5686

6 years ago, # ^ |

-9

can you explain part B

→ Reply

6 years ago, # ^ |

+30

But there is an editorial written already...

Ask some concrete question at least.

→ Reply

6 years ago, # ^ |

What I want to know is, why have people stored the differences as b[i] — b[i — 1] — 1 and added n to the answer?

→ Reply

6 years ago, # ^ |

Looks fine to me, basically you need to spend tape to cover the broken segments themselves ( + n in the end) and then you only care about which gapes between segments are "collapsed" into single tape part and which are not.

→ Reply

6 years ago, # ^ |

Got it, thank you!

→ Reply

lamda_cdm

4 years ago, # ^ |

→ Reply

rebornplusplus

6 years ago, # |

+21

Anybody solved D with greedy?

→ Reply

dodobhoot

6 years ago, # |

In D, Can you please explain the statement — So we can assume that there are at most 2 triples of type [x,x+1,x+2] for each x.

→ Reply

6 years ago, # ^ |

← Rev. 3 →

It means that given some x, it isn't necessary to try choosing the triplet [x, x+1, x+2] more than 2 times. Because for k > 2 (assume km = k mod 3), k[x, x+1, x+2] is equivalent to km[x, x+1, x+2] +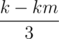 $\text{[math]}$ [x, x, x] + 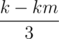$\text{[math]}$ [x+1, x+1, x+1] + 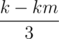$\text{[math]}$ [x+2, x+2, x+2].

→ Reply

atlasworld

6 years ago, # ^ |

← Rev. 2 →

what do you mean by it doesn't make sense ? what will happen if we choose triplet (say) 3 times ?

And how dp state is formulated ? can you describe a little bit.

→ Reply

6 years ago, # ^ |

As k[x, x+1, x+2] is equivalent to km[x, x+1, x+2] + (k-km)[x] + (k-km)[x+1] + (k-km)[x+2], you can use this observation to apply simple dp that tries to take a triplet [x, x+1, x+2] at most only 2 times, and gives you the same optimal answer.

→ Reply

atlasworld

6 years ago, # ^ |

so , in the optimal answer there will be no triplet like [x,x,x] ?

do we have to form triplets only using [x,x+1,x+2] . only it will give optimal answer ?

→ Reply

6 years ago, # ^ |

← Rev. 2 →

In the dp when you consider element x, you make 3 trials. In the jth trial (j ranges from 0 to 2), you try to take the triplet [x, x+1, x+2] j times (if minimum(count(x), count(x+1), count(x+2)) >= j), and you add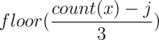 $\text{[math]}$ to the jth trial's result. So basically, what is left from x in the jth trial is just consumed in the form of triplets [x, x, x].

→ Reply

kumaraditya1999

6 years ago, # ^ |

can you explain by writitng the recurrence relation for dp ?

→ Reply

6 years ago, # ^ |

+16

One possible way:

Let dp[i][j][k] be the maximum count of triplets that can be formed if you start at value i, j occurrences of value i and k occurrences of value i + 1 are consumed in the form of triplets [x, x + 1, x + 2] where x < i. And let co[i] be the initial count of value i occurrences.

For 0 ≤ l ≤ 2, if min(co[i] - j - l, co[i + 1] - k - l, co[i + 2] - l) ≥ 0,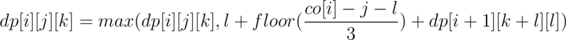 $\text{[math]}$ (where dp[i][j][k] is initially 0). The answer is dp[1][0][0] (Loop order: i = m → i = 1).

→ Reply

coolreshab

6 years ago, # ^ |

Why are you considering l upto 2 why not till min >=0 ?

→ Reply

6 years ago, # ^ |

Read my first two replies to the top level comment.

→ Reply

kumaraditya1999

6 years ago, # ^ |

thanks alot

→ Reply

toughdude123

6 years ago, # ^ |

Sir, why are you adding floor((count(x) — j)/3) to the jth trial?

→ Reply

6 years ago, # ^ |

Because you consumed j occurrences of x in form of triplets [x, x + 1, x + 2]. So you want to consume what is left from x in form of triplets [x, x, x] (and if 2 or 1 occurrences of x are left at the end, you will not use them). This is equivalent to taking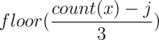 $\text{[math]}$ .

→ Reply

toughdude123

6 years ago, # ^ |

Got it now, thanks !!

→ Reply

MagicSpark

6 years ago, # |

Fast editorial.Great!

→ Reply

ghoshsai5000

6 years ago, # |

← Rev. 2 →

Hi everybody,

In case anybody needs practice with B, AtCoder Beginner Contest 117 had a very similar problem here.

Here is my editorial for Problem C. I believe it is easier to understand than the editorial provided here. Let me know if you have any doubts. :)

Here is my editorial for E.

→ Reply

fuad036

6 years ago, # ^ |

Thanks a lot!! nice explanation

→ Reply

akhilreddy_95

6 years ago, # |

In C, if a=2^x . Then as per "Denote the highest bit of a as x (that is largest number x, such that 2^x≤a) and consider b=(2^x−1)⊕a. It's easy to see that if a≠2^x−1 then 0<b<a holds." b=2^(x+1)-1. which does not hold in between 0 and a.

→ Reply

6 years ago, # ^ |

It's probably a mistake. I think b should be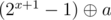 $\text{[math]}$ .

→ Reply

birchtree

6 years ago, # ^ |

Thanks a lot !

→ Reply

birchtree

6 years ago, # ^ |

I was wondering for a long time until I found that it's a mistake

→ Reply

TheNoOne

6 years ago, # |

Has anyone solved "D" using greedy approach? If yes, can you please share!

→ Reply

zhangqingqi

6 years ago, # |

how to dp in AC automaton? how to calculate the answer of all the current suffixes? Could you explain in details. thanks cdkrot

→ Reply

TheScienceGuy

6 years ago, # |

In C, we denote x as 2^x <= a, but then the explanation states the following: "consider the case when a=(2^x)-1". Could someone explain what they exactly mean here?

→ Reply

Akash_123

6 years ago, # ^ |

← Rev. 2 →

It should read "consider the case when a=2^(x+1)-1". I was also confused by that. Basically, a is a string of 1s in binary.

→ Reply

mayank_ag

6 years ago, # |

can someone tall the c++ codes for 2nd and 3rd question, maybe with comments and steps will be more helpful

→ Reply

6 years ago, # |

I think in C editorial, meaning of x should be the smallest number such that 2^x > a.

→ Reply

WaterColor2037

6 years ago, # |

Thanks for the editorial. I didn't realize the editorial was already out, cause I didn't see the "Recent actions" so much. Adding a link to the original announcement blog post ( http://mirror.codeforces.com/blog/entry/65059 ) would be helpful :)

→ Reply

LJB00126

6 years ago, # |

-11

In fact, we can use a simple way to solve the problem C.
Although this way is not very good.

#include<bits/stdc++.h>
using namespace std;
int wyj[25] = {3,7,15,31,63,127,255,511,1023,2047,4095,8191,16383,32767,65535,131071,262143,524287,1048575,2097151,4194303,8388607,16777215,33554431,67108863};
int qwq[25] = {1,1,5,1,21,1,85,73,341,89,1365,1,5461,4681,21845,1,87381,1,349525,299593,1398101,178481,5592405,1082401,22369621};
bool check[67108869];
int ans(int x)
{
    if(x == 1)  return 0;
    if(x == 2)  return 3;
    if(check[x])
    {
        for(int i = 0; i < 25; i++)
            if(wyj[i] == x)
                return qwq[i]; 
    }
    else
        for(int i = 0; i < 25; i++)
            if(x <= wyj[i])
                return wyj[i];
    return -1;
}
int main()
{
    for(int i = 0; i < 25 ; i++)
        check[wyj[i]] = 1;
    int q, tby;
    scanf("%d",&q);
    for(int i = 1; i <= q; i++)
    {
        scanf("%d",&tby);
        printf("%d\n",ans(tby));
    }
    return 0;
}

→ Reply

MotaSanyal

6 years ago, # |

Can anyone explain me the intuition behind the process in problem E ? Its hard to come up with such an idea

→ Reply

Diego1149

6 years ago, # ^ |

This comment and read the editorial to the problem: http://mirror.codeforces.com/blog/entry/65059?#comment-490669

It's not obvious to me how to come up with such idea, it just seems like its a tricky known technique :S

→ Reply

tusharjape007

6 years ago, # |

Please correct me if I'm wrong but it seems that in C the given editorial solution leads to wrong answer. For eg. if a=11 then given solution would give b=12. Instead it should have been b=4 (which we get by complimenting binary rep of a=11, considering significant bits).

→ Reply