Hello everyone!
I would like to invite you to participate in February Circuits '19. It's a long contest that will start on Feb 15, 9:00 PM IST (check you timezone). Contest will run for 9 days.
The problem set consists of 7 traditional algorithmic tasks of various difficulties and 1 approximate problem. For traditional algorithmic tasks, you will receive points for every test case your solution passes — so you can get some points with partial solutions as well. For the approximation task, your score depends on the best solution in the contest so far. Check contest page for more details about in-contest schedule and rules.
I'm the tester and Alpha_Q, aminul, Apptica is the setters. I would like to thank HackerEarth admin panel, without them we do not have such contests. Below is the detail of problem set:
- Day-0: Easy, Easy-medium, Approximate.
- Day-2: Easy-Medium, Medium.
- Day-4: Medium, Medium-hard.
- Day-6: Hard.
As usual, there will be some nice prizes for the top five competitors:
- First place: $100 Amazon gift card + HE t-shirt.
- Second place: $75 Amazon gift card + HE t-shirt.
- Third place: $50 Amazon gift card + HE t-shirt.
- Fourth place: HE t-shirt.
- Fifth place: HE t-shirt.
Hope to see you at the scoreboard! GL & HF.
UPD: Congratulations to the winners
- 1.tourist
- 2.bluedawnstar
- 3.pmnox










The contest will start in 30 minutes!
How to solve cost recovery?
Let pi be the prefix sum of b. Then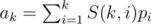 , where S(n, k) is the Stirling number of second kind. You can arrange these in matrix form and to find p, you can multiply vector a with inverse of the matrix of Stirling numbers of second kind, which is surprisingly the matrix of signed Stirling numbers of first kind!
, where S(n, k) is the Stirling number of second kind. You can arrange these in matrix form and to find p, you can multiply vector a with inverse of the matrix of Stirling numbers of second kind, which is surprisingly the matrix of signed Stirling numbers of first kind!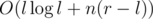
Since you only need to find bl... r, you need to find pl - 1... r. You can find the (l - 1)th row of signed Stirling numbers of first kind with FFT and then transition to next rows in linear time. Since r - l < 100, you'll do this only r - l times. This solution works in
Got it, thanks!
No idea why you got so many downvotes :/