Here is the editorial for the round. The comments for this post also have lots of great explanations of alternative solutions, make sure to check them out!
I hope you've enjoyed the contest!
Here is the editorial for the round. The comments for this post also have lots of great explanations of alternative solutions, make sure to check them out!
I hope you've enjoyed the contest!
| Название |
|---|


I took my time and sometimes made more complicated solutions than necessary, but at least I found a bug: this gives null pointer exception. Apparently, indirection through different operations is a problem.
A2: Can be done without extra qubits (obviously), but the implementation is more difficult. I chose up to 3 pivot indices, used an operation from Canon to prepare the right state on them (because why bother, it's fast enough) and then just ran the controlled X gate appropriately to change the qubits with the remaining indices.
D6: Pretty simple actually. I made an operation that only modifies states encoding a and a + 1 in binary representation (for any a < 2N - 1): it sends something like 0.9 of the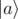 state to
state to 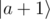 and 0.9 of the
and 0.9 of the 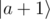 state to
state to 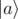 . Then, I ran this operation 2N - 1 times, on each possible a in decreasing order. When it gets a state
. Then, I ran this operation 2N - 1 times, on each possible a in decreasing order. When it gets a state 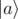 on the input, it sends 0.9 of it to
on the input, it sends 0.9 of it to 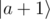 , keeps (0.1)^2 in
, keeps (0.1)^2 in 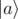 and distributes the rest in
and distributes the rest in  , ...,
, ..., 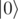 .
.
C3: I made a kind of finite state machine — a function that computes the remainder mod 3 gradually and recursively calls itself with the current value of the remainder and unprocessed qubits. It always cuts off 3 qubits, packs their remainder into one and uses it as the control qubit for itself.
I though about finishing it with B2 — I figured out that I need to use 1 extra qubit and send everything to states such that each of the 4 Z-basis vectors doesn't appear somewhere, but I didn't figure out easily how to do that and at this point, what difference does it make.
Why 0.9 instead of half and half?
I tried the same thing but got TLE. I think this is the biggest lesson of the contest — IncrementLE is horribly slow! If I just wrote my own, I would've solved certain problems a lot faster. Same thing happened on the mod3 problem.
Keep in mind that the amplitude of smaller states in the result decreases exponentially — if you send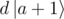 to
to 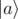 , then d of that to
, then d of that to 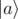 to
to  , you actually sent
, you actually sent 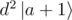 to
to  . It's just safer to pick a larger d so it wouldn't drop too much.
. It's just safer to pick a larger d so it wouldn't drop too much.
Thanks for the contest! I enjoyed learning about Quantum Computing (or did I, it's a superposition). Every time I felt finally I understand, just two seconds later I reset to the is this legal? basis state.
BTW, for someone interested in a career related to Quantum Computing, Does anyone know the options and the prerequisites?
"Every time I felt finally I understand, just two seconds later I reset to the is this legal? basis state."
You're too focused on measuring your progress.
Maybe that why my understanding usually collapse!
I think my confusion stems from the common explanation using electrons, spinning, waves and alike especially in folk science videos, and I lack background in physics (heck, I got F in my last Physics course). I find the vectors and matrices interpretations more intuitive. It's perhaps the same reason that a developer doesn't have to learn about charges and electricity to be able to code!
Spoiler alert: in physics, it's the "vectors and matrices interpretation" that's used to compute everything. If you tried a more classical-physics approach, you run into trouble already with seemingly simple things like scattering of an electron on an atom. You can use physical intuition to check if the calculations you're doing make sense in some special cases, but otherwise, you need pure math if you don't want to end up making wild guesses.
My solution to B2 (In the editorial this is marked as TODO) (This might have some wrong minuses):
The way I figured this out was by starting at the bottom (We somehow want 3 elementary states where each possible state is the sum of two of them). The angles are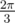 , so we should be able find a unitary (hence angle preserving) operation that maps the initial states to them. By using controlled operations, we can keep the first state at |00⟩, so we can focus on the second state (and the third one will be automatically correct). Then reconstruct the operation from bottom to top.
, so we should be able find a unitary (hence angle preserving) operation that maps the initial states to them. By using controlled operations, we can keep the first state at |00⟩, so we can focus on the second state (and the third one will be automatically correct). Then reconstruct the operation from bottom to top.
That was almost exactly what I came up with. I'm glad I stayed up all night to figure it out!
Thanks for the contest! The difficulty was perfect I think. It wasn't a speed race, but still all problems were solvable.
A couple of my solutions if they are different than editorial (or editorial doesn't exist) and some comments:
A2: Took me much longer than it should have. I didn't think of the uncomputing trick. I came up with many very messy ideas, but finally passed using a similar thing as A1: construct the solution bit by bit and when the next bit would split a state into two, rotate by appropriate angle.
B2: Initially I thought to add a qubit, then make some operations so that one of the states is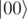 and other two are
and other two are 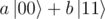 and then measure and proceed only if I see
and then measure and proceed only if I see 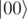 , but it left me with non-orthogonal qubits. Later, I found online many resources telling the theoretical base for this (generalized measurement) but they didn't describe how to construct the system. Finally when I managed to do it, I also understood why the initial thing happened: I made sure that the two
, but it left me with non-orthogonal qubits. Later, I found online many resources telling the theoretical base for this (generalized measurement) but they didn't describe how to construct the system. Finally when I managed to do it, I also understood why the initial thing happened: I made sure that the two 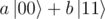 states have |a1| = |a2| but if a1 ≠ a2 (because they have different complex phase), they carry some part of the information, which gets destroyed at measurement.
states have |a1| = |a2| but if a1 ≠ a2 (because they have different complex phase), they carry some part of the information, which gets destroyed at measurement.
C3: I iterated over all bitmasks with 0,3,6,9 bits. I wanted to use ControlledOnInt but it timed out. But an equivalent of this solution is to flip bits accordingly, such that at the moment of measurement I have n ones iff the qubits were initially in the bitmask state. This passes the time limit.
D5: Googling Hessenberg matrix gave me this page. It says that a unitary Hessenberg matrix is a product of matrices where there is one 2x2 rotation and the rest is diagonal. So the algorithm is to repeat: shift the matrix up by 1, Hadamard gate on top left corner. Here comes the problem that IntegerIncrementLE is very slow, but increment by 1 is rather easy to implement.
I found a possible bug in Q# (or is it expected behavior?): when running multiple test cases on the same instance of the simulator, the newly created qubits are not in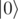 state, but rather in
state, but rather in 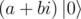 , probably dependent on the previous computation, but I didn't check it.
, probably dependent on the previous computation, but I didn't check it.
As far as I know,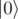 and
and 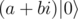 — it's the same qubit. proof
— it's the same qubit. proof
Technically, yes. I don't see much of a proof under this link (other than just stating it) but it's easy to prove mathematically if you calculate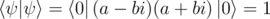 . But in terms of preparing a qubit in exactly a given state (like the ones I need to distinguish in task B), it becomes a problem.
. But in terms of preparing a qubit in exactly a given state (like the ones I need to distinguish in task B), it becomes a problem.
True — sometimes it does matter though, which confused me for a while.
This is the reason why R1 and Rz are different, and also why you can rotate with respect to PauliI — global phase matters sometimes, when you use controlled gates.
That's the difference between global and relative phase. Global phase doesn't matter, but as soon as you have a superposition where you only apply the phase to some terms and not others, you apply a relative phase between the one to which you do and the ones to which you don't, which does matter.
I loved the round and the editorial. Also, I thought I could share some of my solutions that are interestingly different.
C3. Instead of summing mod 3 I created 4 1-qubit states — first 3 represented subsequent reminders mod 3 and the last one was just to prevent multiple token movement.
Firstly, I set up this state to 1000 — starting reminder is 0. Qubit with value of 1 is called a token and will "move around" the state.
Now I create controllable operation MoveToken:
And apply it controllably for each input qubit. It can be seen that state 1000 changes to 0100, 0100 to 0010 and 0010 to 1000.
Finally, just CNOT(0, y). Solution.
D3. My logic in this task was as follows:
This looks like a sum of tensor products of n times I and X (I being the first diagonal, X being the second).
I cannot add those two matrices with qubits, only multiplication of matrices is allowed;
But exp funcion has this property of changing addition into multiplication;
So just compute exp(i theta [PauliI * n]) and then exp(i theta [PauliX * n]) for some nontrivial theta. I used theta = 0.4, but I guess almost all thetas are good thetas.
This solution got accepted but I am actually not sure if that logic wasn't faulty.
Solution. Sorry, I can't into arrays
D4. I reused D3, but with permuting input qubits so that they fit into correct columns.
Some of mine solutions:
A2: I've ended up with a more general solution. Split the set of vectors that we need to superpose (given by bit arrays) into two groups based on the value of the first qubit (continue to the next qubit if all vectors lay in one group). Now try to generate state a|0⟩|GR0⟩ + b|1⟩|GR1⟩ from |0..00>. Since groups can have different sizes (for example, 1 and 3 if 4 vectors are given) apply appropriate rotation to the first |0> qubit to obtain a|0⟩ + b|1⟩ (i.e. sqrt(1/4)*|0> + sqrt(3/4)*|1> in case of the group sizes 1 and 3). Generate both groups recursively but apply them controlled by first qubit.
C3: You just need to implement "add 1 mod 3" subroutine on the ancilla qubits. For some reason library function
ModularIncrementLEgave me TLE.D6: Note, that add1 operation looks like first subdiagonal (with 1's) and top right 1. Now you just need to merge this subdiagonal with top right element. I've ended up implementing general two-level unitary subroutine for this, though I think there should be simpler way.
B2: Ah, the trickiest one. Consider the orthogonal vectors
v0 = |10> + |00> + |01>
v1 = |10> + w|00> + w^2|01>
v2 = |10> + w^2|00> + w|01>
This is actually a Fourier transform (DFT3) on 3 vectors |10>, |00>, |01>.
Notice, that
v0 — v1 = (1-w) ( |00> — w^2|01> ), which is collinear to |0> x Z(C) and orthogonal to v2
v1 — v2 = (w-w^2)( |00> — |01> ), which is collinear to |0> x Z(A) and orthogonal to v0
v2 — v0 = (w^2-1)( |00> — w|01> ), which is collinear to |0> x Z(B) and orthogonal to v1
Hence,
|0> x Z(C) orthogonal to v2
|0> x Z(A) orthogonal to v0
|0> x Z(B) orthogonal to v1
So, the solution is to apply adjoint of the Fourier transform (on vectors |10>,|00>,|01>) to the state |0>Z(q) (where q is given) and distinguish vectors |10>, |00>, |01> by measurement. If it's |10>, then q can't be A, coz AdjointDFT3(|0> x Z(A)) and |10> are also orthogonal (since orthogonality is preserved under unitary operations). Similarly for other states.
The actual generation of DFT3 for me was pain in the ass, but I finally managed it :)
Wow, the FT approach is really nice!
Nice to see that someone else found the DFT approach too. I actually first did B1 with such a transform, and then realized I could utilize all my hard work in factoring the 3x3 DFT (took me like 5 hours) in B2.
My solution to B2:
Design a 2-bits operation U s.t.
So there is no in
in  , no
, no 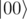 in
in 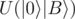 , and no
, and no 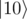 in
in 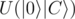 .
.
Just apply U and measure.
I got such U in 2 steps.
Step 1, same as someone used in A1.
Step 2, design some U2 s.t.
consider new basis
now it becomes
to get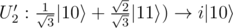 we need controled-Ry and controlled-Rz (quite similar as before, just remember to controll so that it will not change
we need controled-Ry and controlled-Rz (quite similar as before, just remember to controll so that it will not change 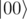 and
and 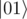 , and add controlled-Rz( - π) to change phase on
, and add controlled-Rz( - π) to change phase on 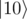 )
)
to change basis and change back, use controlled-H (
(ControlledOnInt(0,H)) ([qs[1]],qs[0]);)now we get U2
everything is done.
(btw, can anyone teach me how to use bra-ket notation in latex on codeforces? it seems there's no {braket} package)This would do the work.
Thanks!
I found unitary decomposition (Decompose a unitary matrix to several rotations) is really useful. It makes solving A1 B1 B2 trivial (although quite slow...). You just need to find an appropriate unitary matrix that solves the problem.
For D* problems, If you implement a gate that could swap 2 states, them some of them become really easy. For example, to solve D4 you just need to swap some rows and columns of D3, and D5 is basically D2.
Yes, (controlled-)X means swap 2 cows, and (controlled-)H means "mix" 2 cows. I don't realize it until D6.