Во первых, расположим все вершины так, чтобы слева направо их высоты убывали.

Теперь важный факт — как бы мы не расставляли подъёмники, в любом случае нам придётся поехать из последней вершины в первую, возможно с помощью нескольких подъёмников.
Заметим, что если мы разделим путь из последней вершины в первую на два, остановившись где-то, то тогда мы сможем забрать всех людей с какой-то дополнительной вершины.
Если мы сделаем такие остановки во всех вершинах между первой и последней, то у нас уже будет хороший ответ и мы сможем добраться из любой вершины в любую другую.

Теперь подумаем, а какие остановки нам реально нужны. Немного порисовав на бумажке становится понятно, что остановки нужны во всех вершинах, в которые не входит ни одно ребро (кроме первой вершины). Это так, потому что мы не сможем попасть в неё из первой вершины. Также нам нужны подъёмники из всех вершин, из которых не выходит ни одно ребро, потому что надо же как-то оттуда выбираться.
Если мы сделаем такой маршрут, который идёт от последней вершины к первой, по пути собирая все вершины, описанные выше, мы и получим оптимальный ответ.

Будем строить две выпуклые оболочки по левым и правым границам ворот так, что бы они всегда начинались из одной точки. Начнём из точки (0; 0) и будем рассматривать ворота в порядке увеличения координаты Y. Пусть при добавлении ворот 1, 2 и 3 проблем не возникает и тогда мы переходим к следующим. А при добавлении ворот 4 оболочки пересекаются.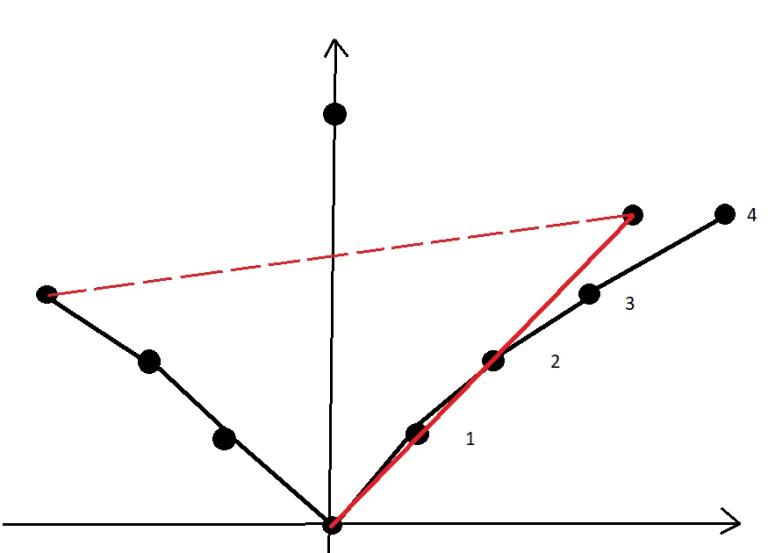 Заметим, что левая оболочка теперь не является корректным путём, так как не проходит через все ворота. Её можно очистить. В качестве новой стартовой точки будем рассматривать все точки в правой оболочке начиная с первой. Если при текущей точке оболочки продолжают пересекаться, то удаляем эту точку, а к ответу прибавляем расстояние до следующей. 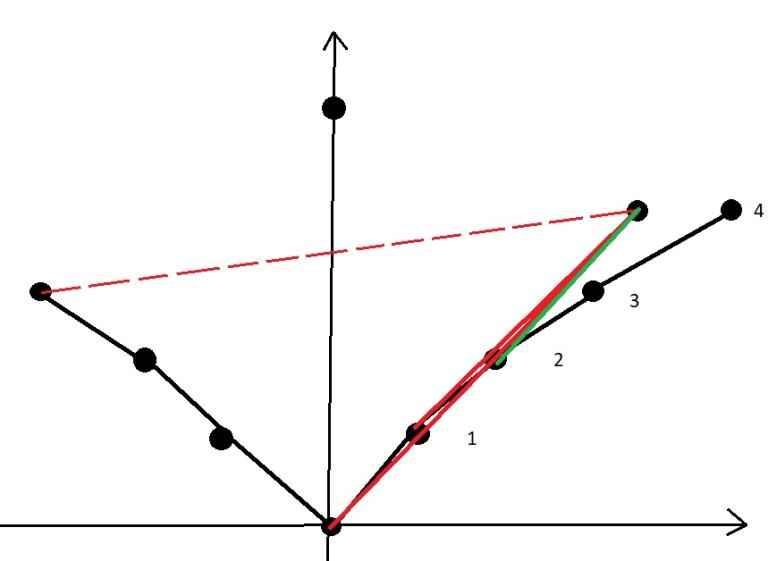Таким образом, новой стартовой точкой будет правая граница вторых ворот, а к ответу будет прибавлено расстояние между точками (0, 0) и правой границей первых ворот и расстояние между правыми границами ворот 1 и 2. Все ворота будем рассматривать подобным образом и в конце рассмотрим ворота, состоящие из точки (0, Q). После этого в оболочках останутся две точки, расстояние между которыми нужно прибавить к ответу (в обоих оболочках это будут одни и те же точки).

Для решения задачи остаётся разобраться ещё с парой вопросов. Как определить, какая оболочка корректна, а какая нет: размер корректной оболочки всегда больше (очевидно, если немного порисовать). Как определить, что оболочки пересекаются: рассмотрим два вектора, которые образуют две первые точки в каждой оболочке. В нормальной ситуации вектор из правой оболочки должен быть повёрнут относительно вектора из левой по часовой стрелке, иначе оболочки пересекаются (для того чтобы проверить это, достаточно посмотреть на знак векторного произведения этих векторов). Время работы линейное. Вроде всё.

Алгоритм правильный, но только во втором пункте может быть проблема. Как именно Вы проверяли каждую соседнюю пару на правильность?

Планируется ли добавление личного турнира в тренировки?

У меня трёхмерная дп N * M * 5.

dp[x][y][i] — кол-во способов разместить i колец при условии, что i-ое кольцо будет иметь координату {x, y}