Блог пользователя computerbox

Croatian Open Competition in Informatics (COCI) Round 6 Discussion
Автор computerbox, история, 6 лет назад, По-английски

Hi ! Let's discuss Croatian Open Competition in Informatics (COCI) Round 6 here . http://hsin.hr/coci/.

How to solve problem Sličice (Dynamic Programming or Greedy ) and Simfonija (Segment Tree ) ?

  • Проголосовать: нравится
  • +8
  • Проголосовать: не нравится

»
6 лет назад, # |
  Проголосовать: нравится +8 Проголосовать: не нравится
Sličice
→ Ответить
»
6 лет назад, # |
← Rev. 2   Проголосовать: нравится +5 Проголосовать: не нравится

For Simfonija, notice that the n - k smallest values of |(Ai + X) - Bi| will always be a contiguous subarray of the sorted Ai - Bi array. As X increases, that subarray moves from the highest Ai - Bi to the lowest. So simply loop over all values of X, move the subarray boundaries if necessary and calculate the sum using prefix sums.

→ Ответить
»
6 лет назад, # |
  Проголосовать: нравится +14 Проголосовать: не нравится

You can solve all problems here: https://oj.uz/problems/source/374

→ Ответить
»
6 лет назад, # |
  Проголосовать: нравится +5 Проголосовать: не нравится

I would like to know the solution to task E(Mobitel).

Any help would be much appreciated.

→ Ответить
  • »
    »
    6 лет назад, # ^ |
      Проголосовать: нравится +13 Проголосовать: не нравится

    The dynamic programming solution O(RSN) is straight-forward, the states are:

    For each cell and each n <= N-1, how many path exist that finish in this cell whose product is exactly n).

    The trick is to change the states to:

    For each cell and each k, how many paths exist that finish in this cell and such that k is the largest integer number we can multiply in the remaining part of the path without reaching N?

    Instead of keeping the value of the product until the current cell, we keep how much the product can be from here to the end. The crucial difference is that the only interesting values of k are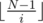 for 1 ≤ i ≤ N (prove it). Hence the solution is .

    → Ответить
»
6 лет назад, # |
  Проголосовать: нравится 0 Проголосовать: не нравится

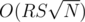My this code takes runtime error in mobitel please help me. https://paste.ubuntu.com/p/txXDR6G8wG/

→ Ответить