Привет!
Мы поддержали отображение LaTeX-формул с помощью MathJax в новых постах и комментариях. Теперь формулы будут такие же красивые, как и в условиях задач. Из минусов — они не сразу отображаются, а переотрисовываются после отображения страницы. Старые посты и комментарии отображаются по старому (уже много старого контента, обратная совместимость очень важна). Замечу, что если вы отредактируете старый пост, то всё равно он будет отображаться в старом стиле.
Несколько примеров: $$$1 \le n \le 10^{12}$$$, $$$c = \sqrt{a^2+b^2}$$$, $$$i\hbar\frac{\partial}{\partial t}\left|\Psi(t)\right>=H\left|\Psi(t)\right>$$$.











Can you write something here to see how it looks like?
I understand. It need like this. yor need use double dollar sign to include your code
Thanks a lot.
You have to use $ or $$ like in LateX
$a^2$
$$$a^2$$$
$$a^2$$
Sound matrix multiplications am I right? :D
Maybe Sound signal can use the function too? I use the Gamma Matrix to calculate the loss function with higher CNN-layer similarity in Picture Style Transfer.
Whoa, slow down senpai, I need a few more time to be familiar with ML models. :D
Ah nice
The old style: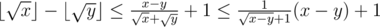
The new one: $$$\lfloor \sqrt{x} \rfloor - \lfloor \sqrt{y} \rfloor \le \frac{x-y}{\sqrt{x}+\sqrt{y}} + 1 \le \frac{1}{\sqrt{x-y}+1}(x-y) + 1$$$
Looks so much better!
much more pretty right :D
Good job!
Good job
It seems there is an error on displaying when I change the revision of comment to see. Check the revision 1 and move back to revision 2 of my comment then you will see the bug. MikeMirzayanov
$$$\mathbb{CODEFORCES}$$$
nice
What was the LaTeX renderer before? I always thought it was some kind of Russian bootleg MathJax.
Looks very pretty :)
$$$ \huge \mathcal{O}( N ) $$$
Testing
If $$$f(x)=\frac{1}{1-x^k}$$$, then $$$g(x)=(\ln f)(x)=\sum_{i=1}^{\infty}\frac{1}{i}x^{ik}$$$. Proof:
I think, that you forgot to try
\left(instead(and\right)instead). This allows to auto detect correct height of parentheses under summation, like this:Yeah, you're right. But sometimes it's too complicated.
Can explain me why backward compatibility is very important?
Deleted and screw uplaoding a photo
Proof left as an exercise to the reader.
I have already proved this B).
hello, my platinum blue men
nchn orz
$$$a^2$$$
$$$ы^2$$$
Nice, Now I can draw beautiful owls in my posts. Thanks Mike!
LOL
$$$\require{AMScd}$$$ \begin{CD} T @>h>> A\\ @. @VV n V\\ M @<<s< K\\ @VV iV @.\\ K @>>e> !\\ \end{CD}
red coder maths r very strong
Let $$$T=kd$$$,
Why the
\sumbecame\prod?....Maybe you can use..
\Sigma_{i=1}^n \Sigma_{j=1}^m d_1(\gcd(i, j))It seems that it was fixed now, also thank you...
I'm just crack a joke,if you use the \Sigma,it will be too small...
It is not always true when $$$n<\varphi(m)$$$. For example, $$$6^{2}\not\equiv 6^{4+2}\pmod8$$$.
It's true for $$$n>\log_2 m$$$
More accurately, it's true for $$$n\ge\max_{i=1}^k\alpha_i$$$, where $$$m=p_1^{\alpha_1}p_2^{\alpha_2}\cdots p_k^{\alpha_k}$$$.
what's the theory behind the fomula plz
Let $$$m=p_1^{d_1} \dots p_n^{d_n}$$$. Consider the periodicity of $$$a^n$$$ on each $$$p_k^{d_k}$$$ separately. By Chinese Remainder Theorem, pre-period of $$$a^n$$$ modulo $$$m$$$ will be equal to the maximum of pre-periods modulo $$$p_k^{d_k}$$$ and period itself will be least common multiple of periods modulo $$$p_k^{d_k}$$$.
On each $$$p_k^{d_k}$$$ pre-period will be either $$$0$$$ if $$$\gcd(a,p)=1$$$ or at most $$$d_k \leq \log_2 m$$$ otherwise. And period will always be the divisor of $$$\varphi(p_k^{d_k})$$$ which is in turn the divisor of $$$\varphi(m)$$$. Thus their least common multiple will be the divisor of $$$\varphi(m)$$$. This gives you the result above, given that $$$\varphi(m) \geq \log_2 m$$$.
thank you vvery much. seems that I have a lot of things to catch up with
I don't care. I want another codeforces round asap.
You can have hundreds of virtual contests.
WoW, it's cool! Thank you~
It was finally realized. A question about using LaTeX in blogs
The most convenient thing is that you can copy the formula by $$$\text{Right Click}\rightarrow\text{Show Math As}\rightarrow\text{TeX Commands}$$$.
WAIT! Why all
\sums became\prods? $$$\underset{\text{actually \sum}}{\underline{\sum}}\neq\underset{\text{real \prod}}{\underline{\prod}}$$$Fixed!
Looks like I found the following feature: If you use
\newcommandor\renewcommand, it will affect all comments below yours. Apologies to all the people between my two comments that got confused by this.Stackexchange had the same issue, but there some people could at least edit the answers/comments and remove the malicious code. Their fix (mentioned in an answer to the linked post) was to wrap posts in
\begingroupand\endgroup. Another fix mentioned there was to use\resetstack. MikeMirzayanov could you look into that?Edit: It looks like
\newcommandand\renewcommandnow get stripped from mathjax parts of comments. This should deal with people replacing $$$\pi$$$ with 40 owls for now. Nevertheless, I would love to see support for a\newcommandwhose scope is just the comment it was written in. (But I see that implementing and testing that might take some time.)It is a great joy to solve mathematical problems using $$$LaTeX$$$ !
this is disgusting, genuinely
More generally, $$$F_n \equiv 0 \mod F_m$$$ if $$$n \equiv 0 \mod m$$$.
Is this fomula true? What's this theroem called?
\begin{equation*} e^{\pi i} + 1 = 0 \end{equation*}
Well, Let's see some tables
Testing
Testing a second time
Yep, dacin21's feature is still not fixed.
Wow, I find a person use the same picture as me! orz.
$$$-\dfrac{\hslash^2}{2m} \, \dfrac{\mathrm{d}^2 \psi}{\mathrm{d} x^2}$$$
$$$-\dfrac{\hslash^2}{2m} \, \dfrac{\mathrm{d}^2 \psi}{\mathrm{d} x^2}$$$
Oh boi we should forbid posting Hamiltonians on codeforces...
strange suggestion, coming from a string theorist...
and what does this have to do on a programming website? this website is for competitive programming, not math.
Relax competitive programming is just maths + coding
do you realise what you're saying? just because some random website called codeforces decides to mess around with us by giving us terrible, useless problems full of math doesn't mean the whole thing called COMPETITIVE PROGRAMMING is like this.
read before you comment because people who don't know better will take what you say as being true.
\begin{CD} Me\\ @VV V\\ @>>> \\ solving\ problems @VVV @.\\ @<<< \\ @VVV\\ playing\ with\ LaTeX \end{CD}
$$$\LaTeX$$$
It's fantastic! $$$f(x)=g(y)+1$$$
Great!It will make codeforces better. :D
$$$\frac{-b\pm\sqrt{b^2-4ac}}{2a}$$$
That's what you love :D AhmadLoiy
$a
Is it rated ?
Does it support
MarkdownandMathJaxin the same post/comment ?Here I'm trying to test both of this:
Markdown & Latex Example
Codeforcesis awesome!! Now let's try to write amatrix:Inline$$$\begin{bmatrix}a & b\ c & d\ e & f \end{bmatrix}$$$ andNow in
new linematrix:`Seems it doesn't work in
inlineform.Use $$$\begin{bmatrix}a&b\\c&d\\e&f\end{bmatrix}$$$, I succeeded.
Great!
(2 + 3) / 55
new LaTex looks much better
<p>Unable to parse markup [type=CF_MATHJAX]
F(n)f(n)=∑d∣nf(d)=∑d∣nF(d)μ(nd)
umm…… seem to be unable to use LaTex on my computer……
It's so cool, I want to comment too :
Am I the only one who feels that it doesn't work now?
Inline: $$$\frac{x}{y}\in\mathbb{R}$$$
Block:
Displaystyle:
UPD: never mind, I've changed my browser recently, and now I seem to have to change my mathjax math renderer. Sorry for necroposting