Для нахожения ответа переберем все возможные рестораны, в которых могли пообедать три Кролика. Посчитаем ответ для каждого ресторана. Из всех ответов выберем максимальный. Ответ для ресторана i считается по формуле, описанной в условии. Сложность решения O(N).
Посчитаем количество букв, которые встречаются в строке s нечетное количество раз. Пусть это количество равно k.
Заметим, что если k = 0, то первый игрок сразу же побеждает — он легко может составить палиндром, поставив одинаковые буквы в разные концы строки (так как общее количество всех букв четное, он сможет это сделать).
В случае k = 1 первый игрок опять-таки сразу же побеждает — сначала он строит палиндром из букв, которые встречаются четное количество раз, а потом вставляет в середину полученной строки те символы, количество вхождений которых в строку s нечетно. Утверждается, при k > 1 задача имеет следующее решение: если k четное – победил второй игрок, иначе победил первый игрок.
Докажем это утверждение. Пусть k = 2. Первый игрок своим ходом может сделать ходы двух типов. Ход первого типа состоит в том, чтобы уменьшить k до 1, удалив одно вхождение буквы, которая встречалась нечетное количество раз. Однако такой ход ведет к поражению, ведь после него второй игрок может составить палиндром.
Ход второго типа состоит в том, чтобы удалить букву, которая встречается четное количество раз, таким образом увеличив k до 3. В таком случае, второй игрок может ответить аналогичным ходом, удалив такую же букву. Так как количество ходов этого типа конечно, то рано или поздно первый игрок вынужден будет сделать ход первого типа, а значит — перейти в проигрышную для себя позицию.
В случае k = 3 первый игрок первым же ходом может уменьшить k до 2, убрав букву, встречающуюся нечетное количество раз. Если второй игрок попробует увеличить k до 3, то первый игрок аналогичным ходом сможет опять уменьшить k до 2. Легко увидеть, что последним в этой цепочке ходов будет ход первого игрока, а значит – он переводит игру в состояние с k = 2, которое является выигрышным для него и проигрышным для его соперника. Аналогичными размышлениями, применяя математическую индукцию, утверждение доказывается для произвольного k.
Получается достаточно простое решение за О(|S|)
C. Девочка и максимальная сумма
Для каждой ячейки массива посчитаем количество запросов, которые ее покрывают. Утверждается, что ячейке, которую покрывает большее количество запросов, нужно ставить в соответствие большее число. Более формально: пусть b — массив, в i-ой ячейке которого записано количество запросов, покрывающих эту ячейку, а – входной массив. Отсортируем эти массивы. Утверждается, что ответ в таком случае равен 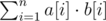
Докажем это утверждение. Рассмотрим какие-то индексы i < j, а так же соответсвующие им элементы a[i], a[j] , b[i], b[j] (a[i] ≤ a[j], b[i] ≤ b[j]). Эти элементы вносят в ответ следующую величину: a[i]·b[i] + a[j]·b[j]. Поменяем элементы a[i] и a$[j]$ местами. Теперь эти элементы вносят в ответ величину a[i]·b[j] + a[j]·b[i]. Рассмотрим разницу между полученными значениями:
a[i]·b[j] + a[j]·b[i] - a[i]·b[i] - a[j]·b[j] = b[j]·(a[i] - a[j]) + b[i]·(a[j] - a[i]) = (b[j] - b[i])·(a[i] - a[j]) ≤ 0.
Таким образом, перестановка двух любых элементов приводит к неувеличению суммарного результата, а значит — начальный порядок является оптимальным.
Теперь нам нужно быстро научиться считать массив b.
Для этого можно использовать разные структуры данных, поддерживающие модификацию на отрезке (дерево отрезков, декартово дерево и т.д). Однако, существует гораздо более простой метод.
Создадим некоторый массив d. При поступлении запроса li, ri увеличим элементы массива d[li] на 1, и уменьшим значение элемента d[ri + 1] на 1. Таким хитрым образом мы добавляем 1 всем ячейкам от li до ri включительно. После этого необходимо пробежаться по массиву d, накапливая соответствующий результат для b[i].
Теперь, зная массив b, можно легко узнать ответ. Сложность авторского решения — O(NlogN + Q)
Честно говоря, удивлен тем, что с задачей справилось так много участников. Я предполагал решение использующее динамическое программирование, его и опишу.
Для начала, переведем числа L и R в двоичную систему счисления. Теперь заведем такую динамику: d[p][fl1][fr1][fl2][fr2], где p – текущая позиция в двоичной записи чисел a и b (от 0 до количества бит в числе R), fl (от 0 до 1) — переменная, показывающая, что набранное число а строго больше L, fr1 (от 0 до 1) — переменная, показывающая, что набранное число а строго меньше R, fl2, fr2 — переменные, означающие аналогичное значение для числа b.
Напишем динамику в виде рекурсии с запоминанием.
Определим базу рекурсии. Если мы рассмотрели все биты — просто вернем 0.
Определим рекурсивный переход. Узнаем, какой бит может стоять у числа а на позиции p. Мы можем поставить там 0 при одном из двух условий: или у числа L на этой позиции стоит 0, или у числа L на этой позиции стоит 1, а переменная fl1 показывает, что когда-то был выбран бит, который больше соответствующего бита в числе L. Аналогично, мы можем использовать там 1 при одном из двух условий: или у числа R на этой позиции стоит 1, или у числа R на этой позиции стоит 0, а переменная fr1 показывает, что когда-то был выбран бит, который меньше соответствующего бита в числе R. Аналогично, можно узнать, какие биты мы можем ставить в число b. Переберем все возможные варианты расстановки бит, и если результат операции xor в этом бите равен 1, то добавим к ответу для данной расстановки соответствующую степень двойки. Так же необходимо аккуратно пересчитать значения переменных fl1, fr1, fl2, fr2. Среди всех возможных вариантов расстановки надо выбрать максимум.
Запускать рекурсию необходимо от параметров (P,0,0,0,0), где P — количество бит в числе R.
Надеюсь, мой код прояснит все непонятные моменты.
Стоит так же заметить, что подобный подход является в некотором смысле универсальнм и может быть применен для многих похожих задач, например, для вот этой
Сложность алгоритма O(logR)
Благодря комментариям я узнал еще одно замечательное решение, которое тоже решил включить в разбор.
Отдельно рассмотрим случай, когда L = R. Ответ в таком случае, очевидно, равен 0.
Теперь пускай L ≠ R. Пусть Ri — i-ый бит числа R, Li — i-ый бит числа L. Пускай p — наибольшее число такое, что Rp ≠ Lp (индексируем p c 0). Рассмотрим произвольное число в отрезке [L;R]. Легко видеть, что биты, старшие чем бит с индексом p у всех этих чисел одинаковы. А значит, как бы мы не выбирали числа a и b, эти биты ничего не внесут в ответ, ведь их xor равен 0.
Теперь давайте построим числа a и b таким образом:
1) Число a — биты, старшие чем бит с индексом p совпадают с битами числа L, p-ый бит равен 0, остальные биты равны 1.
2) Число b — биты, старшие чем бит с индексом p совпадают с битами числа L, p-ый бит равен 1, остальные биты равны 0.
Легко увидеть, что оба эти числа лежат в промежутке [L;R], а также что их xor превращает в 1 все двоичные розряды, не старшие чем p-ый, то есть ответ при таком выборе максимизируется, и равен 2p + 1 - 1
Сложность алгоритма O(logR)
Решение на Java от AlexanderBolshakov
Если подбирать значение p бинарным поиском, то можно улучшить время работы алгоритма до O(log(logR)), однако на контесте этого делать, естественно, не требовалось.
E. Девочка и задача про дерево
Заметим, что наше дерево – это совокупность некоторых цепочек, начинающихся в корне.
Для начала при помощи поиска в глубину разобьем наше дерево на цепочки. Для каждой вершины узнаем ее глубину, а также номер дерева, в которому она принадлежит. Заведем для каждой цепочки некоторую структуру данных, которая умеет быстро изменять элемент, а также быстро находить сумму на некотором отрезке. Для этих целей, например, идеально подходит дерево Фенвика. Также заведем дерево Фенвика для запросов, затрагивающих корень. Дерево, заведенное для корня в некотором смысле является глобальным — значения, которые в нем присутствуют, актуальны для всех цепочек.
Теперь вспомним задачу С. Там для модификации на отрезке мы использовали массив d, в котором обрабатывали все запросы. Узнавать значения b[i] в той задаче нужно было после поступления всех запросов. Здесь же запросы изменения и запросы на вывод значения, записанного в вершине, выполняются в некотором смысле онлайн. Именно поэтому стоит использовать дерево Фенвика — оно позволяет за cложность O(logN) изменять элемент, и за такую же сложность находить сумму на некотором отрезке. Научимся с помощью дерева Фенвика обрабатывать запросы на добавление на отрезке массива, а так же на нахождение элемента массива. Как уже говорилось, наше дерево умеет выполнять два типа операций:
add(x, y) — добавляет элементу с индексом x значение y
find(x) – находит значение суммы на отрезке от 1 до x
Предположим что поступил запрос на добавление на отрезке l до r значения val.
Тогда просто выполним операции add(l, val) и add(r + 1, - val).
Пусть поступил запрос на нахождения значения элемента с индексом v.
Тогда выполним операцию find(v).
Теперь мы можем вернуться к изначальной задаче.
При обработке запроса типа 0 посмотрим, затронет ли он корень. Если запрос затрагивает корень — следует аккуратно обработать запрос в нашей цепочке, а также сделать соответствующие изменения в дереве Фенвика для корня. Иначе просто обрабатываем запрос в цепочке.
При обработке запроса типа 1 просто найдем соответсвующие суммы в дереве Фенвика для корня, а так же в дереве Фенвика для соответствующей цепочки и просуммируем их.
Сложность полученного алгоритма — O(N + QlogN)
На этом все. Вопросы в комментариях очень приветсвуются.











Я был неправ
Нет. Мы дважды сортируем массив размером N — сначала входящий, а потом массив b
Да, не совсем просто понял Ваше решение.
На самом деле я тоже не совсем прав, ведь q запросов нужно считать и обработать. Сейчас внесу соответствующие изменения.
Можете объяснить поподробнее?
p.s. У меня код не открывается(редирект на анонс).
Давайте попробуем разобраться на примере.
Пусть n=4
Допустим нам нужно обработать такой запрос
1 2
Изначально в массиве d выглядит так: {0,0,0,0}
После первого запроса массив будет выглядет так {0,1,0,-1}
Чтобы узнать b[i], нам просто нужно узнать сумму всех элементов от 0 до i в массиве d Таким образом, b[0]=0,b[1]=1,b[2]=1,b[3]=0;
То есть, когда мы добавляем в d[l] 1, мы говорим, что всем b с индексами от l и до конца мы должны добавить 1. Но это не совсем правда: начиная с 3 элемента мы это делать не должны. Именно потому мы должны добавить в 3 элемент -1.
Советую понять эту фишку, она много где используется, в том числе и для упрощения жизни в задаче Е :)
Вы уверены, что ссылка на код на С++ для D правильная?
Ссылка правильная, просто автор отправлял решения в "админку", а такие решения недоступны для просмотра обычными пользователями.
Посылки не видны? Если да — могу выложить на pastebin, например.
Да
Выложил все на Pastebin
или у числа L на этой позиции стоит 0, или у числа L на этой позиции стоит 1, а переменная fl1 показывает, что когда-то был выбран бит, который больше соответствующего бита в числе R.
Имелось в виду "соответствующего бита в числе L."?
Безусловно. Спасибо, исправил.
Мнение капитана про задачу D.
Пускай L < 2i ≤ R < 2i + 1. Тогда ответ —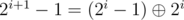 , т.к. более старшие биты мы затрагивать не умеем. Если 2i ≤ L ≤ R < 2i + 1, у нас во всех числах старший бит расположен в i-ой позиции, значит, он все равно при XOR'е сократится и можно без изменений перейти к отрезку [L - 2i;R - 2i]. Проходимся по i сверху вниз, получаем ответ.
, т.к. более старшие биты мы затрагивать не умеем. Если 2i ≤ L ≤ R < 2i + 1, у нас во всех числах старший бит расположен в i-ой позиции, значит, он все равно при XOR'е сократится и можно без изменений перейти к отрезку [L - 2i;R - 2i]. Проходимся по i сверху вниз, получаем ответ.
Ну или даже проще, нас интересует первый бит, который не совпадает у L и R, потому что после него можно поставить все 1 ( взяв в первом числе на этом месте 1, а на остальных нули, а во втором наоборот), и на Java получается очень красиво в одну строчку
Да, красивая реализация...
Опишу жадное решение D, которое сдали многие участники (включая меня).
Выпишем l и r в побитовой форме в порядке "от старших битов к младшим" и приведем их к одинаковой длине. Заметим, что первый единичный бит ответа не может лежать внутри общего префикса наших двух битовых строк. Т.о. найдем первое несовпадение (пусть это будет i-ый разряд от конца). Заметим, что 2i и 2i - 1 гарантированно лежат на отрезке [l;r], а т.к. все биты этих чисел различны, их XOR равен их сумме, и при этом является максимально возможным. Т.о. получим, что наш ответ равен 2i + 1 - 1.
Реализация на Java: 3184866.
UPD. И вновь я опоздал :(.
Добавил такое решение в разбор.
шикарнейший контест и разбор. Спасибо
в Е еще можно было sqrt-эвристику написать: разбить на sqrt блоков запросы и погнали
мне вот интересно, неужели автор не заметил, что в Д ответ всегда 2^k-1? или заметил, но решил не разбираться с этим?
Я действительно не заметил этот факт
Спасибо за разбор. Читая разбор и условие задачи E главное понять что "каждая вершина(кроме 1) имеет степень не более 2", это значит что у вершин кроме корня, максимум один ребенок — то есть единственное ветвление находится в корне.
Простите, а почему ето правда для Фенвика ?
Потому что мы храним в Фенвике не значения элементов массива (
a[i]), а разности между соседями (a[i] - a[i - 1]). Нетрудно понять, чтоa[i]находится просто как сумма на i-ом префиксе, а прибавление на отрезке [l; r] осуществляется как раз с помощьюadd(l, val)иadd(r + 1, - val).знаете ли Вы еще какие то интервальные задачи которые можно решать фенвиком ?
AlexanderBolshakov вобщем-то уже ответил на ваш вопрос. Кое-что все-таки добавлю от себя.
В задаче C мы могли поддерживать массив d просто как массив (не используя специальных структур данных) потому, что ответы на запросы, аналогичные запросам типа 1 нам нужно было знать после того, как мы обработаем запросы типа 0. Здесь же все происходит онлайн, ведь запросы идут в перемешку. Если бы мы в задаче Е использовали обыный массив, тогда изменения происходили бы за время О(1), зато пересчет значения элемента выполнялся бы за O(n), и суммарно алгоритм бы работал за время O(QN). Если же для аналогичных целей использовать дерево Фенвика, то тогда оба запроса буду выполнятся за время O(logN), да еще и с очень маленькой константой, чего более чем достаточно для решения задачи.
can somebody post the tutorial in English !! thanks much appreciated :)
I'll translate the editorial as soon as possible. I'll try to do it today.
В задаче Е, как я понимаю, если запрос типа 0 задевает корень, то мы должны обновить полностью все цепочки; однако в разборе "подразумевается" что в любом случае запросы обрабатываются за O( logn ). Можете поподробнее объяснить, как именно можно быстро обновлять все цепочки сразу ?
там же есть в разборе: "Дерево, заведенное для корня в некотором смысле является глобальным — значения, которые в нем присутствуют, актуальны для всех цепочек."
In maximum XOR question: In the bit representation of l and r if the leftmost difference in their bit patterns occurs at the nth position isn't the answer simply 2^n-1?
It's true (if n is 1-indexed, of course). I described this solution in editorial.
Nice editorial and clear explanation!! One thing that I want to know that what the following code segment do? And how can I have my own "whatever it is called :p"? Thanks :)
It's a preprocessor definition. You can read about it here: http://msdn.microsoft.com/en-us/library/hhzbb5c8(v=vs.80).aspx or google it elsewhere.
This block redirects stdin to file and starts measuring execution time of my program. Because of preprocessor definitions, this code does not execute on a judging system, but I can use it locally.
wah, thanks for this editorial, the explanation is very clear :)
Love the alternate solution to D !
Guess it could be applied to a harder question where L and R were represented in binary form with a string of length <= 10^6.
I wrote a detailed post about Problem D here. Let me know if you have any doubts or want to discuss further :)
nice explanation bro thanks
In the code for E, can you please explain what the variable t is doing ? Not able to understand.
The variable t holds all of the binary index trees (one for each chain and one for the root)
Wow, it's nice to see that someone is actually working on the problems from that contest even after all these years :)
Thank you for your reply. I even wrote a blog post about your D :)
I'm trying to do it with segment trees as I'm not that comfortable with BITs. I'm struggling with dynamically allocating memory to each tree :\
Segment trees are also perfectly suitable for this task. You can easily allocate memory in a very similar manner — just store segment trees in vectors and resize them appropriately (usual stuff — suppose you have n elements in your tree, then find the smallest k such as 2k ≥ n and allocate memory for 2k + 1 elements)
Thank you for your assistance.
Please check my blog about your problem :)
Use some mathematics for Div2 D and you will be able to find the solution in just few lines of code. My Solution:- 72932119 For a detail explanation reply to this comment.
why is my code getting wrong answer for c question test 7 .. i have done similar to what is mentioned in editorial https://mirror.codeforces.com/contest/276/submission/94873267
Can Div2 C be solved using segment tree ? I tried but getting TLE on testcase 7
Yes, I solved it based on segment tree. At first, we use segment tree to find out the number of queries for each element. Then, we could adopt a greedy algorithm to compute the final answer.
hello i'd like to share my solution for problem C