Hi, all. There was an interesting problem from Codechef's August 19 Long challenge. In short, you are given vector k and vector c, and you have to find vector x, such that x1⋅k1+x2⋅k2+…+xN⋅kN=0. and √x1+c1+√x2+c2+√+…+√xN+cN is max (of course if every expression under a root is non-negative).
There have been great analytical solutions to this problem, and the editorial mentions approaches like using Cauchy-Schwarz Inequality and alike.
I have a feeling that the solution might represent something geometrical. Given the first equation, we can see that vectors x and k are perpendicular. I can't interpret the second expression in geometrical terms, but from drawing few examples, X seem to be parallel with the perpendicular, drawn from the point C to the vector K, with the length, multiplied by some number
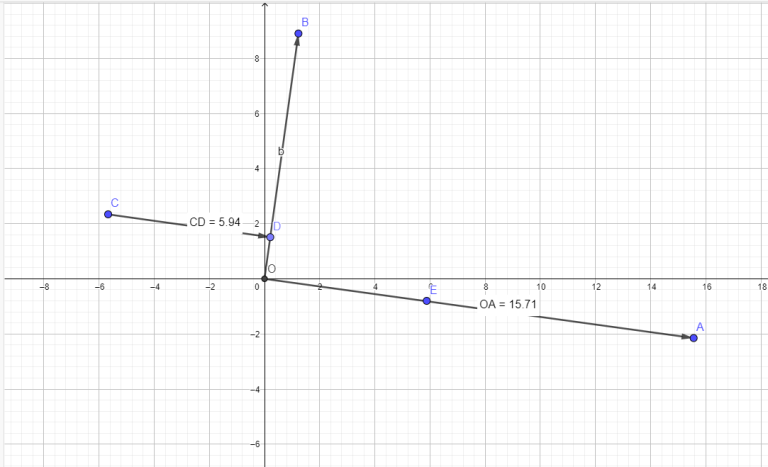
In this picture N=2, K = OB, C = OC, the resulting X = OA. CD is the height, dropped from the C onto the vector OB, and the result is parallel to it, with some scaling factor.
If anyone can help me interpret vector X in geometric terms — i am very curious.










