Hi!

289A - Polo the Penguin and Segments

Solution. First of all, we need to count, how many integers are inside given segments at the beginning. Since they don't intersect and even touch, no integer point can belong to more than one segment at the same time. This mans that starting value of segments is .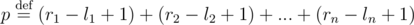

If k divides p, then answer is 0 — we don't need to do anything, it's already done. But if it's not true, we need to know the minimal number of turns to make k divisor of p. Since we can in single turn increase p by 1 (by decreasing the left point of the leftmost segment), this number is equal to .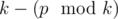

Note. Note that just output 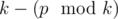is not enough: you need to pay attention for case when 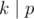, or just output .

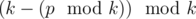289B - Polo the Penguin and Matrix

Solution. First of all, we need to know when the answer is -1. For that you should notice that after any operation on number z, value 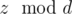doesn't change. Indeed, 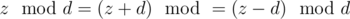. This means that there is not answer if there are two different points for which 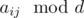is diffrent.

Now we can transform our problem a bit. We can just write down all integers from matrix n × m to one array b of size k = n × m and sort them all in non-decreasing order. It is not hard to notice that in some of the optimal solutions, all number are at the end equal to one of the number for starting array. But also, it is optimal to make all number equal to 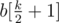(median element). Why to median? Suppose that we make all numbers equal to non-median element with index x. Then if |x - (k - x)| > 1 (i. e. from one side there are more elements than from another + 1). So, by moving out element more to median, we can make result better.

After we know, to which number we should bring all, the answer is just 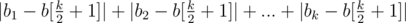, divided by d.

Note. There is also full solution with complexity O(n²m²).

288A - Polo the Penguin and Strings

Solution. To solve this problem we need to find out some contruction of resulting string. But first of all, we need find out when there is no result. Obviously, if k > n, there is not result — you cannot build string of length n with more than n characters. Another one case is when k = 1 and n > 1 — there is no answer in that case also.

Consider that k = 2. It's really easy to see that answer for such case is a string of form abababab.... To construct string for k > 2 you need to add some extra characters — c, d, e.... To make string lexicographically smallest, you need to add that characters as close to the end as we can. And the best bet here is abbabab...abacdefgh.... So, we need just to add characters c, d, e, f... (i. e. k - 2 characters from c) to the end of the string.

288B - Polo the Penguin and Houses

Solution. Since k ≤ 8 you can solve this problem using brute force. This means that you can recursively construct all possible k^k possibilities of first k assignments. (For k = 8 this is equal to 16 777 216.) For each of that assignments you need to check whether it is correct or not (by problem statement). Ths can be simply done using loops.

When you know the number of assignment for the first k tables (let it be f(k)), all you need to do is to count the number of assignment for the rest n - k plaques. Since there should bo no path to 1, there should be no path to any of first k houses, so at each plaque for houses from k + 1 to n there can be any number from k + 1 to n, inclusive. There are (n - k)^n - k such possibilities. And hence the total answer is f(k)(n - k)^n - k.

Note. There also exists solution with dynamic programming, and also there exists formula for f(x). You can read about it more here, here и here.

288C - Polo the Penguin and XOR operation

Solution. Since we need to maximize the result, we need to find such permutation, for which the least number of bit disappear. (We consider bit disappeared if it was 1 both in i and p_i, so in it is 0). It turns out that for each n there is such permutation that no bit disappear. How to build it? We will be solving problem by iterations while n > 0. On each iteration, we need to find the biggest (the leftmost in binary representation) bit which is not 0 in binary representation of n and denote it position (bits are numbered from 0) by b. Now we need to find integer m — minimal integer from 0 to n, inclusive, such that b-th bit is also 1 in it. 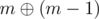After that you can see (look image below), that at no bit disappear, at no bit disappear, ..., at 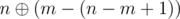no bit disappear. So, it is good to assign exactly that integers to our permutation, i. e. p_m = m - 1 and p_m - 1 = m, p_m + 1 = m - 2 and p_m - 2 = m + 1 and so on. After that assign value m - (n - m + 1) - 1 to n and go to next iteration.

Now when we know how to build permutation and that no bit disappear, the value of the answer is equal to .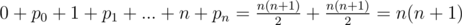

288D - Polo the Penguin and Trees

Solution. As always in such problems, root our tree at some vertex, for example vertex with number 1. We need to find out, what will happen when we have already chosen one path. Obviously, after deleting all vertices and their edges from that path, tree will disintegrate in some set of trees. Denote their sizes by c₁, c₂, ..., c_k, where k is the number of trees. Then the number of ways to choose the second path is equal to 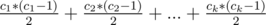. This gives us O(n²) solution — just to brute force all pathes and count the number of second paths by this formula. We need to do it in O(n). To do so, dfs our graph and fix some vertex during dfs, we will consider this vertex as the last vertex in the first path. Now we need to find the sum of above formula for the rest of the vertex. Here you can separately solve this problem for all vertex inside subtree of current vertex and for the rest of the vertices. For subtree vertices, you can, after finding the answers for all vertices of subtree, find the answer for root of subtree. To do so, you need to iterate all edges from current vertex and sum up results for that vetices. Also you need to add the sum of values 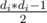multiplied by the number of vertices in subtree, where d_i are all sizes of subtrees of vertices from current vertex, not including from current edge). You can use some partial sums of something like that to make it linear. For the rest of the vertices (not in subtree) it is actually similar, but a bit harder. Here you need to keep current result as a parameter of dfs and when you entering some vertex you should add some additional counts to the current sum (similarly as in first case).

Note. Also, you can find the number of bad pairs of pathes and subtract it from the total number. Also some divide and coquer solution exists, you can think about it.

288E - Polo the Penguin and Lucky Numbers

Solution. In this problem there are a lot of different formulas, most of them are for optimizing solution and making it lenear. Editorial shows just a general idea because it's pretty hard to explain all of them and good for you to derive it by yourself. If you have any questions — write them all in comments.

Denote by a₁, a₂, ..., a_n all lucky number from segment. First of all, we need to do reduce the problem a bit. Let we have some fixed digit (pos, d), i. e. position of this digit is pos (from 0 from right to left) and value is d (4 or 7). Then, for all a_i (1 ≤ i < n) such that pos-th digit of a_i is equal to d, we need to add a_i + 1 × d × 10^pos to the answer. Now we can see that problem can be reduced to the following. For each fixed digit (pos, d) find the sum of all a_i such that a_i + 1 on the pos-th position has digit d. Obviously, we can solve the problem for 1..l and 1..r separately and then subtract the first from the second — that will be the answer.

How to find such sum among all lucky numbers of some length but less than some lucky number x? We will describe the general idea. Any lucky number, less than x has some common prefix with x, then one digit is less than the corresponing in x (i. e. it is 7 in x and 4 in another integer) and the rest of the digits are arbitrary. So, by iterating all such positions where is the first digit less than in x, we can, using the fact that the rest of the digits are arbitrary and some formulas and precomputations, compute the results for each position and digit.