Greetings,
I have found a couple of very interesting math problems on the Dhaka 2008 problemset:
The first one is about counting in how many ways you can put a right triangle over a square taking into account some constraints(I know it has to do with prime factorization). The second one is about computing the following function modulus 10007:
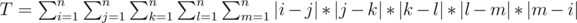
and n ≤ = 2 * 109
I would find very useful any hint/comment that you can give me about these problems.
Thanks in advance.











Hint for the second problem: There exists an exact polynomial to calculate T(n). However, the method to discover it would be heavily related to math. Instead, by knowing it would be a degree 10 polynomial, we can use Newton's Divided Difference Method. One more thing to note is that T(n) = T(n % 10007), so we only need the first 10007 values of T.
Thanks for replying flashmt. Your hint was very helpful, now I see how to solve the problem but I find very difficult to come up with an idea like that for solving a problem.