Hello Codeforces!
On Jan/14/2020 17:35 (Moscow time) Educational Codeforces Round 80 (Rated for Div. 2) will start.
Series of Educational Rounds continue being held as Harbour.Space University initiative! You can read the details about the cooperation between Harbour.Space University and Codeforces in the blog post.
This round will be rated for the participants with rating lower than 2100. It will be held on extended ICPC rules. The penalty for each incorrect submission until the submission with a full solution is 10 minutes. After the end of the contest you will have 12 hours to hack any solution you want. You will have access to copy any solution and test it locally.
You will be given 6 problems and 2 hours to solve them.
The problems were invented and prepared by Roman Roms Glazov, Adilbek adedalic Dalabaev, Vladimir vovuh Petrov, Ivan BledDest Androsov, Maksim Neon Mescheryakov and me. Also huge thanks to Mike MikeMirzayanov Mirzayanov for great systems Polygon and Codeforces.
Good luck to all the participants!
Our friends at Harbour.Space also have a message for you:

Hi Codeforces!
As a special prize for the Educational Round 80, we would like to invite the top 3 participants to take part in our Hello Muscat ICPC Programming Bootcamp, which will take place in Oman, from March 19 to March 25, 2020. The prize will cover the participation fee, accommodation, and half-board meals for the entire duration of the bootcamp (except flights)!
There are three requirements to satisfy:
- You took part in at least 10 rated contests on Codeforces
- Your max rating should be less than 2400
- You should be eligible for ICPC and/or IOI 2020+
Good luck to everyone!
Note: If you really want to participate, but cannot afford the participation fee, get in touch with us to request a supporting letter for you to show to your university, employer, or local companies. With this letter, you are opening the possibility of being sponsored by them to attend the bootcamp.
Please fill out this form and we’ll send you the support letter within 3 days!
Congratulations to the winners:
| Rank | Competitor | Problems Solved | Penalty |
|---|---|---|---|
| 1 | isaf27 | 6 | 150 |
| 2 | FSTForces | 6 | 167 |
| 3 | jiangly | 6 | 178 |
| 4 | ko_osaga | 6 | 179 |
| 5 | jhnan917 | 6 | 184 |
Congratulations to the best hackers:
| Rank | Competitor | Hack Count |
|---|---|---|
| 1 | surung9898 | 59:-2 |
| 2 | stdmultiset | 35:-1 |
| 3 | B2ej5SjC | 30 |
| 4 | spectre_1502 | 21:-1 |
| 5 | Dilemma27 | 20:-4 |
And finally people who were the first to solve each problem:
| Problem | Competitor | Penalty |
|---|---|---|
| A | okwedook | 0:01 |
| B | neal | 0:04 |
| C | ko_osaga | 0:06 |
| D | RUSH_D_CAT | 0:07 |
| E | peach | 0:17 |
| F | jiangly | 1:13 |
UPD: The editorial is out










Your max rating should be less than 2400I hope it's not a typo.Hi aryanc403! It is not a typo :)
The prize is for users who have never been "red". Good luck in the contest!
I wonder why Div1 people are not listed as unofficial participants (with a * ) for educational rounds. Is it intentional?
I think they don't have the star because they can hack official participants in hacking phase. In regular div 2 rounds the rooms for official and unofficial participants are separated.
The hacking phase is only after the round. Div3 contests work in the same way but unofficial participants get a star.
The first educational rounds were not rated so everyone was an official participant. The educational 33 was first rated one. They just didn't change how the scoreboard is shown.
Waiting for good problems to learn new concepts.
hope contest gap will decrease
Seems it will be a high-quality contest
contests by awoo are always fun.
Why always Educational's blog had a few upvotes :( These Rounds are really educational, interesting and helpful . They are underrated i thnik .
I think your comment is overrated
MikeMirzayanov it seems the https certificate of
pubsub.codeforces.comis expired and my internet security is constantly blocking the connection to the same, saying it is insecure. Did the certificate expire recently?Every second which i spent with codeforce gives me an infinite pleasure.
You should seek help
"The statement is not available" — m2.codeforces.com
How to solve C?
Suppose we take two arrays a,b such that the ascending array ends with number i, and descending array ends with number j. If we count all ascending arrays ending in i and descending arrays ending in j, then we have the answer for this specific i,j.
Once we can do that, we can simply iterate over all i,j (with $$$i <= j$$$) and get the total answer by summing these values.
So the question is, given an ascending array ending in the number i, with length m, how many such arrays can there be? We can see that such an array can be like 11122233...i, or can be 1222333444...i, or iiiiiiii...i. So let $$$a_1$$$ be the number of elements that are 1, $$$a_2$$$ be the number of elements that are 2, and so on till $$$a_i$$$. Then the answer is equivalent to the number of integer solutions to $$$a_1 + a_2 + a_3 ... a_i = m$$$, where $$$a_i >= 1$$$ and the rest are $$$geq 0$$$. The answer to this is through stars and bars $$$C(i + m - 2, m- 1)$$$. Similiarly you can do for j (you need numbers from j to n), and you will get something like $$$C(n - j + m - 1, m - 1)$$$. and then multiply and sum to calculate the answer.
Can you explain with more details?
68799118
Exactly what is the confusion? The formula, or the approach?
approach
The last element of the ascending array must be smaller than or equal to the last element of the descending array. I iterated over all unique (last ascending, last descending pairs), and for each such pair, calculated the answer if the last element of each array was as given.
Could you explain to me the formula for stars and bars?
Thanks
Amazing explanation ! The critical observation here is that the last element of $$$A$$$ is smaller than the first element of $$$B$$$
$$$A_1 \le A_2 \le ... A_m \le B_m \le B_{m - 1} \le ... \le B_1$$$
And then you explained how to count the number of non-increasing and non-decreasing sequences of length $$$m$$$.
Beautiful !
The no of integer solutions of a1+a2+a3+...+ai=m is given C(m+(i-1),m) but why did you write C(i+m−2,m−1)? I think you took m=m-1, but why?
Because $$$ a_i >= 1$$$, as the sequence ends in i. Therefore we can make $$$a_i >= 0$$$ and take m = m — 1.
Ok.Got it. Thanks
The answer can be proven to be
Can you give the proof?
So say the numbers are $$$1\leq a_{1} \leq a_{2} \leq .... \leq a_{m} \leq b_{m} \leq b_{m-1} \leq .... \leq b_{1} \leq n$$$.So basically we have to select $$$2m$$$ numbers from $$$[n]$$$ which may not be necessarily distinct.Let the numbers be $$$1\leq c_1 \leq c_2 \leq ..... \leq c_{2m}\leq n$$$(I have taken the notation $$$c_i$$$ just for convinience).Now consider the sequence $$$d_i=c_i+i$$$.Clearly there is a bijection between $$$c \Longleftrightarrow d$$$.But note that $$$2\leq d_1 < d_2 < ... d_{2m}\leq n+2m$$$.Now we just have to select $$$2m$$$ numbers from $$$[2,n+2m]$$$ or scaling down choose from $$$[1,n+2m-1]$$$.This can be done in $$$\binom{n+2m1}{2m}$$$
I didn't understand sequence di=ci+i part.Can you please elaborate it.
See for all $$$1\leq i\leq 2m-1$$$ $$$c_{i+1}\geq c_i\implies (d_{i+1}-{i+1})\geq (d_i-i)\implies d_{i+1}\geq 1+d_i>d_i$$$.Also $$$c_1\geq 1\implies d_1\geq 2$$$ and $$$c_{2m}\leq n\implies d_{2m}\leq n+2m$$$.Hope this is clear.The bijection part just asserts that the number of ways of choosing $$$2m$$$ numbers of $$$c_i$$$ form is same as that of choosing $$$2m$$$ distinct terms from $$$d_i$$$
How do you think about declaring di=ci+i. Is it a common practice to remove equality?
Its fairly well known in the math community and yeah I can understand that this feels like magic but its a nice trick.If you read about Stars and Bars then this becomes easier to grasp.
Any good resources for strengthening combinatorics for CP? I did solve the problem but wasn't able to come up with the closed form/
Yes, i too am is in search of a good resource to improve in combinatorics used in CP
Beautiful Idea. Especially to remove the inequality !
Since we have to choose a non-decreasing sequence (Xi) of length 2m. 1<=Xi<=n.
consider this sequence... S:= 1 1 1 1.......2 2 2 2......3 3 3 3....n n n n n..... (where i i i… repeats 2m times). Now we have two find no of ways of choosing a non-decreasing sequence of length 2m form S. This is exactly same as finding no of solution of the linear equation X1 + X2 + X3 +.....+ Xn = 2m. where Xi denotes how many time i appears in the chosen sequence. so clearly Xi can takes value from 0 to 2m. and hence this linear equation can be solve by standard classical mathematics i.e. finding coefficient of 'x^2m' in the polynomial P(x)=(1+x+x^2+...+x^2m)*(1+x+x^2+...+x^2m)*....*(1+x+x^2+...+x^2m)... n times for each Xi.
One more trick:= (1+x+x^2+...+x^2m) can be replace by (1+x+x^2+...+x^2m+....) infinite sum since x^(2m+1) and higher power doesn't contribute in coefficient of x^2m(that we are interested in)
Now we are done P(x) reduces to p(x)= 1/(1-x)^n
and there is standard famous formula for ...
coefficient of x^r in 1/(1-x)^n is — (n+r-1)C(r).
Since r=2m here so answer is (n+2m-1)C(2m).
check this 68817461
Beautiful solution + explanation, Thanks.
can you please explain a little bit why we can assign any number large than a[i-1] even though the i is larger than m, I'm confused because b should be decreasing
ah I see, thanks!
A saver!! thank you so much <3
How did you think. Nice solution :)
:)) cin >> n >> m; cout << C(n + 2 * m — 1, n — 1);
Can you explain ?
count the number of ways to arrange number from 1 to n into array 2 * m length is sorted in non-descending order. That is combination with repetition C(2 * m + n — 1, n — 1)
Suppose m=6 ,A=[1,2,2,3,4,5] and B=[9,8,7,7,5,5] Now make a new array X of size 2*m whose first m elements are same as A and next m elements are same as B but in reverse direction. So new array becomes- X= [1,2,2,3,4,5,5,5,7,7,8,9] The new array X is non decreasing in nature. So basically for every correct pair of A and B, its X will be non-decreasing in nature. So, you basically have to find number of possible non decreasing array of size 2*m whose elements are between 1 to n. This could be easily calculated using dp.
Code- (http://mirror.codeforces.com/contest/1288/submission/68824571)
The dp solution I implemented is O(N^2 * M). Is there a faster time-complexity solution that involves dp?
Same
I implemented it in O(n*m^2), first choosing the maximum element as i which can reside in first array and then second array can choose elements only from n-i+1 numbers and then use stars and bars technique for both the arrays
My solution : https://mirror.codeforces.com/contest/1288/submission/68829446
I did the same DP. The states of DP maintain a range of possible values for both sequences.
Actually the range itself doesn't matter, just its length — we use it to check if the range is non-empty after increasing the lower bound or decreasing the upper bound.
Then it's easy to code the DP in $$$O(n*m)$$$. my cpp code
The final statement that you wrote can be solved using combinatorics. I claim that any strictly increasing sequence with elements between 2 to n+2m, can be converted into non decreasing sequence with elements between 1 and n, by decreasing each element's value by its index. Since the number of ways for the first problem is same as the number of ways to select 2m numbers from n+2m-1 numbers, that'll be our answer for the second question as well. Tl:Dr: Answer is C(n+2m-1,2m).
How to solve D?
Use bit masks to know for each line the minimum value of each mask of it, then combine the best mask and ((1<<m)-1 ^ mask) to find the answer
when you say "mask" , what you really mean ?
I mean all subsets
You do a binary search on the answer. Then for checking if an answer $$$x$$$ is valid, you can make a $$$m$$$ bit mask for every array in which $$$i$$$th bit is $$$1$$$ if $$$a[i]$$$ is greater than $$$x$$$. The problem now is to find two arrays so that bitwise or of the mask of two arrays is equal to $$$2^m - 1$$$. For that you can just fix one array and brute force all possible masks which complement current mask (which are less than $$$2^m$$$) and find if the mask is among the mask of all arrays. If there is one then the answer $$$x$$$ is valid otherwise no.
Thanks, it is very clear. Binary search over x is log(1e9)=1e3. And n=3e5. So, 3e8 in total, I thought it would TLE so did not even consider this way. Brute over bit masks is cool, I did not get to this point on contest. Thanks.
log(1e9) = ~30 not 1e3
My bad
log(1e9) * 8 * 3e5 = 30 * 8 * 3e5 ~= 1e8. A bit better =)
The time limit for this question is 5 !
I got TLE on test 21 :( I think I used some unnecessary sets that added an undesired log factor
I also used unnecessary sets. Was lucky to have got it passed in 4.7 seconds. My complexity was $$${2^m}*n*m*\log{10^9}$$$. Later I realized it was possible to do it in $$${(n*m+{4^m})\log{10^9}}$$$. The latter passed in 0.9 seconds.
Thanks a lot RetiredProgrammer .
Can you explain a bit how this solution works. Actually I don't understand the part where we find two array so thats bitwise or of the mask of two arrays is equal to 2^m−1. I have not much idea about bismask but I know in k size bit we have store something in every bit whether the postion is true or false. Set bit 1 , 0. This type of basic idea.
Thanks again :)
Assume you are trying to find an answer that has score of at least $$$x$$$. We can now convert each array into a mask of $$$m$$$ bits where the $$$j$$$-th bit is $$$1$$$ if $$$a_{i, j} \geq x$$$, and $$$0$$$ otherwise.
As there are only $$$2^m \leq 256$$$ distinct possible masks, you can easily store, for each mask, the index of an array that matches it, or a "nil" value if no arrays match it. Then bruteforce pairs of masks; if they both have valid indices and complement each other (i.e. $$$mask_a \vee mask_b = 2^m - 1$$$, where $$$\vee$$$ is the binary "or" operator), there is a result with a score of at least $$$x$$$.
We can then binary search for the maximum $$$x$$$ score that returns a valid answer.
My final time complexity is $$$O((nm + 2^{2m})\log(\max a_{i,j}))$$$ (68838510)
I've tried binary search + bitmask solution and it got accepted. Then I see the dp tag on this problem. Is there any dp involved here? or there is another dp solution?
Tags only imply that it's possible to use a technique to solve the problem, and not necessarily that the technique must be used to solve the problem. I'm not exactly sure how to use DP to approach this problem though.
Yeah, even the editorial uses the exact approach described by you. No dp at all.
It seems like they have written dp as there is a small dp modification which can reduce the comp to (nm+2^m)(log(max))
Hm. I can see how to reduce it to $$$O((nm + 3^m) \log \max a)$$$ (for each bit position, there are three valid pairs of bits), but not $$$... 2^m ...$$$
For each array and for each mask (out of $$$2^m$$$ of its indexes) calculate a minimum value. Then go through the input and for each array $$$i$$$ enumerate all masks $$$M$$$. Between all masks $$$M$$$ calculate maximum value of minimum(calculated minimum for mask $$$M$$$ of array $$$i$$$, maximum of calculated minimums for mask $$$2^m - 1 - M$$$ of all already processed arrays). The second value can be updated on the fly.
Consider desired $$$i$$$ and $$$j$$$ and their corresponding arrays $$$a[i]$$$ and $$$a[j]$$$. For each $$$k$$$ $$$(1..m)$$$ a value from either $$$a[i]$$$ or $$$a[j]$$$ is bigger and thus selected for the array $$$b$$$. This splits all indexes $$$k$$$ in $$$1..m$$$ into two parts: those where $$$a[i][k] \ge a[j][k]$$$, and those where $$$a[i][k] < a[j][k]$$$. These parts are complementary masks of indexes, and resulting value will be minimum(minimum value in some mask of array $$$i$$$, minimum value in complementary mask of array $$$j$$$). And you are maximizing this value.
Veeeeery interesting!
Thanks a lot for your insightful explanation to D ! I learnt a lot from this beautiful problem !
Clearly, Numberphile made this contest
Can anyone share a solution to F?
how to solve B
The answer for a given pair (A, B) is A * the count of numbers of the form 9, 99, 999, 9999, 99999.... that are less than or equal to B.
Basically a pair (a,b) is valid if and only if b is of the form 99...9. Therefore, you just need to count the number of numbers of this type between 1 and B and multiply by A.
a*b+a+b=a*10^p+b ==>b+1=10^p
Fix the length of $$$b$$$ and name it $$$i$$$. It can be between $$$1$$$ to $$$10$$$. Then we have $$$a \times b + a + b = a + 10^i \times b$$$. It simplifies into $$$b = 10^i - 1$$$. So no matter what $$$a$$$ is, $$$b$$$ is $$$10^i - 1$$$. So just check if $$$10^i - 1$$$ is between $$$1$$$ and $$$B$$$ and if it is add $$$a$$$ to the answer.
Can someone please explain the solution to D ?
Happy Hacking in 1288F - Red-Blue Graph 68818026 !!! System test passed!! awoo it should be ok?
Whould you be so kind to explain what is going on in your solution?
Simplex_algorithm
Should've set the constraints higher :^) It's ok I guess but minimum cost circulation was the intended solution.
How to solve B
Math shows that $$$b$$$ in the formula has to be of the form 999999...9, and $$$a$$$ doesn't matter.
a*b+a+b=conc(a,b). Let number of digits in b be d,then conc(a,b)=a*(10^d)+b. a*b+a+b=a*(10^d)+b a*b=a*(10^d-1), a!=0. b=10^d-1. hence b=9,99,999,.....99999999,as b<=10^9. So find the number of b's less than B,call it temp. Answer is temp*a.
How is this not TLE in A? https://mirror.codeforces.com/contest/1288/submission/68782530
Because when n > O(sqrt(d)), It always success. so that code must done O(sqrt(d))
By looking closely at conditions given in $$$C$$$, we see that $$$a_{1} <= a_{2} <= .... <= a_{m} <= b_{m} <= b_{m-1} <= .... <= b_{1}$$$.
So, why does choosing any $$$2*m$$$ elements not work, i.e. why is $$$n^{2*m}$$$ wrong. I don't understand, can someone please help me clear this up.
The reasoning isn't wrong at all. Choosing $$$2*m$$$ elements that satisfy that condition would work. But $$$n^{2*m}$$$ is not the way to count that, since you are counting sequences that are invalid. This number is the total number of sequences of lenght $$$2*m$$$ some of which doesnt satisfy that condition.
Yeah, I just realised this is overcounting all permutations. Thanks for your reply.
You are overcounting.Say for eg if the $$$a_i$$$ and $$$b_i$$$ are $$$1,1,2,2$$$ then you count this as number.Then you also count $$$1,2,1,2$$$ and all permutation of it when you shouldnt be.To count the desired number we have to use stars and bars.
Yeah, I realised it now. Thanks for your reply.
.
Am I the only one who did C with 2-D prefix sums?)
no ...i also did the same
Me too, and also KrK. Though it was a very easy formula :(
nope
Can you please share your approach ?
Let dp[k][i][j] will be number of valid arrays with length k and with a[k]=i and b[k]=j; So to get dp[k][i][j] we need all the dp[k-1][l][r] with l<=i and r>=j. How can we calculate it fast? Let's do 2*D prefix sums on dp[k-1][i][j] for all possible i and j. So formula is: dp[k][i][j]=pref[i][n]-pref[i][j-1]. Where pref[x][y] is sum of all dp[k-1][i][j] where i<=x and j<=y. https://mirror.codeforces.com/contest/1288/submission/68798026
I simpler way is including transitions that deal with it.
$$$dp[k][i][j] = dp[k-1][i][j] + dp[k][i + 1][j] + dp[k][i][j - 1] - dp[k][i + 1][j - 1]$$$
And we get a nice $$$O(n^2*m)$$$ solution.
We can further improve it because $$$i$$$ and $$$j$$$ don't matter just $$$j-i+1$$$. That makes it $$$O(n*m)$$$. code
hey excellent transition. Could you provide a little explanation on why i , j dont matter just length j-i+1 enough . did u mean dp[k][3][5] == dp[k][4][6] ?
Yes, $$$dp[k][3][5] == dp[k][4][6]$$$.
We just use $$$i$$$ and $$$j$$$ to check if the range is non-empty, $$$dp[k][i][j] = 0, \text{if }i > j$$$.
You can also think that we will always normalize the range so that $$$i = 1$$$, eg [6, 10] -> [1, 5]. As $$$i$$$ is constant it can be remove from the state.
Can you please explain the transition formula a bit more.
I solved using suffix sum. My relation came dp[i][j]= dp[i-1][j] + suffix_sum[i][j].
Me too, buddy ^.^
"You should be eligible for ICPC and/or IOI 2020+" I have second priority of bootcamp invite letter... But could not participate due to the above conditions.... So sad ;-;
I used binary search for D, is there any other method to do it in the given constraints?
My idea for problem A:
Getting $$$\min \left(x + \left \lceil \dfrac{d}{x + 1} \right \rceil \right )$$$ is the same as getting $$$\min \left(x + 1 + \left \lceil \dfrac{d}{x + 1} \right \rceil \right ) - 1$$$.
Then let $$$a = x + 1$$$, we should get $$$\min \left(a + \left \lceil \dfrac{d}{a} \right \rceil \right )$$$. Because we know $$$a + b \ge 2\sqrt{ab}$$$, I thought $$$\min \left(a + \left \lceil \dfrac{d}{a} \right \rceil \right )= \left \lceil 2 \sqrt{d}\right \rceil$$$. My code is here:
But now I think there's something wrong with it, that's becase of $$$\mathrm{ceil}$$$. Could you please HACK my solution, or tell me if it's right?Thanks.
I just made sure to check the area +/-1 of sqrt(d) just to be safe.
Can you explain why did you take the ceil of sqrt(d)*2 ?
a + (d/a) >= 2*sqrt(d)
so, a + ceil(d/a) >= 2*sqrt(d) ?
$$$a + \dfrac{d}{a} \ge 2 \sqrt{d}$$$ is of course right, and $$$a + \left\lceil\dfrac{d}{a} \right \rceil \ge 2 \sqrt{d}$$$ is also obvious (Because $$$\left\lceil\dfrac{d}{a} \right \rceil \ge \dfrac{d}{a}$$$ ). But I can't proof $$$a + \left\lceil\dfrac{d}{a} \right \rceil \ge \left \lceil 2 \sqrt{d} \right \rceil$$$ .
I'm wondering it. That's just the reason I post this comment. But it seems that I have passed the system test?
Couldn't it be the case that 2√d <= n but a + d/a > n?
How to solve E?
Minimum position is 1 or i, we only need to calculate max now. Let's find first position of i, before i becomes first every number larger than x changes position by one, so it's 1 + number of distinct integers larger than i before this position. Now between 1st position and 2nd, 2nd and 3rd, and so on, it's position is just 1 + number of distinct integers in range. This stuff can be calculated with segment trees.
how to do this with segment tree?
It can be solved using persistent segment trees. Here
You can also do that without persistency, fenwick tree is enough
Straight forward implementation of the idea shared by Len. https://mirror.codeforces.com/contest/1288/submission/68828821
Hi,can you explain detailedly? I can't understand it.
Also, you could simulate the whole process.
In the beginning, $$$min_i = max_i = i$$$. When some element moves to the front, you set $$$min_i = 1$$$ and $$$max_i = max(max_i, a)$$$, where $$$a$$$ is its current position (because it is the element's rightmost position before it will be moved to the front). In the end, you update $$$max_i$$$ for every $$$i$$$ again, based on the positions of the elements in our sequence.
The insertion/deletion operations can be done with ordered_set, treap in $$$O(n + m \log n)$$$, or with split-rebuild sqrt decomposition in $$$O(n + m \sqrt n)$$$, 68820376, if you want to have fun.
P.S. This approach is quite structure-heavy, less thinking, more implementing (which makes it not really beautiful).
Haha, I set time limit generously to let any sqrt/log^2 distinct value queries pass but I'm glad this passes as well :D
Fenwick tree of size $$$n+m$$$ works as well, probably a bit easier to implement.
Fenwick tree+PBDS solution: Code
In problem A, shouldn't be the output of:
1
18 88
be "NO"? Shouldn't the minimum days required be 19 and not 18? My hack was unsuccessful for a solution giving output: "YES" for above case. Is the checker solution ignoring the ceil function mentioned in the question?
If you optimize for 7 days it will take 88/(7+1)+7=18 days.
Sorry I missed it. Thanks for clarification.
take x=9
Also for 8 days it would be 8 + ceil(88 / (8 + 1)) = 8 + 10 = 18
Please explain DP approach for C?
You can count how many arrays start with $$$i$$$, are length $$$j$$$, and are non-decreasing by using
and how many arrays start with $i$, are length $$$j$$$, and are non-increasing by using
The answer is then
dp state could be dp[i][j] , i the curent position in the array we are placing integers on, j curent difference between the numbers on i-1 position
I'm getting
Illegal Contest IDwhen I try to hack any solution.Go to submissions tab of the user and hack from there by opening the link (and not the popup).
code problem C:
cout << C(n + 2 * m — 1, n — 1);
How you arrived at this solution?
If you reverse the array A and append it to the back of B, then the sequence is decreasing (cause b[0]>=b[1]>=b[2]>=....>=b[m-1]>=a[m-1]>=a[m-2]>=...>=a[0]). Hence you need to find the number of decreasing sequences of length 2*m. Let x1,x2,x3,..,xn be the number of times 1,2,3...n have occurred. Then the number of solutions of x1+x2+x3+...+xn=2*m is the required answer (cause the order is fixed after choosing).
Wow, that's the most elegant approach! Thanks.
My solution was precisely the same. Here is (main part of) my actual solution:
Please explain your idea.
I spent more than an hour in C because 3rd sample test itself was failing. Later on realised that I had written mod = 100000007 instead of 1000000007. So didnt get time to solve problem D.
It might be convenient to use
1e9 + 7when modulo =1000000007, as it's both easier to read and less prone to mistakes :)EDIT: now with a (actually) working min-cost flow :Dd 69056043
We solve the problem with min-cost flow. For every edge $$$(i, j)$$$, add an edge from $$$i$$$ to $$$j$$$ with capacity $$$1$$$ and cost $$$b$$$, and an edge from $$$j$$$ to $$$i$$$ with capacity $$$1$$$ and cost $$$r$$$. No min-cost flow will contain both edges. If the edge from i to j is used, we say the edge is BLUE. If the edge from j to i is used, we say the edge is RED. Otherwise the edge is colorless.
A blue vertex having strictly more blue adjacent edges corresponds to it having strictly more in-flow than out-flow (if it is in the right partition), and strictly more out-flow than in-flow (if it is in the left partition). The same reversed holds for red vertices, and colorless vertices have no requirements.
For every blue node in the right partition and red node in the left partition, add an edge from the source to it with cost $$$-H$$$ (for some very large integer $$$H$$$) and capacity $$$1$$$, and an edge with cost 0 and capacity $$$\infty$$$.
For every blue node in the left partition and red node in the right partition, add an edge from that node to the sink with cost $$$-H$$$ and capacity $$$1$$$, and an edge with cost $$$0$$$ and capacity $$$\infty$$$.
Say the minimum cost circulation has value $$$V$$$, and $$$R$$$ is the cost of the optimal solution to the problem. Then if the problem is solvable, $$$V + kH = R$$$, and otherwise $$$V + kH \geq H$$$ (as we were not able to satisfy all of the requirements).
Hey in the function minCostCirc() shouldn't the line: if (edges[ei].ru & h) res += incEdge(ei, h);
be changed to: if (edges[ei].ru & h) res += (h*incEdge(ei, h));?
(Since the new cost = previous cost + (flow added * cost of the negative cycle ).)
Well spotted. Turns out that in every problem I tested my code on, either the cost didn't matter (only the flow along each edge in an optimal flow did) or the capacity of every edge with nonzero cost was 1 :Dd
I submitted the fixed code to min-cost max-flow on kattis, so it should definitely now work.
Which is the math explanation for A
AM>=GM, https://mirror.codeforces.com/blog/entry/73061?#comment-573250
My solution for A is a bit different. Its enough to check on just x = (n/2),(n/2 + 1), and (n/2 — 1). Its because I think in the optimal solution both terms on the LHS in x + d/(x+1) = n (in worst case) should be equal or close enough. This means x = n/2 or around that.
Can anybody hack this?
i also did it this way
It's not correct. Function f(x)=n/(x+1)+x has the smallest value in point sqrt(n)-1
Then n/(x+1)+x will be equal 2*sqrt(n)
You need to notice that he said $$$\dfrac{n}{2}$$$ and not $$$\dfrac{d}{2}$$$.
Its not possible to hack this, because it is always correct.
Proof: We need $$$x + \lceil \dfrac{d}{x+1} \rceil <= n$$$. Since $$$ \lceil \dfrac{d}{x+1} \rceil <= \dfrac{d}{x+1} + 1$$$, we try to solve $$$x + \dfrac{d}{x+1} + 1 <= n$$$.
$$$ y + \dfrac{d}{y} <= n $$$,
$$$ y^2 - n*y + d <= 0 $$$
$$$ ( y - a ) ( y - b ) <= 0 $$$, which means $$$y$$$ must be between both roots, so that we get negative sign.
i.e. $$$x+1$$$ should be between both roots. Also, both roots are centered around $$$\dfrac{n}{2}$$$, so this will always be true, if you take few possibilities around $$$\dfrac{n}{2}$$$ for values of $$$x$$$.
what if i just check for n/2 will it always be true
What's the intended solution for 1288F - Red-Blue Graph?
can anyone give me a tricky case for A?? I would like to see if my code is OK
What is the meaning of
non-ascending? Isn't the array $$$[1, 2, 5, 4]$$$ non-ascending because, well, it is not ascending?It says "sorted in non-ascending order" not just "non-ascending".
Well, when they say sorted in some order, the ordering is often clear. For example, if they say sorted in alphabetical, lexicographic, ascending or descending, it is known what they mean or even then in some cases, they explicitly define the ordering.
What kind of ordering does non-descending or non-ascending establish?
I understand from here that it is fairly obvious to everyone who got an AC and even to several others, but it wasn't obvious to me. I just feel it should have been defined for the benefit of participants.
A quick Google search found the definitions of these terms but only in the context of the ambiguities that arise out of using them :)
I hope that contest setters will define their terms in upcoming contests.
Anyway, I feel that despite this I stumbled upon an interesting problem. How would you approach problem C if
non-descendingis to be interpreted as not descending andnon-ascendingas not ascending.For example, if $$$[1, 2, 3, 4]$$$ and $$$[3, 2, 1, 5]$$$ are non-descending (say).
I spent the entirety of the contest and much later trying to solve this but couldn't. Any ideas?
I understand the term "sorted ascending" as every element is bigger than the previous one, and "sorted non descending" as every element is not smaller that the previous one.
But basically it is the same, it works to simply see both as one and the same.
For solving the new question that you have raised,
We need to find number of arrays $$$(a,b)$$$ such that $$$a$$$ is not descending ($$$ND$$$) and $$$b$$$ is not ascending ($$$NA$$$).
Simple inclusion exclusion gives,
number of ways $$$(a,ND,b,NA)$$$ = $$$all(a.b)$$$ — $$$(a,D)$$$ — $$$(b,A)$$$ + $$$(a,D,b,A)$$$
$$$(a,D)$$$ denotes $$$a$$$ is descending. ( note $$$b$$$ can be anything here ).
$$$(a,D,b,A)$$$ denotes $$$a$$$ is descending AND $$$b$$$ is ascending.
Now, $$$all(a,b)$$$ is straightforward. So is $$$(a,D)$$$ and $$$(b,A)$$$. And, for $$$(a,D,b,A)$$$ we can use the method that was required to solve Original $$$C$$$ of the contest.
How would you solve $$$(a, D)$$$? This is precisely where I was stuck.
$$$(a,D)$$$ is number of ways of choosing array $$$a$$$ of length $$$m$$$ with values between $$$1$$$ and $$$n$$$, such that it's elements are in descending order, ( and $$$b$$$ can be anything, so we must multiply a factor of $$$n^{m}$$$ ).
Now, number of descending depends a lot on your exact definition of "descending". Is it "strictly descending"? Is $$$[5,3,3,2,2]$$$ descending?
If you want only strictly descending, then you just need $$$m$$$ distinct values ( because "strictly" forces no repitition of values ). So final $$$(a,D)$$$ will be $$$ choose(n,m) * n^{m} $$$. ( $$$choose(n,m)$$$ chooses $$$m$$$ distinct values from $$$n$$$ possible values, and there is only one "strictly descending" ordering of these $$$m$$$ chosen values. )
If your definition of descending array allows equal values, then we have the following equation to solve:
$$$x_n + x_{n-1} + x_{n-2} + .... + x_3 + x_2 + x_1 = m$$$
$$$x_{i}$$$ denotes number of $$$i$$$s that we take in our array. We must find all non negative ( $$$x_i >= 0$$$ ) solutions of the equation, which is given by $$$choose(n+m-1,n-1)$$$. You can read more about Stars and Bars.
So, answer in this case would be, $$$(a,D) = choose(n+m-1,n-1)*n^{m}$$$.
$$$b$$$ cannot be anything. $$$a_i <= b_i$$$ for all $$$i$$$ has to still hold for the inclusion-exclusion calculation to hold. P.S. Thanks for the link.
This can be done with dp, instead of formuales directly. ( Maybe it could be done with formulaes, but I can't think of it ).
Let $$$dp[i][j]$$$ be number of ways to choose both $$$a[i]$$$ and $$$b[i]$$$ with $$$a[i] = j$$$
So, we must use $$$dp[i-1][x]$$$ where $$$ x >= j $$$ to make this result, and when $$$a[i]=j$$$, $$$b[i]$$$ can take $$$n-j+1$$$ values ( $$$j, j+1, j+2, ... n$$$ ). ( Note, $$$b[i]$$$'s are independent of each other ).
In problem A test case 22 inputs are
63243 999950885
The judge says the answer is No but if he works 31620 days on optimizing, his program will work in 31623 days and will fit the limit.
Am i doing somrthing wrong? awoo
Nevermind I was wrong :| Sorry.
Can anybody suggest easier or similar problem , based on same concept like D?
1185F - Two Pizzas uses a similar bitmask concept.
My rating hasn't changed after this contest and also this contest is not appearing in myProfile-> contests list. Can anybody explain?
Due to some reasons, Codeforces hasn't updated ratings for everyone yet. We just have to wait for a little longer.
For me, the wait is worth it! :D
How to solve c if both arrays are non decreasing?
The only thing I came up with is the following. Let $$$dp[i][j][k]$$$ be the number of such arrays of size $$$i$$$ with $$$j$$$ and $$$k$$$ being the last elements of $$$a$$$ and $$$b$$$ respectively. Then $$$dp[i][j][k] = \Sigma dp[i-1][x][y]$$$ for all $$$1 \leq x \leq j$$$ and $$$1 \leq y \leq k$$$. We can maintain these sums using prefix sums. The total runtime will be $$$O(mn^2)$$$.
Why the rating hasn't changed?There is always change in two hours,but now is after the open hacking about five hours?
Can't wait so long to become Master :/
Does anyone know when the system testing starts?
The system testing seems to be ended!
System testing is finished :D
EDitorial Please of Educational Round 80
Soo... Is it ratted?
yep, I had the same question. Too long :(
Are the ratings even going to update??
To be honest, I haven't met such situation. So who can tell me what's the matter with codeforces?
Waiting for 4 hours already !!
Is there a better way to do A other than binary search?
I tried binary search but it fails on test 50.
Yes, here's a $$$O(1)$$$ solution. $$$x + \lceil \dfrac{d}{x + 1} \rceil \leq n \iff \lceil \dfrac{d}{x + 1} \rceil \leq n - x \iff d \leq (n - x)(x + 1) \iff x^2 + (1-n)x + (d-n) \leq 0.$$$ This inequality has solutions in real nonnegative numbers if and only if $$$(n - 1)^2 \geq 4(d - n)$$$. Actually, working under assumptions of the problem, it has nonnegative integer solutions if and only if it has nonnegative real solutions, so we just need to check the inequality $$$(n - 1)^2 \geq 4(d - n)$$$ to obtain the answer. https://mirror.codeforces.com/contest/1288/submission/68780664
choose x to be n/2 or (n + 1) / 2
should be sqrt(x) or sqrt(x)+1, and just to be save, better check all x from sqrt(x)-3 to sqrt(x)+3 for optimal value.
okay,i just check sqrt(x) and accept
How on earth happens with codeforces rating calculating system?
When the new ratings will be available? Can anyone tell that?
Why is the rating changes not published even after 6 hours of completion of open hack phase?
During and after the contest there were no signs of any issues with the tests or whatsoever, so we should keep our faith strong.
1288A - Deadline can be solved using the first derivative of f (x) = x + d / (x + 1) because when this is 0 it is because this point is a minimum, here we see the third case of the example: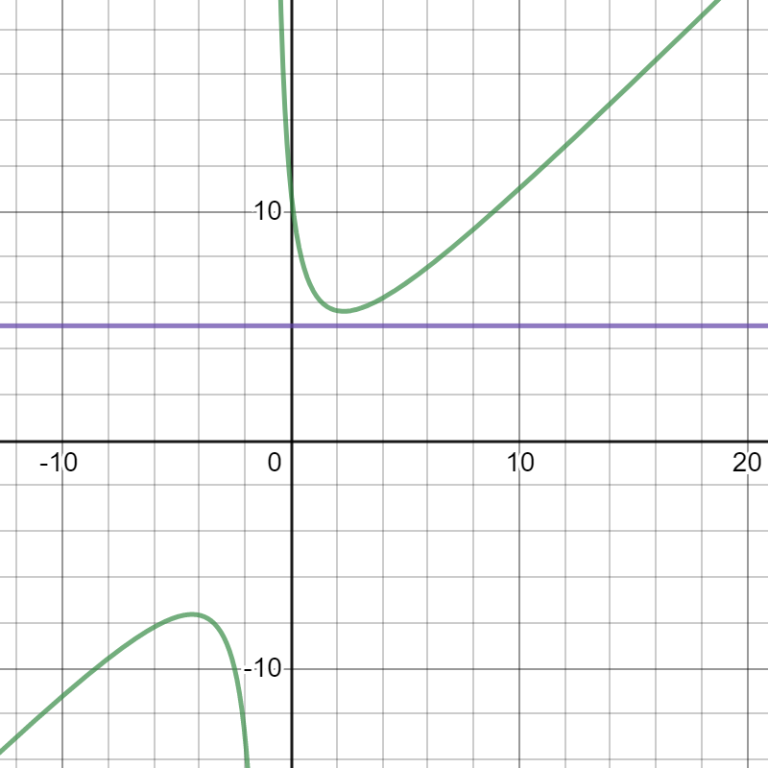 the derivative gives us: 1 — d / (x + 1) ^ 2 and if we equal it to zero it gives us x = sqrt (d) — 1, if we substitute this in the original function it results in (2 * d — sqrt ( d)) / sqrt (d), if this value is less than n then we print "YES" or else "NO". My submission is 68818558
the derivative gives us: 1 — d / (x + 1) ^ 2 and if we equal it to zero it gives us x = sqrt (d) — 1, if we substitute this in the original function it results in (2 * d — sqrt ( d)) / sqrt (d), if this value is less than n then we print "YES" or else "NO". My submission is 68818558
what is wrong in codeforces system?
I'm also waiting. It's too hard.
Maybe Mike had been busy fixing Codeforces SSL Certificate issue. Looks like its fixed now.
Yes Its fixed
It has been more than 6 hours until open hacking finished. System testing didn't even start yet! I feel like codeforces is having a problem with something!
The system testing actually finished at about 7 hours ago! <D
Why didn't the rates changed till now?
Before rating changes, there is system testing. So all the hacks would be added to the main tests. System testing didn't even start!!
Actually, it has already finished several hours ago.
meanwhile we could check our ratings here https://cf-predictor-frontend.herokuapp.com/
You are absolutely correct! But those ratings are not accurate. Some people may fail system testing! Lets hope that codeforces starts system testing very soon.
There was systesting
Oh, my bad. I didn't realize that! Thanks for informing me!
system testing is done ig
yeah you've got a point ,lets hope they start system testing soon enough
System Testing is finished I got a wrong answer on D and it was Ac yesterday ! But idk why the rating didn't update yet .
Me too. Added a +7 to my infinity and i got accepted. Feels bad man.
Sorry for u :( I start my for loop from 0 instead of 1 to get AC .. But the good thing i solved it afer the contest(it is not rated for me) :D
But sometimes its prediction is a little bit wrong.
when will be the rating updated
Isn't it already too late for results?
when will rating changes come out ?
At least, someone please tell the reasons behind the delay.
When it will be rated ?
now
My rating has been updated!
Finally, ratings got updated!
can some one explain how to solve problem E . I have knowledge of segment trees and BIT . But i have not solved much problem on them .
Refer this comment for the solution approach of Problem E
If you know basic segment tree but do not know how to find range distinct queries, then you can see the accepted answer of this stackoverflow question. Its explained in very easy to understand language.
old submission wrong on test case 50 which was Input
2
63242 999919263
63242 999919264
Participant's output
YES
YES
Jury's answer
NO
NO
new submission
this i used long double which solved the error
can anyone tell me why.
the ranges were 1<a,b<10^9 for which i think float would have worked fine
Editorials?
Auto comment: topic has been updated by awoo (previous revision, new revision, compare).
Will we get to know who won the prize?
I got invited eventually!
Please attach the announcement and editorial to the questions.