Hi everyone!
It's been a while since I posted anything. Today I'd like to talk about problem I from Oleksandr Kulkov Contest 2. Well, on some similar problem. Problem goes as follows: There is a rational number $$$x=\frac{p}{q}$$$, and you know that $$$1 \leq p, q \leq C$$$. You want to recover $$$p$$$ and $$$q$$$ but you only know number $$$r$$$ such that $$$r \equiv pq^{-1} \pmod{m}$$$ where $$$m > C^2$$$. In original problem $$$m$$$ was not fixed, instead you were allowed to query remainders $$$r_1,\dots,r_k$$$ of $$$x$$$ modulo several numbers $$$m_1,\dots,m_k$$$, which implied Chinese remainder theorem.
To solve this problem let's start with the observation that we always can recover answer uniquely. Indeed, assume that there are numbers $$$p'$$$ and $$$q'$$$ such that $$$1 \leq p',q' \leq C$$$ and $$$p'q'^{-1} \equiv r \pmod{m}$$$. That would mean that $$$pq'\equiv p'q \pmod{m}$$$. But initial constraints claim that $$$C^2 < m$$$, thus this equation holds in integers as well, so $$$\frac{p}{q}=\frac{p'}{q'}$$$. There are two major ways to approach this problem now, one associated with Euclidean algorithm and the other associated with continued fractions.
Euclidean algorithm. Now since we know that any $$$p,q$$$ such that $$$1 \leq p, q \leq C$$$ and $$$pq^{-1} \equiv r \pmod{m}$$$ would provide a solution, we can find some particular one by solving the following optimization problem:
To solve it we should look on how $$$q, 2q, 3q, \dots$$$ sequence behaves modulo $$$m$$$. We may see that it actually can be split into several arithmetic progressions with step $$$q$$$: we increase current number until it's not less than $$$m$$$, that is $$$k_1 q \geq m$$$. At this point we subtract $$$m$$$ from this number and obtain number $$$k_1 q - m$$$. Since this number is not greater than $$$q$$$ (otherwise we'd subtract $$$m$$$ on the previous step) we may say that this number is equal to $$$q'\equiv -m \pmod{q}$$$. Next time we subtract $$$m$$$ happens when $$$k_2 q \geq 2m$$$ and we obtain $$$k_2 q - 2m$$$, which is same as $$$2q' \equiv -2m \pmod q$$$. Let's draw $$$kq$$$ on the grid where $$$y$$$ axis stands for $$$\lfloor \frac{kq}{m}\rfloor$$$ and $$$x$$$ axis stands for $$$kq \pmod m$$$:
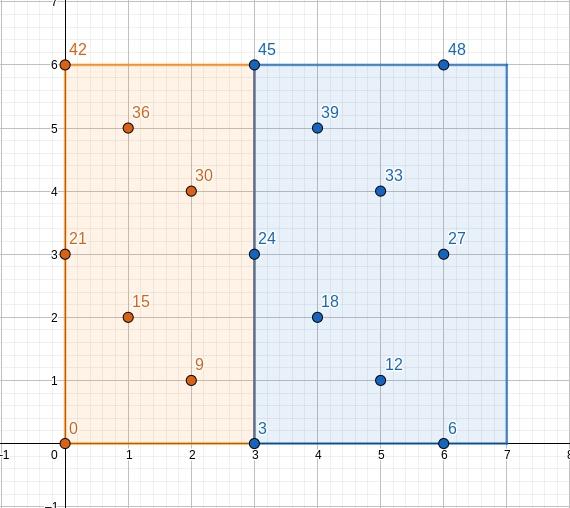
You can clearly see that while the main progression has a step $$$3$$$ modulo $$$7$$$, there is also a progression of starting points with step $$$-1$$$ modulo $$$3$$$. Since we look for the minimum element, we're only interested in starting points, thus we reduced the problem to this:
Wow, it looks like $$$q$$$ and $$$m$$$ just swapped and we now may deal with $$$m \pmod{q}$$$ as in Euclidean algorithm! Right? Err, not exactly. We switched from $$$(m,r)$$$ pair to $$$(r, -m \bmod r)$$$, while in Euclidean algorithm transition is to $$$(r, m \bmod r)$$$. And this is the problem here, as $$$(r, -m \bmod r)$$$ transition can't always guarantee logarithmic amount of steps. Thus, we need to make $$$(r, m \bmod r)$$$ transition. Luckily it turns out to be pretty simple as instead of minimizing problem we can solve maximizing problem:
And then return the result subtracted from $$$q$$$. This makes proper transition and the maximization problem may be reduced to the minimization one in the similar manner. In the end it all may be written in a pretty short code piece:
int min_rem(int m, int r, int c) {
if(c < 1) {
return inf;
} else if(r == 0) {
return 0;
} else {
int step = m % r;
int mx = c * r / m;
int t = max_rem(r, step, mx);
return r - t;
}
}
int max_rem(int m, int r, int c) {
if(r == 0 || c <= m / r) {
return r * c;
} else {
int step = m % r;
int mx = (c + 1) * r / m;
int t = min_rem(r, step, mx);
return m - t;
}
}
Continued fractions. We have to find the solution of $$$rq - p = km$$$ with $$$p,q \leq C$$$. Let's look on continued fraction for $$$\frac{r}{m}$$$ and its convergents $$$\frac{p_1}{q_1}, \frac{p_2}{q_2}, \dots, \frac{p_n}{q_n}$$$. It's known from continued fraction theory that if $$$\left|\frac{r}{m}-\frac{P}{Q}\right| < \frac{1}{2Q^2}$$$ then $$$\frac{P}{Q}$$$ is one of convergents for $$$\frac{r}{m}$$$. If we rewrite this inequality, we would obtain something more familiar:
In our case we know that there are $$$p,q$$$ such that $$$q \leq C$$$ and $$$rq - km = p \leq C < \frac{m}{C} \leq \frac{m}{q}$$$. Thus if we strengthen the constraint to be $$$m > 2C^2$$$ it would be safe to assume that $$$q$$$ is always the denominator of some $$$\frac{r}{m}$$$ convergent! Note that here $$$m > 2C^2$$$ bound matters, as there are $$$p,q$$$ pairs for which you won't find solution restricting to $$$m>C^2$$$ only, so this solution is less generic.
The solution here is a bit sketchy as I only heard some continued fraction solution in Petrozavodsk and tried to recover it here using basic facts about continued fractions from Wikipedia, sorry for that. There may also be $$$M > C^2$$$ solution for this case, but I couldn't figure it out.
P.S. I'd like to write some comprehensive article about continued fractions, but I need to solve some problems on it first. I would highly appreciate if you suggest some of those in the comments! Also feel free to share if you have any other solutions to this problem.
UPD: Very similar problem was also set by dreamoon_love_AA: link.











By the way, there is another Euclid-like idea that may be utilized to count the number of lattice points under arbitrary $$$kx+b$$$ line, which is kind of same as counting $$$\sum\limits_{k=0}^c (kr + b\bmod m)$$$, I once described it in this cp-algorithms article.
Very good read. I came across a similar article a few months back but cannot recall. I'd share the link once I find it (hopefully). Thanks for this :)
This article?
If I'm not wrong, Shoup showed a similar algorithm called "Rational reconstruction" in A Computational Introduction to Number Theory and Algebra.