When Centroid Decomposition comes?
- Suppose a problem says that how many paths have a length exactly k in a tree.
- Or, how many paths have xor k.
- Sum of all xor path in a tree.
- update a node Black to white or white to black. now query the shortest path from a node to a white node. etc.
So, it is clear, when a paths problem comes then we can use Centroid Decomposition.
For a single node query or from a specific node, DSU on Tree may do it.
Algorithm:
1. Find a centroid of current tree T.
What is Centroid?
Simply Centroid is a node if we delete it. It makes some subtrees where every subtree size must be less than sz/2 { sz is the size of the current tree T.}
How can we find it?
=> Take a node random node of current tree T. Now if it's every subtree size less than sz/2. Then it is a centroid. => If not, go to the highest size of the subtree.
Note: In a tree only two Centroid possible From Jordan Theorem. If there are two centroids. you can take any. Cause those two centroids to look like the same
=> Same thing must be done.
In this graph. If we start from node 1. Then Size[2]=7 which is larger than 11/2. so 1 is not centroid. Go to the 2. Now every subtree size less than 11/2. So for this graph centroid is 2.
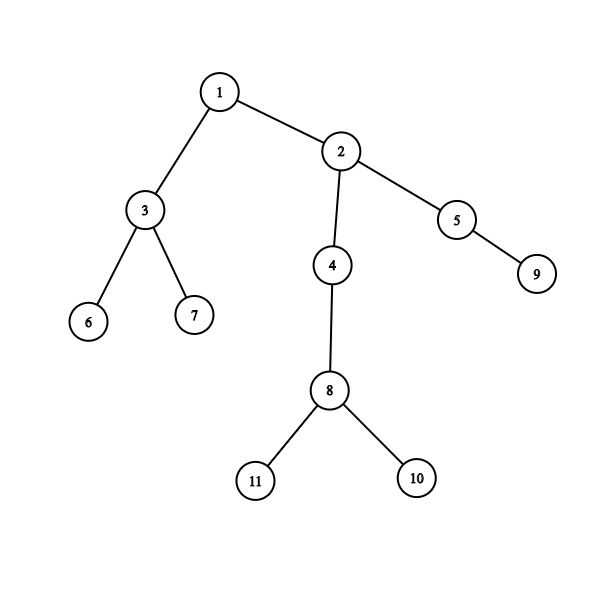
Here is the code for finding the centroid of the current Tree.
/// 'u' will give us the centroid
int u = _u;
while (true) {
int nu = -1;
for (int v : e[u]) {
if (!tocheck[v] || v == p[u]) continue;
if (1 + size[v] > sz / 2) nu = v;
}
if (sz — 1 — size[u] > sz / 2 && p[u] != -1
&&tocheck[p[u]]) nu = p[u];
if (nu != -1) u = nu; else break;
}
/// tocheck array check whether this node is already done as a centroid of any tree or not
/// For size array you need just a dfs call
void dfs(int u) {
for (int v : e[u]) {
if (v == p[u]) continue;
p[v] = u;
dfs(v);
size[u] += 1 + size[v];
}
}
2. Problem-Solving part.
Before Deleting centroid. we must find the answer for the current Tree T.
**You must solve this part with O(sz) time**
suppose we need to find how many paths length equal k. Then we need to compute for current tree T.
**how many paths go through the centroid of T which length equal k?**
Take your time and think about it. If we call a dfs from the centroid node and find the length of all nodes from the centroid, then it will be easier for us.
void dfs2(int u,int p,int val,bool flag)
{
if(flag) cnt[val]++;
else cnt[val]--;
for(auto v : e[u])
{
if(tocheck[v] && v!=p)
{
dfs2(v,u,val+1,flag);
}
}
}
void solve(int u,int p,int val)
{
if(val>k) return ;
sol+=cnt[k-val];
for(auto v : e[u])
{
if(tocheck[v] && v!=p)
{
solve(v,u,val+1);
}
}
}
void func(int u,int par)
{
sol=0;
dfs2(u,par,0,1);
sol+=cnt[k];
for(auto X : e[u])
{
if(tocheck[X])
{
dfs2(X,u,1,0);
solve(X,u,1);
dfs2(X,u,1,1);
}
}
ans+=sol/2;
}
3. Delete the Centroid node C and find the new centroid of all subtrees.
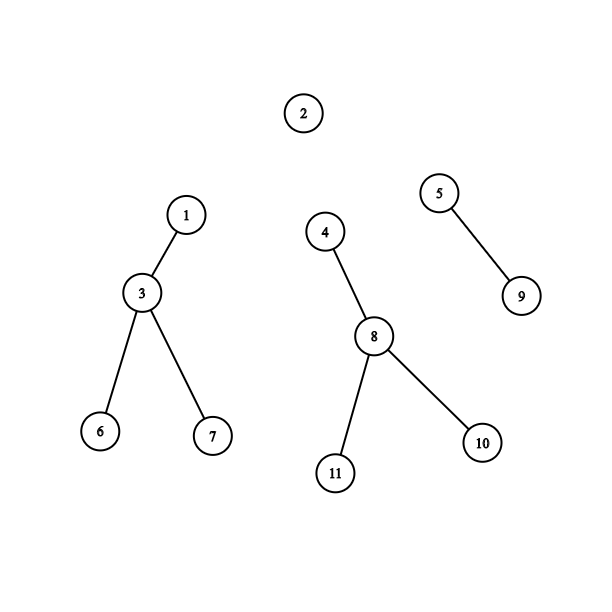
4. Repeat the same Thing from 1 to 3 for every subtree.
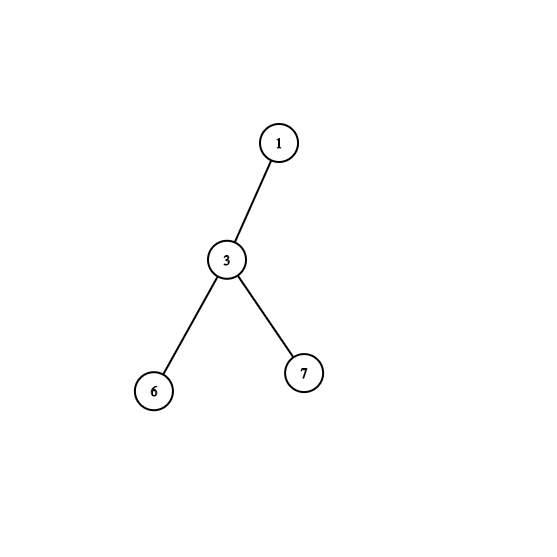
Property:
- The main property here is every node comes logn times under a centroid. So total complexity NlogN .
- Any path property like distance/xor/sum/etc. we can compute (logn+logn)times. Cause Highest depth for the centroid Tree is logn.
- LCA of any two nodes in centroid tree logn.
Full Code is here for finding all path length equal to k
#define ll long long
#define vi vector<int >
#define vil vector<ll >
#define pb push_back
#define fi first
#define sc second
#define pii pair<int , int >
const int N = 500050;
const int INF = 1e9+100;
ll sol,k,ans;
struct CentroidDecomposition {
/// cd for Centroid Tree
/// e for Main tree
vector<vi> cd, &e;
/// tocheck for checking a node is already in centroid tree or not?
vector<bool> tocheck;
/// p for tracking parent of a node
/// cnt for counting length
vi size, p,cnt;
/// centroid Tree root
int root;
CentroidDecomposition(vector<vi> &tree) : e(tree) {
int sz = e.size();
tocheck.assign(sz, true);
col.assign(sz, false);
cd.assign(sz, vi());
p.assign(sz, -1);
cnt.assign(N, 0);
size.assign(sz, 0);
dfs(0);
root = decompose(0, sz,-1);
}
void dfs(int u) {
for (int v : e[u]) {
if (v == p[u]) continue;
p[v] = u;
dfs(v);
size[u] += 1 + size[v];
}
}
/// we can solve it for any amount of k
void dfs2(int u,int p,int val,bool flag)
{
if(flag) cnt[val]++;
else cnt[val]--;
for(auto v : e[u])
{
if(tocheck[v] && v!=p)
{
dfs2(v,u,val+1,flag);
}
}
}
void solve(int u,int p,int val)
{
if(val>k) return ;
sol+=cnt[k-val];
for(auto v : e[u])
{
if(tocheck[v] && v!=p)
{
solve(v,u,val+1);
}
}
}
/// finiding centroid and get answer for this centroid
int decompose(int _u, int sz,int par) {
int u = _u;
while (true) {
int nu = -1;
for (int v : e[u]) {
if (!tocheck[v] || v == p[u]) continue;
if (1 + size[v] > sz / 2) nu = v;
}
if (sz - 1 - size[u] > sz / 2 && p[u] != -1
&&tocheck[p[u]]) nu = p[u];
if (nu != -1) u = nu; else break;
}
for (int v = p[u]; v != -1 && tocheck[v]; v = p[v])
size[v] -= 1 + size[u];
sol=0;
dfs2(u,par,0,1);
sol+=cnt[k];
for(auto X : e[u])
{
if(tocheck[X])
{
dfs2(X,u,1,0);
solve(X,u,1);
dfs2(X,u,1,1);
}
}
ans+=sol/2;
dfs2(u,par,0,0);
tocheck[u] = false;
for (int v : e[u]) {
if (!tocheck[v]) continue;
int V2 = 1 + size[v];
if (v == p[u]) V2 = sz - 1 - size[u];
cd[u].push_back(decompose(v, V2,u));
}
return u;
}
};
int main(){
int n;
cin >> n>>k;
vector<vi> tree(n, vi());
for (int i = 0; i < n - 1; ++i) {
int a, b;
cin >> a >> b;
a--; b--;
tree[a].push_back(b);
tree[b].push_back(a);
}
CentroidDecomposition cd(tree);
cout<<ans<<endl;
return 0;
}
You can find different type of code here Path problem and normal centroid implementation
** More problem **
You can also check this blog
Centroid Decomposition of a Tree by Tanuj Khattar
Sorry for the bad grammatical issues.
Thank You











Thanks a lot it helps me.
There can be atmost 2 centroids in a tree. One example is a path of length 4.
Thank you. But we need to choose one. And two node must have same subtree size. edited
Are you fan of youtube channel Mo Vlogs? YoYo-YoYo.
No. just for fun. Nothing else
more problems for practice :)
321C - Ciel the Commander
150E - Freezing with Style
715C - Digit Tree
293E - Close Vertices
776F - Sherlock's bet to Moriarty
833D - Red-Black Cobweb
914E - Palindromes in a Tree
809E - Surprise me!
342E - Xenia and Tree
Count It
Thank you. Edited
In the problem you solved, each time you find a centroid, you traverse(dfs) its complete-subtree, to find the number of nodes at distance 'i' from the centroid , so is the total time complexity O(N*log(N)) ?
Yes. Cause every node visited at most logn time..
So for n node.. it takes nlogn :)
One more question. Say for each centroid-'x',I traverse its complete subtree,then I traverse all of its children's subtree and keep doing this until I reach the leaves. What will be the time complexity now !?
its nlogn,
ok lets take an example,,
suppose the tree is,
In this tree centroid is 2.. ->now we traverse whole tree for a specific answer,
->then delete 2 from tree.
-> now we got three subtree ,
now, if we take subtree which contain 1,3,6,7 node.. and we go through this process , we got 3 as a centroid.
now again we got three subtree 1 , 6 , 7. and we delete 3 from the tree.
so its clear every time we divide a tree = how many adjacent node a centroid have.. they must be smaller than sz/2 . so its easy to check the complexity.
if we thought about binary tree, ( cause binary tree creates highest compexity here and you can understand easily)
from 1 centroid we delete one node get two subtrees (2 centroid) ,, take complexity O(n)
from 2 centroid we delete two nodes get 4 subtrees ( 4 centroid) ,, take compexity O(n-1)
from 4 centroid we delete 4 nodes, get 8 subtrees (8 centroid) ,, take complexity O(n-3) // 3 nodes already deleted before this process start
from 8 -----> 16 subtrees----> 16 centroid----> complexity O(n-7) // 7 nodes deleted
so if we sum all we get = O(n) + O(n-1) + O(n-3) + O(n-7) + O(n-15)+....... == nlogn
if this is not a binary tree, this complexity will be less than nlogn..
I think you can understand it.
thank you
Doing centroid decomposition may result in completely another tree, and the paths count or their length in the centroid tree for the particular node can differ the paths count/lengths in the original tree. I just don't understand this part. Could you please share a bit more details about this?
If you draw a centroid tree for any tree, it may not look anything like the tree at all. Instead it is just a decomposition of the tree that has some different properties (like same LCAs, NlogN paths etc.). You can retain the general information about the nodes from the given tree and carry them to the decomposed tree, and with the given advantage of logN height, some queries can be answered fast.
So that means we should get and store this info (lengths, etc...) while building the centroid tree and not after it. Is that correct?
Yeah. While or before building the centroid tree.
what do mean by NlogN paths ?
So there are a total of N nodes on the centroid tree and the height of the centroid tree is about logN. Each node can go upwards at most logN times until they reach the root of the tree. Thus, there are N * logN different paths that only go upwards (here, we don't really need the nodes in the middle of the roads, just the 2 endpoints). The key feature of the centroid tree is that the road between any two nodes on the original tree contains the LCA of those 2 nodes on the centroid tree. In other words, if we travel from node a to node b on the original tree, we have to go through their LCA on the centroid tree, because, on the original tree, they belong to different components divided by their subtree's centroid. From this information, we can conclude that the road between any two nodes, for example a and b, on the original tree can be divided into two roads, a to LCA and LCA to b. Essentially, any road in the original tree can be divided into two roads from the set of upward roads from the centroid tree; this set has N log N roads.
what is size array ?
Subtree size. if we take 'i' as a root, size[i] represents the numbers of nodes in his tree. Simply size array represents subtree size.
can someone explain the problem finding all path length equal to k ? how actually we calculated k length path with centroid decomposition? i don't understand the code .
if u find any good explanation then please share it.
If you're still having trouble you can watch algorithms live video on centroid decomp — he talks about similar problem: https://www.youtube.com/watch?v=3pk02p1-weU
In short you have to iterate over subtrees, first you calculate the of paths of a given length in a subtree (you can do it with simple dfs and a global table), then you try to match paths of this subtree with paths of previously seen ones (so if you choose a patch of length x from this subtree you can match it with paths of lengths k-x from other subtress) — to do it you keep an aggregate table that aggregates the number of paths of all lengths from previously seen subtrees
my sol: 232875731
To Find centroid can't we just use simple dfs
CORRECT ME if i am wrong.
EDITED: YES, I am wrong i find the case. - create tree with following edge 1-2 2-3 3-4 4-5 3-6
according to above discussion my answer should be 2/4 but it will be 3 (^_^)