Here you can find the solutions for the problems from the past round. You can ask questions in the comments below.

A Div 2

If a_i divide a_j than a_i ≤ a_j. So the number which will divide every other number should be less than or equal to every other number, so the only possible candidate — it's the minimum in the array. So just check whether all elements are divisible by the minimal one.

B Div 2

Easy to see, that Ksusha is unable to complete her journey if there is a sequence of consecutive # with length more than k.

C Div 2 / A Div 1

The first observation — we don't care about the actual strings, all information we need — number of pairs {0,0}, {0,1}, {1,0}, {1,1}. Count that and then just follow the greedy algorithm, for the first player: try to get a index with {1,1} if there are some, than {1,0}, than {0,1} and than {0,0}.

For the second player similar strategy: first {1,1}, than {0,1}, than {1,0}, than {0,0}.

After that just compare who has more 1.

D Div 2 / B Div 1

Every path from the topleft cell to the bottomright cell contain exactly n + m - 1 cells. And all of the should be of different color. So n + m - 1 ≤ k. Due to the small constraints for k we may assume that bruteforce might work. The only optimization to get the correct solution is some canonization of the colors. So let's go over all of the cells in some order and color them but with following condition. If i > j, than color i appeared later than color j. If we bruteforce in such way we will have about 1 million different patterns for max case. Than just match them with already painted cells and calculate for each pattern how many different permutations of color we can apply to it.

E Div 2 / C Div 1

After reading the problem statement one can understand that all we need is to calculate the number of positive integer solutions of equation: (a + b + c)³ - a³ - b³ - c³ = n.

The key observation is: 3(a + b)(a + c)(b + c) = (a + b + c)³ - a³ - b³ - c³, after that simply calculate all divisors of and then first go over all x = a + b, such that 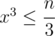then go over all y = (a + c) ≥ x, such that 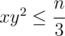and then determine z = (b + c), such that 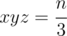. After that we need to solve the system a + b = x, a + c = y, b + c = z and find out how many solutions it adds.

D Div 1

We can see that we asked to calculate 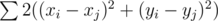for all integer points inside the polygon or on its border. We can see that we can process Xs and Ys independently.

For each x determine y_left, y_right, such that all points (x, y) where y_left ≤ y ≤ y_right are inside the polygon and the range [y_left, y_right] is as maximal as possible. Now let's assume that we have a₁, a₂, ..., a_k different points with fixed x coordinate (a₁ stands for x =  - 10⁶, a₂ for x =  - 10⁶ + 1 and so on).

Now the required answer is a₂a₁ + a₃(a₂ + 2²a₁) + a₄(a₃ + 2²a₂ + 3²a₁) + ...

We can see that:

(a₂ + 2²a₁) - a₁ = a₂ + 3a₁,

(a₃ + 2²a₂ + 3²a₁) - (a₂ + 2²a₁) = a₃ + 3a₂ + 5a₁,

and so on.

So we can precalculate partial sums like a₂ + 3a₁, a₃ + 3a₂ + 5a₁, a₄ + 3a₃ + 5a₂ + 7a₁ (the difference between two consecutive sums is 2(a_i + ... + a₁), so we can do that in O(k) time).

After this precomputation we just need to sum the results.

E Div 1

Let's assume that we have a data structure which can perform such operations as: — add point (x,y) to the structure;

• shift all points in the structure by vector (dx,dy);

• answer how many point (x,y) are in the structure where x ≤ x_bound, y ≤ y_bound;

• get all elements which are now in the structure;

For every vertex of the tree we will store the pointer to such structure.

How we update the structures. We will proceed all the vertices in dfs order, if we are in a leaf node, than we create structure which contains only one element (0,0).

Otherwise we will sort the children structures by it's size in decreasing order and assign the pointer of the biggest structure to the pointer of the current vertex (Don't forget to shift the structure by (1, weight of edge)).

After that we will go over all other children one by one and do the following thing:

• Shift the structure by (1, weight of edge);

• Get all elements from the structure;

• For every element (x,y) answer the query x_bound = L - x, y_bound = W - y (we use parent's structure);

• Add elements one by one into the structure;

After that answer the query x_bound = L, y_bound = W and add element (0,0).

The sum of the results of all the queries is our answer. It's easy to see that there will be no more than 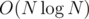queries and add operations.

The remaining part is designing the structure.

It can be done in many ways. One of the ways:

• We have small structures with sizes equals to powers of two;

• Each structure — it's two-dimensional segments tree;

• We can add one element in a following way: if there is no substructure with size 1, than add it; else get structures with sizes 1, 2, 4, ..., 2^k and all its' elements and rebuild the structure with size 2^k + 1;

• Shifting — just remember shifting vector for every substructure;

• Answering the query — go over all substructures and add the results.

Editorial was prepared by sdya and Seyaua