Problem A. Morning run
We were asked to find the expected value of meetings between the runners. How to do that? As the first step, expected value is lineal, so we can split the initial problems into the different ones: find the expected value of meetings between the fixed pair of runners. We will solve these problems. To do that we need to make some observations:
Let x be the distance between the two runners and they run face to face for infinite amount of time (probability of that obviously equals to 0.5·0.5 = 0.25). Then the first meeting will happen at time
 , the next one —
, the next one — 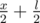 , the next —
, the next — 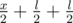 and so on.
and so on.Let us assume that every run ran for l time units. Then if two runners meet — they meet exactly two times. The probability of the meeting equals to 0.5, because in two cases they run in the same direction and in two cases in the different ones.
We will build our solution based on these two observations. As the first step let us represent t as t = k·l + p, where 0 ≤ p < l. Then each runner will run k full laps. What does that mean? Because we have 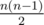 pairs of runners, then in those k laps each pair will have 2k meetings with probability equals to 0.5. So, we need to add
pairs of runners, then in those k laps each pair will have 2k meetings with probability equals to 0.5. So, we need to add 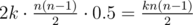 to the answer.
to the answer.
Now we need to take into account p seconds of running. Let us assume that the distance between two runners is x and they run towards each other. Then they will meet if 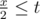 , or x ≤ 2t. They will meet once more if
, or x ≤ 2t. They will meet once more if 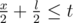 , ir x ≤ 2t - l. They cannot meet more than twice, because p < l.
, ir x ≤ 2t - l. They cannot meet more than twice, because p < l.
Let us fix one of the runners, then using binary search we can find all other runners at distance no more than x from the fixed one. Let us choose x as x = 2t, and then the number of runners at the distance no more than x stands for the number of runners which meet with the fixed one at least once. If x = 2t - l, we will find the number of runners which meet with the fixed one exactly two times. Multiplying these numbers by 0.25 — probability of the meeting, and add it to the answer.
The complexity of this solution is 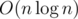 . We can reduce it using two pointers method.
. We can reduce it using two pointers method.
Problem B. Context Advertising
We were asked to find the maximal number of words we can fit into the block of size r × c. Let's first solve such problem: what is the maximal number of consecutive words which can fit in a row of lenth c, if the first word has index i. We can solve it using binary search or moving the pointer. Now let us build a graph, where vertices are the words and there is a directional edge between i and j, if words from i to j - 1 fit in one row of length c, but words from i to j don't. The weight of the edge is j - i. The we have the following problem: we need to find the path of length k, which has the maximal weight. Easy to solve it with complexity 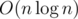 saving weights of all the paths with lengthes equal to the powers of two, or in O(n) time using dfs.
saving weights of all the paths with lengthes equal to the powers of two, or in O(n) time using dfs.
The other problems competitors faced — that we were asked to print the whole text, not only the length.
Problem C. Memory for Arrays
We were asked to find the maximal number of arrays we can fit into the memory. A small observation first, let the answer be k, then one of the optimal solutions fits the k smallest arrays into the memory. We can assume that we have arrays of size 1 and we want to arrange the memory for the maximal arrays as possible. Then if we have parts of memory of odd size, if we fit array of size 1 at this part we will obtain part of even size. From other hand, if we put arrays of bigger size we will not change the parity and if we don't fill it with arrays of size one and initially it's of odd size then in the end we will have at least one empty cell. So it's reasonable to put the arrays of size one into the memory of odd size. Let's do it until we can do it. We have three possible situations:
We don't have memory parts of odd size anymore.
We don't have arrays of size 1 anymore.
We don't have neither arrays of size 1 neither memory parts of size 1.
Let us start from the first case. Suppose that there are some arrays of size 1 left, but there are no memory parts of odd size. Easy to see then in such case we need to group arrays of size 1 in pairs and then consider them as the same array. So we can divide every number by two and reduce the problem to the initial one.
In the second case if we divide every number by two we will obtain the same problem (and that cannot increase the answer).
The third case is similar to the second one.
When implementing this we need to remember that first we have to fill the memory with arrays which are build from the maximal numbers of initial arrays.
The complexity of the given algorithm is 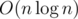 .
.
Problem D. Tennis Rackets
We were asked to find the number of obtuse triangles which satisfy the problem statement. Author's solution has complexity O(n2), but it has some optimizations, so it easily works under the TL.
Every triangle has only one obtuse angle. Due to symmetry reasons we can fix one of the sides and assume that obtuse angle is tangent to this side. Then we only need to find the number of such triangles and multiple the answer by 3.
Every side is also symmetric, so we can consider only one half of it and then multiple the answer by 2.
Let us assume that vertex A of the triangle has coordinates (0,0). Vertex B (0,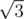 ) and C(2,0). Then we can find the coordinates of every single point at each of the sides and apply cosine theorem. We obtain the inequality which guarantee us that the triangle is obtuse. It can be written in many ways, on of them is following: If 1 ≤ i, j, k ≤ n — indices of points which are fixed at each of the sides, then triangle is obtuse iff: f(i, j, k) = 2i2 - i(n + 1) + 2j(n + 1) - ij - k(i + j) < 0. We can see that
) and C(2,0). Then we can find the coordinates of every single point at each of the sides and apply cosine theorem. We obtain the inequality which guarantee us that the triangle is obtuse. It can be written in many ways, on of them is following: If 1 ≤ i, j, k ≤ n — indices of points which are fixed at each of the sides, then triangle is obtuse iff: f(i, j, k) = 2i2 - i(n + 1) + 2j(n + 1) - ij - k(i + j) < 0. We can see that 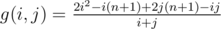 monotonically increases, so we can use moving pointer method applied to variable k. Then just go over all i from m + 1 to
monotonically increases, so we can use moving pointer method applied to variable k. Then just go over all i from m + 1 to 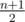 , then j from m + 1 till upper bound for k is less than or equal to n - m + 1 and just sum the results.
, then j from m + 1 till upper bound for k is less than or equal to n - m + 1 and just sum the results.
We should mention that all of the operations have to be done in int type, it significantly increases the speed.
Problem E. Sheep
Author's supposed greedy algorithm as a solution for this problem. Let us follow this algorithm. Let us create to label for every interval Positionv and MaximalPositionv.
Positionv — stands for position of v in the required permutation.
MaximalPositionv — stands for maximal possible position of v in the particular moment of the algorithm.
Also let's consider count as a counter with initial value of 0 and set of unprocessed vertices S. The algorithm is following.
Using binary search we find the maximal possible distance between the farthest sheep. And then check whether exists the permutation with maximal distance no more than K.
Sort all the intervals in the increasing order of ri.
Positioni = 0, 1 ≤ i ≤ n, MaximalPositioni = n, 1 ≤ i ≤ n, current = 1, count = 0.
Do count = count + 1, Positioncurrent = count, erase current from S, if S — is empty, required permutation has been found.
Look at every interval connected to current, and update MaximalPositionv = min(MaximalPositionv, Positioncurrent + K)
Build sets S(count, j) = {v|MaximalPositionv ≤ count + j}. If for every j ≥ K - count + 1 holds |S(count, j)| ≤ j go to the step 7, otherwise there is no such permutation.
Choose the minimal j such that |S(count, j)| = j. Choose from it the interval with the smallest ri and consider it as a new value for current, go to the step 4.
First let us discuss the complexity. Let us fix K (in total there are 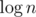 iterations with fixed K).
iterations with fixed K).
Every step from 4 to 7 will be done at most n times (every time size of S decreases by one). Every step can be implemented in O(n) time. The most difficult one — step 6. But we can see that it's not necessary to actually build the sets, all we need to know — their sizes. This can be done in linear time just counting the number of intervals that MaximalPositionv = i. Let if be Ci — then size of S(count, j) equals to C1 + C2 + ... + Ccount + j, which can be easily calculated with partial sums.
Now let us discuss why this algorithm works. If we have Position labels for every interval — we obviously have the solution. Now let us assume that we ended up earlier. Then we will show that there is no such permutation. If algorithm ended, it means that for some count (consider the smallest such count), exists j0, that |S(count, j0)| > j0 at this step. Then |S(count, k)| > k. Let us prove that from contradiction. From the definition of count we have |S(count - 1, j)| ≤ j for every j ≥ k - count + 2. Then |S(count, j)| = |S(count - 1, j + 1)| - 1 ≤ j for every j ≤ k - 1. And S(count, j) = S(count, k) for k ≤ j < n - count = |S(count, j)| = |S(count, k)| ≤ j. Finally |S(count, n - count)| = n - count. Then |S(count, j)| ≤ j for every j, so we obtain contradiction. That means if algorithm stops at step 6 we have |S(count, k)| > k. So exist at least k + 1 interval, which still don't have assigned label Position and they should be assigned after count. So one of the intervals in S(count, k) has to have the value of Position at least count + k + 1. But every intervals in S(count, k) connected to at least one interval with Position ≤ count. So, we obtain that there is now such permutation.










in E: why you just find the smallest ri as current? Can you explain it?
same question: why?
I have read your solution of problem E. There is a very big problem with the last part. You proved, that |S(Count, K)| > K. Okay. After that, you have a logic mistake: you're telling, that there is no way to end your permutation. Oh, yes, you're right! But you didn't prove, that there was no way to build the permutation in a different way with all conditions. Once again in another words: that's right, you have K+1 segments to put into K places, it's hard to make it. But you should prove, that in any other different beginning of the permutation (first Count positions of the array) there still will be some problems with ending it. And you didn't do it, cause these K+1 vertexes could be connected to the different vertexes before, could not be all connected to each other, etc... I couldn't really even prove that if there is a solution then there is a solution with the first segment with the smallest R_i.
P.S. Maybe I didn't get anything or someone has the right solution? I am trying to solve for a very long time... P.P.S The only condition for j in 6 statement is j >= 0, not what you have.
It's too old so nobody will prolly care, but the proof in editorial is just a copy of some lemmas in this paper. The paper contains a full proof. I tried to understand it, but it looks quite complicated.
Also the condition for $$$j$$$ is okay. You don't have to care cases about $$$MaximalPosition_i \le k$$$ because you can't make it. Of course, $$$j \geq 0$$$ is also correct.