All problems were developed by me Supermagzzz and Stepavly.
Author: MikeMirzayanov
Editorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
int main() {
int t;
cin >> t;
for (int test = 1; test <= t; test++) {
string b;
cin >> b;
string a = b.substr(0, 2);
for (int i = 3; i < b.size(); i += 2) {
a += b[i];
}
cout << a << endl;
}
return 0;
}
Авторы: Supermagzzz, Stepavly
Editorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
using ld = long double;
using ll = long long;
void solve() {
int n;
cin >> n;
int a = 0, b = 0;
for (int i = 0; i < n; i++) {
int x;
cin >> x;
if (x % 2 != i % 2) {
if (i % 2 == 0) {
a++;
} else {
b++;
}
}
}
if (a != b) {
cout << -1 << endl;
} else {
cout << a << endl;
}
}
int main() {
int n;
cin >> n;
while (n--) {
solve();
}
}
Авторы: Supermagzzz, Stepavly
Editorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
int main() {
int t;
cin >> t;
for (int test = 1; test <= t; test++) {
int n, k;
cin >> n >> k;
string s;
cin >> s;
int res = 0;
for (int i = 0; i < n;) {
int j = i + 1;
for (; j < n && s[j] != '1'; j++);
int left = s[i] == '1' ? k : 0;
int right = j < n && s[j] == '1' ? k : 0;
int len = j - i;
if (left == k) {
len--;
}
len -= left + right;
if (len > 0) {
res += (len + k) / (k + 1);
}
i = j;
}
cout << res << endl;
}
return 0;
}
1367D - Task On The Board Автор: MikeMirzayanov
Editorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
#define forn(i, n) for (int i = 0; i < int(n); i++)
int main() {
int q;
cin >> q;
forn(qq, q) {
string s;
cin >> s;
int n;
cin >> n;
vector<int> b(n);
forn(i, n)
cin >> b[i];
vector<vector<int>> groups;
while (true) {
vector<int> pos;
forn(i, n)
if (b[i] == 0)
pos.push_back(i);
if (pos.empty())
break;
groups.push_back(pos);
forn(i, n)
if (b[i] == 0)
b[i] = INT_MAX;
else
for (int pp: pos)
b[i] -= abs(i - pp);
}
map<char, int> cnts;
forn(i, s.size())
cnts[s[i]]++;
auto j = cnts.rbegin();
string t(n, '?');
for (auto g: groups) {
while (j->second < g.size())
j++;
for (int pp: g)
t[pp] = j->first;
j++;
}
cout << t << endl;
}
}
Автор: MikeMirzayanov
Editorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
int main() {
int test;
cin >> test;
while (test--) {
int n, k;
cin >> n >> k;
string s;
cin >> s;
vector<int> cnt(26);
for (char c : s) {
cnt[c - 'a']++;
}
for (int len = n; len >= 1; len--) {
vector<bool> used(len);
vector<int> cycles;
for (int i = 0; i < len; i++) {
if (used[i]) {
continue;
}
int j = (i + k) % len;
used[i] = true;
cycles.push_back(0);
cycles.back()++;
while (!used[j]) {
cycles.back()++;
used[j] = true;
j = (j + k) % len;
}
}
vector<int> cur_cnt(cnt);
sort(cycles.begin(), cycles.end());
sort(cur_cnt.begin(), cur_cnt.end());
bool can_fill = true;
while (!cycles.empty()) {
if (cur_cnt.back() < cycles.back()) {
can_fill = false;
break;
} else {
cur_cnt.back() -= cycles.back();
cycles.pop_back();
sort(cur_cnt.begin(), cur_cnt.end());
}
}
if (can_fill) {
cout << len << endl;
break;
}
}
}
}
1367F2 - Flying Sort (Hard Version)
Автор: MikeMirzayanov Stepavly Supermagzzz
Editorial
Tutorial is loading...
Solution
#include <bits/stdc++.h>
using namespace std;
using ld = long double;
using ll = long long;
void solve() {
int n;
cin >> n;
vector<int> v(n);
vector<pair<int, int>> a(n);
for (int i = 0; i < n; i++) {
cin >> v[i];
a[i] = {v[i], i};
}
sort(a.begin(), a.end());
vector<int> p(n);
int j = 0;
unordered_multiset<int> next;
for (int i = 0; i < n; i++) {
if (i > 0 && a[i].first != a[i - 1].first) {
j++;
}
p[a[i].second] = j;
next.insert(j);
}
unordered_map<int, int> d;
vector<int> dp1(n), dp2(n), dp3(n), cnt(n);
for (int i = 0; i < n; i++) {
if (next.count(p[i])) {
next.erase(next.find(p[i]));
}
if (d.count(p[i] - 1)) {
if (!d.count(p[i])) {
dp2[i] = max(dp2[i], dp1[d[p[i] - 1]] + 1);
if (!next.count(p[i] - 1)) {
dp2[i] = max(dp2[i], dp2[d[p[i] - 1]] + 1);
}
}
if (!next.count(p[i] - 1)) {
dp3[i] = max(dp3[i], dp2[d[p[i] - 1]] + 1);
}
dp3[i] = max(dp3[i], dp1[d[p[i] - 1]] + 1);
}
if (d.count(p[i])) {
dp3[i] = max(dp3[i], dp3[d[p[i]]] + 1);
dp2[i] = max(dp2[i], dp2[d[p[i]]] + 1);
dp1[i] = dp1[d[p[i]]] + 1;
} else {
dp1[i] = 1;
}
dp2[i] = max(dp2[i], dp1[i]);
dp3[i] = max(dp3[i], dp2[i]);
d[p[i]] = i;
}
cout << n - *max_element(dp3.begin(), dp3.end()) << "\n";
}
int main() {
int n;
cin >> n;
while (n--) {
solve();
}
}










Practice really helps you... After continuous practice my first contest where I solved A,B,C(yaa I know Div 3) but still it's a big achievement for me... Looking Forward to Global Round
I'm new here can anyone tell about CF Global Round... I mean is that different from Div1+2 round??
Well you solved ABC in Codeforces Round #644 (Div. 3) too
You sir just lied
That Day all the three problems had more than 11k submissions they were easy and that time I was not that serious about CP as I'm now...
But still I don't know why the sense of relief and satisfaction I got today was the best... It really felt good...
I felt like Lewis Hamilton in a Mercedes! Get in there Lewis!
I felt like Maldonado, getting wrong submissions here and there.
Video Tutorial for Problem A,B,C,D,E
Task D took soul out of me but never showed Accepted
You have 0 submissions in your profile right now. Probably you did not solve any question and still saying this (weird flex) or solved them from a second account. Either way, not healthy brother. Please refrain from doing this.
Hello guys! I'm new to codeforces and I enjoyed this div 3 contest even tho i only solved first 3 problems. Div 1 and 2 contests demotivated me..
can someone tell me is this contest was rated or unrated ?
It's rated.
Yes, it was rated for all the participants with a rating less than 1600 or are a new participant.
Can you tell why my ratings didn't change even though i have a lower rating?? Is it the case for anyone else too?
I had a look at your submissions for the contest. Apparently, you have been marked as "out of competition" (denoted by the asterisk above the username). I hope you followed the participation guidelines.
How to solve F2's last testcase for 16 operations?
Keep 5 5 9 9 and move the rest accordingly
C can be solved without handling cases separately.
append $$$100\ldots0$$$ at the beginning and $$$00\ldots 01$$$ at the end of the string ($$$k$$$ zeros in each sequence)
Give me five I appended k zeros at the beginning and k zeros plus 1 at the end. 83967055
I also did the same
How about handling no cases and doing using segment tree? xD
how will you use segment tree here?
83956065 here's how, though I've used BIT instead of segment tree.
.u can try this https://mirror.codeforces.com/contest/1367/submission/83999647 .
Another approach: You can iterate through the string and keep a count of zeros from the last '1'. If count becomes greater than k, increment ans by one and assign count = 0. If present element is '1' and count < k, decrement ans by one and assign count = 0. 84095691
You can actually solve problem c : social distancing in O(n) time complexity and O(1) space complexity like this :
The space complexity if $$$\mathcal{O}(n)$$$ , and not $$$\mathcal{O}(1)$$$, because you create the vector room. Here is my in-place solution:
can u explain the logic please?
This contest was almost DIV 2 ..... PS — Good problems
yep div3 is getting more and more difficult.
It felt like a Div 2 contest after C
You can do problem C using a simpler approach. Initialize ans = 1, count = 0. count stores the value of the present table with respect to the previous '1'. If count becomes greater than k then, place a person on the table, i.e. increment your ans by one and assign count = 0. If you come across a '1' and count <= k then that the previous person was wrongly placed on the table, so decrement ans by one and assign count = 0
Thanks alot this is very clever solution.
Here is the code: 84095691
Bro Your code gives wrong output for test case:
1
9 3
100100000
It gives 0 output whereas correct output is 1.
For this test case k = 3, whereas number of empty seats between the first and fourth seats is 2. The problem statement says it is guaranteed that the rules of the restaurant are satisfied for string s. So this test case is wrong.
How to do D but while preserving the order of characters from s in t.
I misread the question in contest, and actually tried solving this. The only solution I could come up with, was to generate all possible subsequences of size m from s, and check if b is valid for that string.
It can be optimized a bit as different values in b will correspond to different characters and vice versa so we can choose p(no of different values in b) alphabets and construct a string t accordingly and check if it is a subsequence of s. I could not optimize it any further.
But, different values won't necessarily correspond to different characters, for example take the following string.
t:
aacb:
[2, 1, 0]different values correspond to same character
In fact same values may correspond to different characters. Take the following example.
t:
cabb:
[0, 2, 2]Although, I think the following can be done. Try to solve this question too like the actual question, but instead of assigning the greatest character to indices containing zero, assign a number which will be used to store information whether characters
t[i] < t[j]ort[j] < t[i].abs(i - j)(where i is the current index containing unvisited zero) from them, and mark the current zero index as visited.The above algorithm is same as the solution to the original problem, but instead of assigning characters, we are assigning numbers.
Dry run for "cab":
1. b:
[0 2 2], visited:[F, F, F], ans:[-1, -1, -1]2. b:
[0 1 0], visited:[T, F, F], ans:[3, -1, -1]3. b:
[0 0 0], visited:[T, F, T], ans:[3, -1, 2]3. b:
[0 0 0], visited:[T, T, T], ans:[3, 1, 2]Now, in ans array if
ans[i] < ans[j], thent[i] < t[j]must be true. Therefore, we can use ans array to generate a valid subsequence from s, using backtracking.Although, I am not sure what will be the time complexity of the same.
Can someone please tell me what's wrong with my submission to C? https://mirror.codeforces.com/contest/1367/submission/83970779
The loop with the search with lower_bound is not ok. You check only the distance to the next 1, not to the previous one. And, you cannot only check every kth index, you would need to check each one.
Thanks I got it now.
For E, we may observe the following:
Suppose the length of the necklace is l. Then the necklace can be decomposed into l/gcd(l,k) consecutive portions of length gcd(l,k). These l/gcd(l,k) portions must be identical by the k-beautiful property. Now we store the frequencies of every letter, and check if sum over all letters, frequency[letter]/(l / gcd(l,k)) exceeds k. If so we have a necklace of length l, else there is no necklace of length l.
But why the gcd works here?
It felt more of a DIV 2.5 contest. btw good problems, enjoyed solving them.
Video Solution to C and D
please do make vedios of atleast e or f , this is div3 afterall.
Video for E
Please don't upload the videos just after contest. Do this at least 12 hours after contest is over. Some people will tend to watch your video immediately afer contest instead of upsolving. Thanks.
Why do you think you have to tell people what to do?
And why do you think i forced him to do anything? I just said my point in a manner of request. He is free to do anything what do he wants.
And people downvoting my comment are same which regularly post shitty things like-- I have been practising for 3 years and i am not improving-- instead of upsolving.
I think you also have an option of not watching the videos before 12 hours?
He is worried about those who don't improve even after practicing for 3 years. Haha
ur profile shows registered 4 months ago
No, you misread what i was saying.
I had a different approach for both E and F
1367E - Necklace Assembly , 84000671:
I created a count, c, of occurrences each letter, and then I iterated over each factor, f of k. Then I checked for the highest multiple of f that was a valid length using patterns of length f. For each multiple m * f, I took the sum of floor( c / m) for each count, and if the sum was >= f, it was valid.
1367F2 - Flying Sort (Hard Version) , 84030983
The main idea I used was that we would minimize the number of operations by finding the longest subarray of the sorted array that was also a subsequence of a . I kept a sorted map of numbers to a sorted list of indices the number appears at. Then I iterated through the map and kept track of the longest subarray found.
E -> how about taking top f elements in count, c, array and then take the least element l among them. then, ans=max(ans, f*l)
Your approach doesn't allow the same letter to be used more than once in the repeating pattern
say you had this test case:
Your counts would be 8, 4, and 1. The factors of 3 are just 1 and 3.
For 1, applying your approach would give us 8
For 3, applying your approach, the minimum is 1, giving us 3
The correct answer, however, would be pattern of aab repeated 4 times, which is a length of 12.
Check this solution. You could use gcd
Any proof why it is true " the longest subarray of the sorted array that was also a subsequence of a" ?
The elements that are not moved have to form a sorted subsequence. So if we can maximize the length the sorted subsequence, the number of operation is minimized.
Thanks.
Thanks for helping me find my mistake in E.Was doing everything correctly except for adding the floor of C/2 instead of the floor of C/M. It just slipped my mind and I was rotating all necklaces by half of their length and hence trying to find a palindrome, I needed to find if there can be M similar blocks instead of 2 similar blocks. Thanks once again.
can you please elaborate on keeping the track of the longest subarray . I don't think we can do that just iterating linearly .
That's true, I did gloss over that a bit. When I iterate from one unique number to the next largest, there are 2 possible cases
case 1: The last index in the previous number is less than the first index of the current number. Then we can just extend the subsequence and continue to the next number
case 2: case 1 is not true. In this case, we need to start a new sequence, but there's 3 things we need to look at.
a. We take the earliest index of the current number that is greater than the last index of the current number and add those number to the end of the current sequence.
b. We then also look for the longest sequence of just the previous and current numbers. For each index of the previous number, we find the earliest index of the current number that is after it, and we have a subsequence with just those indices.
c. We find the latest index of the previous number that is smaller than the first index of the current number and start our new subsequence with them.
submission link: 84023424
Thank you so much! Even though I didn't fully understand your explanation, it gives me some hints. Here's my c++ implementation 84279237 for those who are not familiar with kotlin (like me). The implementation is different but I believe the idea is the same.
Why greedy approach for distributing letters to cycles works in problem E? Because I think that in general it shouldn't work. Let's say we have buckets of size 6 and 10 and want to fill them with values 5, 5, 6. Then the best choice is to put two 5s in bucket of size 10 and 6 in bucket of size 6. Greedy approach doesn't work in this case. Does problem E satisfy some constrains that allow for greedy approach to work?
Because of the way to form the graph, all the cycles will have the same size, a graph of size n with edges between i and (i+m)%n, will have gcd(n,m) cycles of size n/gcd(n,m).
Thanks! I get it now
Thanks
How cycle size is exactly gcd(n,m)? Is there any proof of it?
Imagine that you have a number i, and you replace it with (i+m)%n in one operation, now, we will calculate the first time that this number will be equal to i again, we can show that we want to find the smallest k such that ( i + k * m ) = i ( mod n ), we can substract the i's and left k * m = 0 ( mod n ), so k = n / gcd( n , m ). and, if we start with each number after n / gcd( n , m ) we will find a cycle, that's why all cycles will be equal, and if each one has size n / gcd( n , m ), there will be gcd( n , m ) cycles.
Thanks a lot
In a necklace of length m, if you rotate by k, you notice that you require each subcycle (starting with any bead, and jumping k hops at a time) in the necklace to have same beads.
Now each sub-cycle will be produced by starting at i, and then after jumping k steps for x no. of times we will reach back at i. This completes our sub-cycle i.e. ($$$i + kx \equiv i mod m$$$) where x as you can see is the no. of jumps taken to reach back at i, also is the length of this sub-cycle.
Or, ($$$i + kx - my = i \implies kx = my$$$) for some integer y.
Now to find the min. x such that above equation holds, you see k and m are fixed, so kx = my = lcm(k, m). And as we know lcm(k, m) = km/gcd(k, m) = km/g.
Therefore, ($$$x = lcm(k, m)/k \implies x = km/kg \implies x = m/g$$$). Hence proved length, x of sub-cycle produced is size/gcd(size, k).
Now to prove that no. of subcycle will be gcd(k, m):
you can see that each sub-cycle will of equal size, starting with some i, j, ... , also each element has to be a part of exactly 1 such subcycle, thus product of no. of subcycles and size of each such subcycle must be 'm', hence the proof follows.
But what's it's proof?
Can someone help me with my code for Prob.C: Submission
see this test case :
7 1
1000001
Your solution gives the output as 1, but it should be 2 because we can place '1' at 3rd and 5th position.
https://mirror.codeforces.com/contest/1367/submission/84030518 pls can anyone tell y it is giving error in test case 54 of pretest 2 thnks in advance
In problem C for block that is neither first nor last,why cant we do (number of zeros in block)/ (2*k+1)
Check this https://mirror.codeforces.com/contest/1367/submission/84029802
can u tell error in mine? https://mirror.codeforces.com/contest/1367/submission/84030518
i was doing the same ... got WA!
I also explain solutions to these problems at the end of my screencast of the round if you would like a more visual explanation that what the excellent editorial here provides.
thank you
Can you give an elaborate explanation for the solution of question D? I did not understand it!:/
What part was confusing?
The idea is as follows:
Hello All, I have a question related to Social Distancing. Input: 6 2 000000 This input comes under the separate case mentioned in the editorial which is "a string consisting only of zeros". So we don't need to remove any zeros from the beginning or end. So answer should be floor(6/2) which is 3. But the correct answer as per the sample test case is 2. Can someone explain where I understood incorrectly? Thanks
It is not floor(n/k), but floor((n-1)/(k+1))+1
It's ceil(n/(k+1))
It's not related to the question you asked.
pk1993 , Why did your rating start from 0? My rating started from 1500. I started participating around 2 years ago. Is there any change in the codeforces initial rating system?
I believe I have a really nice solution (as well as clean) for the problem E -> 84022899
Looks like 84012097
lol i was looking for ways to solve E and found my own code
I don't understand the concept of GCD here...Please explain :)
I did this -
AC solution : 84033889
If you observe carefully, you will see there will be some cycles forming of same size. So we will check each size possible of the necklace. let's say we want to check if necklace size of x is possible or not. Let's say g = gcd(x, k). After g beards in the necklace, the letter has to be the same. So there will be g cycles. x sized necklace will consist g cycles of (x/g) size. Now we need to check if we can get g cycles of (x/g) size. This gcd idea can be a bit hazy, if you are finding it hard to understand, I will highly recommend you to draw some pictures and the thing... It really helps get a concept clearly :D And then let me know if you have further doubts. Happy Coding :D
I could not understand the tutorial of Problem F. Can somebody please elaborate a little more. Thanks in advance. I just want to understand the logic here. The implementation part is clear to me.
Let's say we have an array [3,10,10,1,3,7,7,0] . We can map it to [3,5,5,2,3,4,4,1] so the coding part become easier. Now let's sort it [1,2,3,3,4,4,5,5]. Now we need to find the longest sub-sequence in the original array, which is also a sub-array for the the sorted array (If you subtract it's length from n, you will get the answer) . You can see here a interesting fact that [3,5] or [2,3,4,4] can't be a answer because it is a sub-sequence for the original array but not a sub array for the original one. So it's clear that there there has to be body , prefix, suffix . Body has to contain all the all element fully (It means if there are 5 4's , it has to contain all the 5 4's.) and prefix would be the maximum you can take legally before body's first element (simply the amount of (body's first element)-1 equals element before the body starts) and suffix would be the maximum you can take after body's last element(simply the amount of (body's last element)+1 equals element after the body ends). This is the basic idea. But there is a case, you also need to focus on. You need to check all the possible sub-sequences containing only two different elements. I got AC doing this 84144777. Please let me know, if you have any further doubts. Happy Coding :D
nice problems
I never said we need to take the LIS. We need to take fulled connected increasing sub-sequence! In your case we if we sort the array, it would be [ 0 1 2 3 ] and the original array is [ 0 2 1 3 ]. We have take a the maximum sized subarray from the sorted array which also have to be a sub-sequence of the main array. We can't take [0 2 3] as it isn't a sub-array of the sorted array. We can take [0 1] or [2,3] ! Hope this helps you to clear the fact!
yup bro I got it just few seconds ago... Thanks Bro :P Farhan132
Anytime Bro!
Saw your code. Feels like you used priority_queue to store the no. of a[i]s present in the array by storing 1+p[a[i]].top() into p[a[i]]. Isn't it?
But, still didn't get how are we finding the length of the increasing subsequence in the original array(after coordinate-comp.) which is also the subarray in the sorted array? How are we doing this using priority_queues? I noticed you are taking the maximum of the b[i]s which is, of course, the size of each priority_queue. So ain't we only considering all the elements of the same type(all elements being equal to "x") as the only candidate for increasing subsequence(which is subarray when array gets sorted). Please help !!
If you look carefully in my code. I have not used priority queue! I just declared it as I was trying different methods. I tried 2-3 times with priority_queue before this and seems like implementing with it kinda impossible for me! To find the right sub-sequence, I am taking a number fully, (like if there is 3 1's, I will take all the three), then let's say before the first 1, there was 2 zeroes. So I will take them too. Now If all the 2's exists after the last 1, I will continue to the two and will take a prefix = ( 3 (one) + 2 (zero's before one) ). If not then I will take the number of 2 after the last 1 as suffix! And will move to two as 0 prefix. If get clear on this part, it would become really easy for you to do the rest!
I did F2 without dynamic programming.
Basic idea: The subsequence which should not be touched while making operations would have the set of numbers as $$$b_1, b_2 \ldots b_k$$$, where $$$b_1 < b_2 \ldots b_{k-1} < b_k$$$. And it must have complete segments for every number $$$b_2, b_3 \ldots b_{k-1}$$$, whereas it could have incomplete intervals for $$$b_1$$$ and $$$b_k$$$.
84032732
The part of idea is clear for me. Can you please explain a bit about the implementation? I am finding it hard to understand.
First case where I used deque(just for simple understanding, it's not even necessary) is the case when $$$k$$$ in the above sequence is greater than $$$2$$$. We can use sliding window for calculating it.
Next case, where I used a queue is when $$$k=2$$$, so both $$$b_1$$$ and $$$b_2$$$ are incomplete intervals.
I actually got a idea by myself and it took 5 WA to get the AC. Thanks a lot for the help and sorry I thought first to try my idea then yours.As It took me 28 hours to get AC, so I was late in reply.
What is the time complexity for this code ? (Question E ) , if |S| = 10 6
$$$ O(n\log n) $$$, because $$$cnt_j$$$ is bounded by $$$n/j$$$, so the whole thing grows at a rate of $$$H_n = O(n\log n)$$$. The added condition
k%cnt!=0will speed it up in some cases, but in the situation $$$k=1$$$ for example, it won't make a difference. It's hard to quantify how much it will affect the runtime in other cases, since it basically depends on the number of divisors of $$$k$$$ which are in the range $$$[1, n]$$$, as well as how "spread out" they are in that interval.I guess C can be solved in an easier approach and straight forward way.
Time complexity: O(N) Space complexity : O(1)
What's with this new trend of $$$\textbf{O(1)}$$$ space complexity ? And in your code you have read the whole string using,
That is clearly $$$\textbf{O(n)}$$$ space.
Supermagzzz In Question C instead of floor((number of zeros)/k) it should be ceil((number of zeros)/(k+1))
For those scratching their heads about F2 test case 3 #4999, try the following input (the correct answer is 2):
Checker for problem D was wrong during the contest. My submission was hacked and it now fails on test 1 (it didn't during the contest)
I think the testing was not appropriate for the 4th ques during the round ,during the round it showed to pass on first test case but after the round it was hacked on same test case (I did not pay attention to change the code as it was shown accepted and lost the score after the hack)
PROBLEM C without formulas and handling cases seperately---->
Simply use greedy approach and put one's from left to right if it satisfies the condition (i.e currentindex-previousindexhavingone > K)and increase the answer by 1 whenever in future your condition gets violated (might be due to subsequent one) you decrease the answer by 1.Here is the code -------->
There also exists an O(n) solution for C: 83977850
solved E without graphs.. just gcd and some basic operations: solution
Video tutorial for problem E
My approach for problem — C
We need to find number of unoccupied table which can be occupied so lets marks those table, or change s[i] = 0 to s[i] = x. Than count number of x in our final string x. Working iterate from 0 to strings length (n).
1)if s[i] is 0 than check the index of prev 1 or prev x in the string
2)if i — prev1 is > k marks this 0 as x and store this position (prev x).
3) if s[i] is 1 check for prev x.(which is already stored)
4) if i — prevx <= k change s[prevx] to 0
5) marks prev1 = i.
Submission Link — https://mirror.codeforces.com/contest/1367/submission/83973628
in the editorial of social distance i cannot understand the statement res += (len + k) / (k + 1); what this statement doing?
It is basically $$$\textrm{ceil}$$$$$$(\frac{len}{k+1})$$$, $$$\textrm{ceil}$$$$$$()$$$ being the ceiling function. As C++ $$$\textrm{ceil}()$$$ function can be inaccurate, an alternative to avoid that is $$$\textrm{ceil}(\frac{a}{b}) = \frac{a+b-1}{b}$$$.
Can u pls tell what is wrong in my code- its giving WA on 201 test case https://mirror.codeforces.com/contest/1367/submission/84069351
I couldn't understand the logic, but here's a test case where your code fails:
Expected answer: 1, Your output: 0.
moreover how your coming up with this formula ceil(len/k+1)?
After you obtain a block containing purely zeroes, and there is no restriction on the first table's selection, how do you fill tables optimally? Definitely you can start from the leftmost table, and fill subsequent tables accordingly. For a block of length $$$len$$$ $$$[0,len-1]$$$, you can fill tables $$$0, k+1, 2*(k+1),...$$$ until $$$s*(k+1) < len$$$.
In short, we have to find number of multiples of $$$(k+1)$$$ present in $$$[0, len-1]$$$ (including 0), which is $$$\lceil\frac{len}{k+1}\rceil$$$.
this time editorials solutions are very bad there are other very elegant solutions with less time complexity
yeah I am still not able to understand the approach of problem C and at same time finding my approach slighly easy to understand.
Here’s another solution for E. Upper bound on complexity is $$$O(\sigma(k) \log n),$$$ where $$$\sigma(k)$$$ is the number of divisors of $$$k,$$$ and $$$\sigma(k) = O(\sqrt{k}).$$$
A string $$$v$$$ is $$$k$$$-beautiful $$$\iff$$$ there exists a string $$$\pi$$$ such that $$$v = \pi^m$$$ and $$$|\pi|$$$ divides $$$k$$$.
Imagine we had a magic function, $$$F(p),$$$ that told us the maximum $$$m$$$ such that we can afford $$$v = \pi^m,$$$ for some $$$\pi$$$ with fixed $$$|\pi| = p$$$.
Then we could just iterate over the divisors of $$$k$$$ in order to find divisor $$$p$$$ such that the product $$$p \cdot F(p)$$$ is maximal; that product would be our answer.
Now let’s implement $$$F(p).$$$
We have an upper bound on the number of repetitions of $$$\pi$$$, it is $$$\lfloor n / p \rfloor$$$.
Also, if we can afford some string $$$v,$$$ then we can afford any prefix of $$$v$$$.
So we can do binary search on $$$m$$$ from $$$0$$$ to $$$\lfloor n / p \rfloor$$$ inclusively.
Given $$$p$$$ and $$$m,$$$ how do we check that we can afford $$$v = \pi^m,$$$ for some $$$\pi$$$ with fixed $$$|\pi| = p$$$?
Turns out this is pretty easy: the answer is $$$p \le \sum_{i=1}^{26} \lfloor t_i / m \rfloor,$$$ where $$$t_i$$$ is the number of letters with code $$$i$$$ in the original string $$$s$$$ (e.g., $$$t_1$$$ is the number of letters ‘a’).
It is assumed that $$$\lfloor t_i / 0 \rfloor = \infty, \, \infty + \infty = \infty,$$$ and $$$p \le \infty.$$$ In practice, you should treat $$$m=0$$$ as a special case. Here’s another explanation for it: we can always afford an empty string, even though the final answer (but not $$$F(p)$$$) is always $$$\ge 1.$$$
Code: https://mirror.codeforces.com/contest/1367/submission/84037953
what happened to problem D?
is problem D gone?
Why was problem D removed?
Is problem f actually the famous LIS problem?
Not exactly. It is not just increasing.
Ths subsequence should be a continuous subarray of the sorted array.
i am unable to do implementation if F2 can you help me ...
Then it can be done with a simple two pointer I guess(or am I wrong?) Then why is dp used?
Can you elaborate more on how you use two pointers?
first we iterate over the hole array. let R be 0 at first.(the array is 0_indexed) then let us be on step L of iteration. now as long as you can increase R such that sub array [L, R] is increasing. modify ans by size R — L + 1. (ans = max(ans, R — L + 1)) then at last ans is the answer. tell me if I'm wrong.
Sorry for being unclear.
What I mean is that you should find the longest subsequence(not continuous) of $$$a$$$ such that it is a continuous subarray of $$$b$$$.
I am talking about F1 for simplicity . the case for F2 is little more complicated.
Why the F is problem D removed. It is so unfair. Finally after so long I had a good contest and now I'm so annoyed. The problem didn't seem wrong and if it was there should be some points given to the persons who attempted D first and wasted their time.
@MikeMirzayanov Why is the 4th problem removed? We didn't waste time on it for anything. You should get it back. It didn't seem wrong either
Same bro, wasted so much time on D, would've surely cracked F1 if D wasn't there in the first place.
https://mirror.codeforces.com/blog/entry/78866?#comment-643650 please bother to read this and then say anything
i dont think they remove the problem D deliberately, it's just somethings wrong with the testing system, right?
pls dont remove D, i spent an hour just to solve it
I also spent hours to solve d pls don't remove it
Here is an intuitive and easily implementable solution for E : Consider a nested loop, the inner loop ('j') representing the length of the smallest segment which is repeated over the cycle and outer loop ('i') represents the number of times this segment will occur in the cycle. Both the loops will run from 1 to n. Now we just have to check which pair (i,j) is valid. This can be done easily using an array storing the frequency of each letter in the string and calculating the maximum length of the segment that can be achieved for given 'i'. Refer to the code snippet given below :
please explain line int shift=k%(i*j); if(shift%j!=0) continue in more detail. Thanks in advance
i*j is the total number of beads in the necklace. So shift represents the number of times I need to rotate before achieving the same configuration. I need to ensure that shift is divisible by j because j is the period after which same segment repeat. sum represents the length mentioned in the last line of my previous comment. I hope it's clear now. Ask again if it's still not clear, I will try to elaborate more. Do leave an upvote
Wouldnt it be easier to do F with 2d dp? then its actually pretty simple once you notice the trick to rewrite the array.
People like me who spent a lot of time to solve D are affected. So I think contest should be unrated.
there is an issue in problem D checker and they are fixing it, hopefully it will return soon Your text to link here...
There is a solution for C which is pretty easy. Let's compute prefix sum array for our string. Now let's iterate over string with a window from i-k to i+k and check if there is any '1' already sitting there or not (prefix[min(n,i+k)]-prefix[max(1,i-k-1)]. If it does not then place '1' over there ( increase answer by 1) and go i+k+1 else just do i++.
yaa same i have also done
can somebody help me in implementation of F2
Video Solution to E: Necklace Assembly
can someone help with a bit more clear explaination of probelm F2?? I'm not happy with the above explaination
What is upsolve?
Upsolve means solving problems after the contest.
Why not for F1 editorial? Anyone please explain the logic of problem F1?
F1 is only an easy version of F2. In F1 the constrain are small and some additional conditions are given.
is there anyone explain me problem E editorials briefly? i can't understand the the given editorial.. thanks a lot
check my method in a previous comment https://mirror.codeforces.com/blog/entry/78864?#comment-643686
For $$$E$$$, one could also do the following . Notice that, we must construct strings which are cyclic and repeat after "$$$k$$$ $$$rotations$$$" . Let's think that we need to construct some $$$x >= 1$$$ number of blocks of the form {$$$a_1 , a_2, .. , a_t$$$} , {$$$a_1 , a_2, .. , a_t$$$} , {$$$a_1 , a_2, .. , a_t$$$}, .... $$$x$$$ $$$times$$$. The length of the answer in this case is $$$t * x$$$. We immediately observe that $$$t$$$ must be a factor of $$$k$$$. So, let's loop over all factors of $$$k$$$. For each factor ($$$t$$$) we need to determine the maximum $$$x$$$ that works. Notice, that if $$$x$$$ works, then $$$x - 1$$$ also works. So, we can binary search here . The complexity is $$$O(\sqrt{n} * 26 * log(n))$$$ . Implementation of the above approach : https://pastebin.com/pjajDF0a
I saw someone solved F2 using std::set, here's the link 84018692. Can someone help explain it? Or can anyone tell how to solve F2 with shorter length of code?
Wow, this solution is very clean, no DP needed at all. The basic idea is as follows: we can pre-sort all of our values and use two pointers to find the largest segment that appears as a subsequence in the original array. Now, say your sorted elements are [0, 0, 1, 1, 2, 2]. If we wanted to find out whether, say, [0, 1, 1, 2] appears as a subsequence in our original array, we need the following observation: we need all of the middle elements (i.e. 1's) and only some 0's and some 2's. Which 0's and 2's should we take? Well, it would make sense that we should take the earliest 0's that appear and the latest 2's that appear. This is the core idea behind that solution.
Now, to explain the actual code: v stores {element, -index} pairs and sorts it so that when we start iterating over a new element, we will be looking at the latest occurrence. The set s1 stores the indices of all of the elements of the current value, and the set s stores the indices of all the other elements that are currently in our subsequence (note that the segment from [i, f] is the current subsegment). To decide whether we can add a new element, we essentially need to make sure that the only elements in s are the ones that appear after our current one, so we increment our back pointer and delete from the set until this is the case.
At the end of each iteration, s and s1 contain the indices of the longest subsegment of the sorted array ending at index f that can be found as a subsequence in the original array, so we update our answer with the current subsegment size.
It's a really strange idea. With the help of your extremely clear explanation, I now understand how it works. Atfer sorting, the author's aim is to find a longest subsegment which satisfies some kind of restriction as the following picture shows.
Then when adding a new element, we need to delete those elements illegal in s as the following picture shows.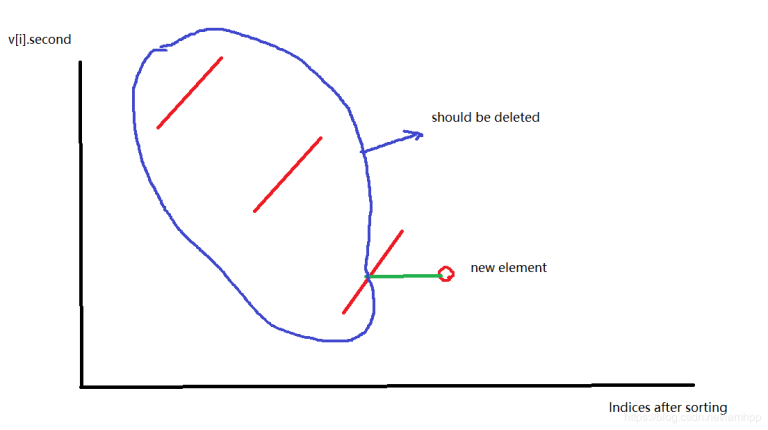
And actually, s1 is not needed. It can be replaced just by a stack.
Thx a lot for your clear explanation!
Thank you so much iamhpp and Kognition for this solution! This is a very elegant and concise way to solve such a difficult problem.
Here's a similar question to Problem F (Flying Sort): Click.
I remembered I did this before and I was looking for this problem during the contest but couldn't find it. Thanks for bring this out!
I'm not understand dynamic programming approach in F2. Can someone give me example and simulate step by step ? What's dp[1], dp[2] , .....so on in this example ? What's the relation between dp[i] and dp[i-1] ? Thanks.
I am not able to understand the following lines that were written in the editorial of the f2 question ( refer last line of the editorial contest 650 of problem f2). can anyone explain me? It is necessary to separately consider the first numbers in the subsequence and the last, since the first should include their suffix, and the last should have their prefix.
In the last sample problem, of F2 After modifying the array,
20
16 15 1 10 0 14 0 10 3 9 2 5 4 5 17 9 10 20 0 9
It becomes,
20
10 9 1 7 0 8 0 7 3 6 2 5 4 5 11 6 7 12 0 6
and the highlighted ones are sorted largest sorted subsequence in length 5 so the answer should be 15, or am i missing something.
Can anyone please explain how the answer is 10 in the fifth sample case of E
20 5 ecbedececacbcbccbdec
answer->10
For D in the editorial code, how are we ensuring that we aren't picking a letter which appears lesser times in S than needed?
Can Someone Explain this following line in the editorial of Problem C.
"then in each block we can put [number of zeros/k]".
Suppose Example is n=6 k=1 So maximum tables will be 3 but according to this formula answer will be 6 i.e (6/1)
Any Catch which i am missing?
No, the editorial is wrong.
Thanks spookywooky for replying,
I checked the solution there it's written (len+k)/(k+1). Can you explain me how our we getting this formula?
The blocks (ie. len) is of calculated length, see the three points above in the editorial. Then, the meaning of len is as if the whole string would be of len zeros. No 1 left, no 1 right.
In such a string we can put a 1 at first position, then for every block of k+1 positions one more. This is exaktly (len+k)/(k+1)
I would have preferred to write (len-1)/(k+1) + 1, which is the same.
why (len+k)/(k+1) ? and not (len)/(k+1)? Not able to get it.Can you explain?
You can put a 1 at position zero. Then you are left with len-1 items, and can place (len-1)/(k+1) items. So answer is (len-1)/(k+1)+1
Since $$$(a+b-1)/b = (a-1/b)+1$$$ it is that $$$(len-1+k+1)/(k-1)=(len+k)/(k-1)$$$
I am very much near to it brother Just one thing i wanna ask,
Why it is (len+k)/(k+1) and not (len+k)/(k)?
If the string is like 1000000... and has n zeros, then you can place n/(k+1) ones in it.
Because you need to let k zeros as is, then change one to '1', and so on.
Can anyone help me understand these last lines of F2 editorial — It is necessary to separately consider the first numbers in the subsequence and the last, since the first should include their suffix, and the last should have their prefix.
I didn't understand too, until I figured it out my self. For that test case:
20
16 15 1 10 0 14 0 10 3 9 2 5 4 5 17 9 10 20 0 9
After indexing it it will be:
10 9 1 7 0 8 0 7 3 6 2 5 4 5 11 6 7 12 0 6
I thought that the answer is taking 3,4,5,6,7 and the answer will be 15 but this is wrong! Because There is another 5 between 3 and 4 that you can't throw it at the beginning or at the end. So the first number and the last number in the subsequence you can take parts of the occurnces of them. But the numbers between the first and the last all the occurences must be taken in the subsequence. Hence the answer is take 5 5 6 6.
I can't understand the editorial for problem F2. Can anyone explain me what's wrong?
That is, the task came down to finding the maximum sorted subsequence in the array. So if we have testcase:
The max sorted subsequence in the array will be
0 1 2and the answer will be (n = 5) — 3(length of the max sorted sequence)? But if we move 4 to the right we can get sorted sequence only in one move?In the original array, you just need a non-decreasing subsequence(not necessarily contiguous), but those values must be contiguous in the sorted array (otherwise you would have to insert something in between them without moving the elements themselves, which is impossible with given operations). So the max sorted subsequence is 0 1 2 3 because it is contiguous in the sorted array but is a non-decreasing subsequence in the original. Therefore the answer is 5 — 4 = 1 as expected.
Thanks! Got it.
In F , for the case: n=4 , a=[0,2,1,3] longest sorted subsequence is 3 , then as per editorial answer is 1 (4-3=1) right ? But expected answer is 2 ? Can someone explain what i am understanding Wrong ?
It is supposed to be the longest non-decreasing subsequence that is contiguous in the sorted array. In this case, the sorted array is [0, 1, 2, 3]. The only longest subsequences that satisfy this are [0,1] and [2,3]. There is no contiguous set of 3 elements in the sorted array that are non-decreasing in the original. So as per the editorial, 4 — 2 = 2.
Missed the point that elements have to be continuous .got it now . Thanks
Can someone explain the implementation of F2. When doing the dp for the longest non-decreasing subsequence, how is the 'contiguous in the sorted array' requirement checked? Also isn't LIS an O(n^2) dp, so how does it fit in time constraints?
why (len + k)/(k + 1) in problem c. why not (Len)/(k) ??
Check the comments before
If anyone is stuck in C here is some example with case discussed in the tutorial Here
In anyone of you is wondering why your code for F2 failed for test case : 3(4999th), well it's because you didn't consider that case when your subsequence will contain two different elements.
For the sake of reference here is the test case:
t = 1n = 20array = 3 2 7 9 14 8 6 11 10 7 5 7 2 8 8 4 7 1 13 12 16answer : 15,if yours is 16 this might be the reason
My submission AC: i too ignored that case :)
Can anyone please explain what is dp2 and dp3 for in problem F?
I'll try to explain my solution of 1367F2 - Flying Sort (Hard Version) in details.
Disclaimer: it's hard way to solve it.
I'll describe things in order how I was solving it.
First, I checked: is any element moved only once? The answer is yes. Proof is following.
Suppose that there is some element you had to move multiple times. Throw off all moves of this element except last move. Sequence in the end is same, so we got better answer. Proved.
Second, I checked: how to sort array using only moves to the left? Well, main observation: all moved elements form a prefix of array. This means, if any element should be moved, then its final position should be within the prefix. But we know the prefix should be also sorted, so all elements less than the value of moved element should be also moved. We need to minimize number of actions. It's same as minimize length of prefix. Assume that there is no elements with same value. Then, by definition of "highest" moved element we know that all other elements won't move, so finding highest moved element is equivalent to find first stationary element, and equivalent to maximizing length of suffix with elements not moved. Then algorithm is: find minimum element that should not be moved, then move all elements with value less than it in decreasing order. How to find lowest element that should not be moved? Well, iterate array values in decreasing order while their positions are decreasing. All those elements don't need to be moved. So last elements in this list is highest stationary element, and first element with position higher than previous should be moved. Algorithm to sort using only moves to the right is similar.
Regarding to assumption about no similar elements: I was solving simple case first, so I'll mention it later.
Third. Is there always stationary element? Yes! Proof: assume for some input optimal answer is to move all elements. Pick any element as stationary. Move all elements with value less than stationary to the right in increasing order. Move all elements less than stationary element to the left in decreasing order. We got sorted sequence. So, this answer is better. Contradiction.
Fourth. We know that elements split into three parts: stationary, moved to the left, moved to the right. Also, there is always at least one stationary element. From nature of operations follows, that moved to the left elements form a prefix, and moved to the right elements form a suffix, and stationary elements all in between.
Summary:
My idea is following. We don't know which element is stationary. Try each element as if it is stationary. But there is two issues to deal with: we don't know how many other stationary elements, and elements that should be moved to right is interleaved with elements that should be moved to the left.
Let's deal with "interleaving" first. (Still taking assumption that there is no similar elements) From fact that element is stationary, means that all elements with higher value, should be in front of it. Similarly, all elements with less value should be after it. This means, that if any element with value higher than stationary element and in front of stationary element, it will be moved to the right. So, we only need to consider elements with value below stationary element for using "move to the left", and sort only them with it. All other values will be moved to the right and don't interfere. Similar thing holds for "move to the right".
Now, let's deal with number of stationary. My solution to this issue is: there is always rightmost stationary element. Thus, try each element as if it is rightmost stationary element.
So, for tests without duplicates of numbers, my solution is following: try each number x as rightmost stationary. build list of numbers less than x and greater than x, use algorithm above to sort both sequences, and take minimum of steps among all options among x. You can find all.
To solve general case, we need to revisit algorithm to sort sequence using "move to the left" action, and "interleaving". In algorithm we use difinition of "highest" not moved. Now, last moved element can have same value as first stationary element. Moved with the same value as stationary can be only after value next in sorted list.
To make clear, I'll state task for sorting using move to the left only. We consider only those numbers with values not exceeding picked as stationary. Also we have position of picked number. And we wan't to not move it, and sort every value below it into increasing subsequence. I'll use brackets for picked number. Examples:
Third example is to show how values above stationary are ignored. Last two cases are general cases. Crucial undestanding is in them. So there are two cases:
Second case case is most tricky. If rightmost position of previous group by value doesnt exceed, then we need to recursively solve for rightmost of previous group. Otherwise, we have to move rightmost of previous group, thus we can calculate how many elements we need to move.
Alright. This was coded by me in few hours, with some mistakes though, but nevermind. Most complicated thing is ahead. Now we need to consider both directions. Now we can move in both directions. And here is the most trickiest case, and it's luckly straight in the samples:
Looks like trivial. But! Where is here rightmost stationary? It's last element! But it shows general idea. You can partialy shift group to the right. Probably you can handle that using two dp in both directions, but I didn't want to do that, so I just tried to move each prefix of group to the right. As long as I know that picked element is rightmost stationary, I don't need to sort anything to the right, I only sort to the left, and every other element which is greater value considered as moved. And some prefix of current group is considered to moved to the right. It took a day to debug all stuff.
Summary:
Here is version of code with debug. 84434347 It has reconstruction of sequence of actions, and checker. And here is cleaned code. 84513543
Problem E: I'm not sure I understand why it is okay to solve the "last part " with a simple greedy algorithm.
If I have cycles of length 4, 4, 5 and I have letters with counts 5, 8 then the greedy algorithm will say it is not possible to make a selection but in fact 8=4+4 and 5=5 so it is possible. Is there something I'm missing>?
Yes, I also had the same doubt, thanks for the counter case man. I tried to prove the greedy algo, but wasn't able to.
UPD: solved it.
Can somebody please tell me what's wrong with my solution for problem B? 128827323
In the editorial for 1367E — Necklace Assembly, can someone explain how the last part's greedy solution is correct? i.e. distributing the beads in each cycle, why taking the maximum at every step works?