315A - Сережа и бутылки
Просто для каждой бутылки проверим, можно ли открыть ее другой. В данной задаче проходили абсолютно любые решения.
315B - Сережа и массив
Будем поддерживать все элементы в массиве, но дополнительно заведем переменную add: сколько нужно добавить ко всем элементам. Тогда про добавлении ко всем элементам просто увеличим add. При выводе будем выводить элемент массива + величину add. При обновлении будем ставить элемент равным значению, которое нужно поставить минус текущая величина add.
314A - Сережа и контест
Заметим, что если мы удалили некоторого участника, то мы никогда не удалим участников с меньшими номерами, так как их сумма будет только увеличиваться. Поэтому просто последовательно рассмотрим всех участников, и если участник не подходит, то удалим его.
314B - Сережа и периоды
Понятно, что можно жадно искать количество вхождений 2й строки в первой, но такое решение работает долго. Для ускорения процесса можно искать в первой строке строку, которая задает период второй. А ответ поделить на то, сколько строк нужно для задания второй строки. Далее рассмотрим наш жадный алгоритм. Мы идем по первой строке, пока не встретим первый символ второй строки, потом второй, третий и так далее до последнего, потом снова ищем первый, второй и так по циклу. Понятно, что когда мы дважды окажемся в состоянии, в котором позиции в первой строке соответствует одному символу строки, которая задает период и позиции во второй строке одинаковы, то мы получим период. Когда мы найдем этот период, то просто повторим его столько раз, сколько возможно, что бы каждый раз не считать одну и ту же информацию.
Для лучшего понимая, советую прочитать любое прошедшее решение.
314C - Сережа и подпоследовательности
Понятно, что нужно посчитать сумму произведений элементов всех различных неубывающих подпоследовательностей заданной последовательности. Будем идти по последовательности слева направо и поддерживать массив q[i]: какая сумма всех нужных подпоследовательностей, таких что их последний элемент равен i. Понятно, что если очередное число это x, то нужно поставить q[x] = sum(q[1]+q[2]+...+q[x])*x+x. Ответом на задачу будет сумма всех q[i]. Для нахождения всех сумм можно использовать дерево Фенвика.
314D - Сережа и прямые
Повернем все на 45 градусов с помощью преобразования: (x, y) -> (x', y'): x' = x+y, y' = x-y.
Далее нужно разместить две прямые параллельно осям координат. Отсортируем точки по первой координате. Далее будем использовать бинарный поиск по ответу. Пускай мы зафиксировали некоторое число, теперь нужно проверить хватит ли его, или нет. Заметим, что сейчас нужно разместить две полосы ширины 2 * зафиксированная величина, что бы ими покрыть все точки. Допустим, что некоторая точка будет прилегать к левой стороне вертикальной полосы, далее для всех точек, которые не попадают в полосу найдем минимальную и максимальную вторую координату. Если разница между найденными координатами не больше 2 * зафиксированная величина, то полосы разместить можно, иначе — нет.
Скоро...
Украина выиграла матч! Теперь можно и разбор писать)
Фух, теперь болеем за Россию :)
Нет такого слова "ихняя".
Всегда Ваш Grammar Nazi
Сколько вариантов-то перепробовал)
Excellent problem set. Kudos, Sereja
Слово "понимаю" есть, но здесь как-то не смотрится...
(в конце разбора 314B)
Автор, когда исправляешь показанные тебе опечатки, стоит как-то комментировать, например, благодарить указывающего. А то минусуют...
Может быть, для этого есть личные сообщения?
Может быть, но с другой стороны, здесь этот комментарий увидят и учтут многие, а в ЛС — только почтеннейший Sereja.
Но безмозглость некоторых представителей местной публики поражает, конечно. Как будто это сайт поклонников телепередачи "дом-2".
Да, спасибо что поправил.
Но лучше пиши в лс, так как когда я отвечаю, то тоже получаю минусы(почему же?).
Нееет, ты-то как раз наварился...
Awesome problemset, In (314A — Sereja and Contest): How to avoid overflow of long long? (i-nDelete) * (n-i-1) * d[i]. This number can be really large, about 1e19. Thank you.
You dont need to calculate this number. What you really need, is to calculate (i-nDelete) * (n-i) * a[i]. Just look at any solution.
(i-nDelete) * (n-i) * a[i] seems to be 1e19 in worst case... Moreover, if rating was from 0, 1e19 would really appear in test like "0, 0, ..., 0, 1000000000, 0, ... 0" with 1000000000 in the middle of sequence. But rating is >= 1, and it doesn't work in test "1, 1, ..., 1, 1000000000, 1, 1, ... 1"...
Could you (or anybody else) proof (or give a countertest) that honest solution with long long really works?
(i-nDelete) * (n-i) = i * n — i * i + i * nDelete — n * nDelete = i * (n — i + nDelete) — n * nDelete
If we want to reach the maximum, its better to minimize "n * nDelete", and maximize "i * (n — i + nDelete)". But, as we know, i <= n, so its better if nDelete == 0. (Because if we increase nDelete by one, we will increase all sum by i — n <= 0).
It can be seen, that the maximum would be reached if (i = n/2) and (n * nDelete = 0). It meens that
max = i * (n — i) — n * nDelete = (10^5)/2 * (10^5)/2 — 0 = (10^10)/4
a[i] <= 10^9
max * a[i] <= (10^19)/4 < MaxLL
The problem is that maxn in this problem is 2*10^5, so in your argumentation we see max = (10^5) * (10^5) = 10^10 without any 2 or 4...
n <= 2 * 10^5, and in your proof max = 10^5 * 10^5 — 0 = 10^10. Then max * a[i] <= 10^19 > MaxLL.
Oh, yes...I thought that n doesnt exceed 10^5. Im sorry.
It is very easy. You can calculate this number in double, becouse |K| is near 10^9.
If we want to company a double number(indicated by D) with K, we can easily compare D and K with a little eps like 1e-10, right? If K is about 10^18, we can not do that directly. Anyway, Nice method to overcome the overflow of long long.
In 314C — Sereja and Subsequences
There exists condition that some elements are same and the solution will probably make mistakes on it.Maybe we should use an extra array to deal with it.
example:
3
2 2 2
The right answer is 14,but it will print 26 with the solution See my codes for details
I used the editorials idea and my solution prints 14 for your input. Maybe you thought three different indices will be updated for the input, yielding the array
q[]with values 2, 6, 18 and final answer (of course wrong) 26. But in fact onlyq[2]will be updated thrice for the given input, 2, 6, 14 being its values and 14 being the last answer. Is it clear?I have checked some AC solutions for problem E. It seems that they all used an O(n^2) dp to walk through.
Is the model solution also this kind? I guess that it is not that suitable to put an O(n^2) solution with n = 10^5, though it runs faster than it might be expected.
For my solution worst testcase is all '?'. So i just wrote it. Got 7 seconds local, TL on run. Some hacks -> 1.8 seconds local,2 on server. I think it's fair enough. Everybody can wrote this and check.
If author solution is better, i can't understand why there was modulo 232. There was no chance using other modulo.
Could anyone explain DP approach in problem E?
Let's assume that we have a brackets sequence(lowercase letter is an opening bracket, uppercase letter is a closing bracket).
Let dp[i][j] = number of ways to reconstruct the string such way that first i characters are already processed and there're j opening brackets which are still not closed.
Then dp[i][j] = dp[i — 1][j — 1] if s[i] is a lowercase letter, (it can just be a one more opening bracket)
dp[i][j] = 25 * dp[i - 1][j - 1] + dp[i - 1][j + 1] otherwise. ('?' can be both: an opening and a closing bracket).Now it's clear how to calculate this dp in O(n^2) time. With some constant optimizations this solution gets AC.
Кто-нибудь, обьясните пожалуйста решение задачи D как можно подробнее.
Я не совсем понимаю, что непонятно в разборе. Для лучшего понимания лучше прочитать любое прошедшее решение, там просто очевидно все: что и как.
Прочитал еще раз, почти все понятно. Остался один нубский вопрос. Почему преобразование такое?
Это стандартный поворот точек на 45 градусов. По идеи через матрицу поворота выводится.
В каком смысле выводится — это и есть матрица поворота. На самом деле это не просто поворот — еще растяжение в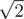
раз. Видимо еще в композиции с какой-то симметрией даже.
Поворот на угол φ задается формулами
Возможно я перепутал знак - и получился поврот на - $\varphi$ Видно что с точностью до какого-то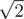
и знака при повороте на 
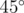получится ровно то, что надо.
А почему в растянутых координатах ответ не увеличивается?
Они растянуты с точки зрения Евклидовой метрики. И если бы мы брали расстояние по перпендикуляру, то изменился бы.
Та метрика которая у нас была перешла как раз в максимум из модулей разности координат. Проверяется явным вычислением.
Почему именно такое преобразование поворачивает на 45 градусов? А Вы вспомните школьный курс тригонометрии: если есть вектор с координатами cos(x), sin(x) и его поворачивают на угол y, у полученного вектора будут координаты cos(x)*cos(y)-sin(x)*sin(y), cos(x)*sin(y)+sin(x)*cos(y). В данном случае sin(y)==cos(y)=sqrt(2)/2. Так что, получается вектор sqrt(2)/2* (cos(x)-sin(y), cos(x)+sin(x)). Ну и остаётся заметить, что порядок координат и мультипликативная константа неважны.
Can you post the submission ID of your accepted solution for 314B — Sereja and Periods. Thanks in advance.
Roll all at 45 degrees using the transformation: (x, y) -> (x ', y'): x '= x + y, y' = x-y. can someone explain that to me please? i thought rotatating 45 degrees was something like multiply by (sina+cosa)
For 314B, we don't need to find the "circle". I've read several AC codes and can hardly figure out their ways to find the circle. Finally I got the core that we can easily calculate how many letters of the String C can we get in [a,b].
Firstly we can nest two loops to find out: if we start with the ith character of String C and the first caracter of String A, how many following caracters of String C can match the caracters of String A one by one. It goes like this: for (int i=0; c[i]; i++) for (int j=0; a[j]; j++) if (a[j]==c[(i+f[i])%m]) f[i]++; //m is the length of String C
Secondly we simulate the process of [a,b]. Obviously, we start with the first caracter of String C. Then we add f[0] to ans. The second time we start with the (f[0]%m+1)th caracter of String C and we add f[(f[0]%m+1)%m] to ans that is f[ans%m]. Each time we plus a String A, we can easily know how many caracters can we match in String C by using array f. It goes like this: for (int i=0; i<b; i++) ans+=f[ans%m];
Finally we divide the ans by m and d and get what we want.
Thanks for your explanation, It has confused me for a long time. Your explanation is quite understandable!
Блог старый, но всё же может кто-нибудь поймёт меня и ответит — почему в 314C — Сережа и подпоследовательности в формуле пересчёта в конце идёт +x ? (q[x] = ... + x)
Потому что число x либо продолжает уже существующую подпоследовательность (которая заканчивается на 1 или 2 или 3 ...или х и даёт вклад (q1 + q2 + ... + qx) * x), либо создаёт новую подпоследовательность длины 1 (и даёт вклад x).
Прошло 3 года, а разбора задачи Еdiv1 до сих пор нет. Кто знает как ее решать напишите пожалуйста в комментариях разбор.
The testcase 33 for the problem 315A Sereja and Bottles:
has the answer given by system as 1, whereas the correct answer has to be 0. (Opening the bottles of brand 2,3,4 is trivial, but first bottle of brand 1 can open second bottle of brand 1, which in turn can open the first bottle of brand 1, as any (open or closed, doesn't matter, as stated in problem.) bottle of brand 1 opens any other bottle of brand 1).
I understand this is necroposting, but I am writing this for the future people who come here from Codeforces ladder (How I came to this problem) so they can understand the problem with the problem's answer. If anyone finds a mistake in the argument above, I will be grateful to get a constructive feedback.