Предварительная версия разбора.
В задаче про четные и нечетные числа требуется понять, как будет выглядеть последовательность чисел от 1 до n, если выписать сначала все нечетные числа, а затем — четные. Для того, чтобы определить, какое число стоит на k-м месте, нужно посчитать индекс в массиве, с которого начнутся четные числа, и вывести соответствующее k либо нечетное число из первой половины массива, либо четное из второй.
В задаче про хэви-метал требуется найти в строке S количество подстрок, начинающихся на одну строчку A и заканчивающихся другой строчкой B. Если мы пометим черным все позиции вхождения в S строки A, белым — позиции вхождения строки B, то получим следующую задачу: посчитать количество пар <черная позиция, белая позиция> (причем именно в таком порядке). Для этого достаточно бежать, к примеру, слева направо и хранить счетчик — количество уже пройденных черных позиций. Тогда если мы встречаем очередную черную позицию, то увеличиваем счетчик на один, если встречаем белую — добавляем к ответу количество пар с данной белой позицией. А это количество — и есть текущее значение счетчика.
Как легко понять эта задача была задачей на аккуратность. В ней труднее не придумать решение, а написать его так, чтобы ни один случай не был забыт.
Каждый ход мы заменяем одно из чисел x, y на их сумму x + y и так пока пара чисел на доске не станет m-превосходной (то есть одно из чисел станет не меньше m). Ясно, что заменять на сумму нужно именно меньшее из двух чисел x и y. Действительно, будем говорить что пара чисел x1 ≤ y1 мажорирует пару чисел x2 ≤ y2, если y1 ≥ y2 и x1 ≥ y2. В этой ситуации, если за несколько наших действий из пары x2, y2 мы получим m-превосходную, то применяя те же самые действия к x1, y1 мы получим m-превосходную пару никак не позже. Если x ≤ y, то пара x + y, y мажорирует пару x + y, x. Поэтому путь через x + y, y до m-превосходной никак не длинее, и можно считать что мы выбираем именно эту пару. Теперь действия нашего игрока однозначны.
Рассмотрим случаи:
x ≤ 0, y ≤ 0 В этом случае наши операции не увеличивают числа на доске, поэтому пара может стать m-превосходной только если она изначально была m-превосходной.
x > 0 или y > 0 В этом случае для любого m пара со временем станет m-превосходной. Для того чтобы посчитать точное количество шагов теперь достаточно запустить эмуляцию. Однако если при x > 0 и y > 0 легко видеть что пара <<растет экспоненциально>> (формальнее: лекго видеть что начиная со второго шага сумма x + y увеличивается хотя бы в 3 / 2 раза за каждый ход) и эмуляция работает очень быстро, то в случае x < 0 и y > 0 (или наоборот) числа в паре могут изменяться очень медленно. Особенно хорошо это видно на примере x = - 1018, y = 1. Поэтому в таком случае необходимо отдельно посчитать количество шагов до момента, когда оба числа станут неотрицательными и только потом запускать эмуляцию. Для x < 0 и y > 0 такое количество шагов равно
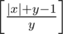 .
.
Задачу можно представлять себе следующим образом. В вершинах двумерной решетки 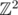 расставлены неотрицательные целые числа A(x, y). Считаем, что они заданы функцией
расставлены неотрицательные целые числа A(x, y). Считаем, что они заданы функцией 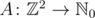 . В каждый момент времени для каждой вершины P = (x, y) с числом A(x, y) ≥ 4 применяется операция φP, которая уменьшает A(x, y) на 4 и увеличивает A(x, y - 1), A(x, y + 1), A(x - 1, y), A(x + 1, y) на 1. Можно считать, что операция φP применяется ко всей функции A. От нас требуется найти эту функцию в запрашиваемых узлах после того как итерации прекратятся.
. В каждый момент времени для каждой вершины P = (x, y) с числом A(x, y) ≥ 4 применяется операция φP, которая уменьшает A(x, y) на 4 и увеличивает A(x, y - 1), A(x, y + 1), A(x - 1, y), A(x + 1, y) на 1. Можно считать, что операция φP применяется ко всей функции A. От нас требуется найти эту функцию в запрашиваемых узлах после того как итерации прекратятся.
Ключевое наблюдение для большинства решений состояло в том, что операции φP и φQ для всех точек P и Q коммутируют, то есть φP(φQ(A)) = φQ(φP(A)). Поэтому неважно в каком именно порядке применять операции. В частности, можно считать, что из данной вершины разбегаются сразу все возможные четверки муравьев. Теперь можно запустить прямую эмуляцию процесса в таком виде. В качестве упражнения участникам предлагается проверить, что муравьи никогда не покинут квадрат 200 × 200 с центром в 0 при указанных ограничениях.
В задаче про сосуды и воду требовалось найти последовательность из порядка n2 переливаний, которая переводит начальную конфигурацию в конечную. Во-первых, утверждается следующее: если в каждой компоненте связности сумма исходных значений и сумма итоговых совпадают, то ответ существует. Назовем сосуд готовым, если текущее и требуемое количество воды в нем совпадают. Опишем сначала решение, которое, вероятно, проще всего пишется. Будем делать сосуды готовыми по очереди. Возьмем произвольную пару еще не готовых сосудов s и t (в s сейчас воды больше, чем нужно, в t — меньше, чем нужно), такую, что их соединяет некоторый простой путь P, при этом если перелить из s в t d литров, то один из сосудов станет готовым. Осталось научиться переливать d литров по пути из s в t. Напишем для этого рекурсивную функцию pour(s, t, d). Пусть t' идет перед t в этом пути, тогда функцию выполнит следующее: перельет из t' сколько возможно (разумеется, не больше d) в t, вызовет pour(s, t', d) и затем перельет из t' в t то, что осталось. Несложно проверить, что никакой сосуд при этом не переполнится. Такой алгоритм производит переливание по пути длины len за 2len элементарных переливаний, в итоге решение делает не более 2n2 операций.
Давайте для каждого числа x обозначим последовательность его степеней не вылезающих за границы [1..n] через Pow(x): 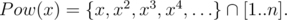
Тогда наша игра состоит в следующем: каждый игрок на очередном шаге выбирает еще не зачеркнутое число x от 1 до n и зачеркивает все числа из Pow(x). Проигрывает не имеющий хода.
Легко заметить, что такая игра распадается в сумму нескольких более простых игр. Действительно, назовем число x примитивным (и соответствующую последовательность Pow(x) примитивной), если оно не является степенью никакого числа y < x. Тогда: 1. для любого числа 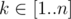 найдется примитивное число x, такое что
найдется примитивное число x, такое что 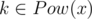 ; 2. для любых различных примитивных чисел x и y множества Pow(x) и P(y) не пересекаются. Действительно для данного числа k существует ровно одно примитивное x степенью которого k является. Это, например, следует из основной теоремы арифметики: если
; 2. для любых различных примитивных чисел x и y множества Pow(x) и P(y) не пересекаются. Действительно для данного числа k существует ровно одно примитивное x степенью которого k является. Это, например, следует из основной теоремы арифметики: если 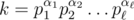 и d = gcd(α1, α2, ..., αn), то
и d = gcd(α1, α2, ..., αn), то 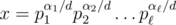 .
.
Таким образом все множество [1..n] разбивается на маленькие примитивные подмножества Pow(x), игра на которых происходит независимо. Наша игра распалась в сумму меньших игр. Теперь необходимо применить теорию Шпрага-Гранди и заметить, что мекс-функция нашей игры является ксором мекс-функций всех игр на примитивных Pow(x). Среди таких игр много совпадающих, что позволит легко вычислить ксор.
Для конкретного x, если Pow(x) = {x, x2, ..., xs}, то мекс-функция зависит только от s, но не от самого x. В наших ограничениях s принимает значения от 1 до 29, мекс-функции для всех таких s можно предподсчитать напрямую. Осталось теперь лишь найти количество q(s) примитивных x с данной длиной Pow(x) равной s (более точно нас интересует не количество, а лишь четность этого количества).
Ограничения задачи позволяют сделать это "в лоб": увеличиваем x от 2 до  , если оно не зачеркнуто, находим длину Pow(x) [увеличиваем соответствующее q(s)], и зачеркиваем все числа из Pow(x).
, если оно не зачеркнуто, находим длину Pow(x) [увеличиваем соответствующее q(s)], и зачеркиваем все числа из Pow(x).
Этот цикл найдет все примитивные последовательности длины хотя бы 2. Количество незачеркнутых чисел даст все примитивные последовательности длины 1. Останется лишь посмотреть на их четности и посчитать соответсвующий ксор мексов.
Однако можно найти все q(s) и за 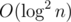 . Действительно, давайте посмотрим какое-нибудь число
. Действительно, давайте посмотрим какое-нибудь число 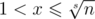 и последовательность {x, x2, x3, x4, ..., xs}. Она не является примитивной, только если содержится как подмножество в некоторой большей примитивной последовательности. Количество таких подпоследовательностей длины s в данной примитивной последовательности длины t > s легко найти, действительно это [t / s]. Вспоминая теперь, что притимвные последовательности не пересекаются получаем реккуретную формулу
и последовательность {x, x2, x3, x4, ..., xs}. Она не является примитивной, только если содержится как подмножество в некоторой большей примитивной последовательности. Количество таких подпоследовательностей длины s в данной примитивной последовательности длины t > s легко найти, действительно это [t / s]. Вспоминая теперь, что притимвные последовательности не пересекаются получаем реккуретную формулу
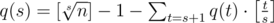 .
.
Используя ее, легко найти все q(s) начиная с q(29) и заканчивая q(1).
Замечание: при написании задачи важно не забыть учесть примитивное x = 1.
В задаче про принцессу Владу требовалось всего-навсего поймать тень. Опишем идею решения. Если на плоскости растет всего одно дерево, то, используя его как преграду для тени, несложно найти подходящую последовательность ходов. Аналогично поступим (использовав какое-либо крайнее дерево), если Влада и Тень находятся далеко, вне квадрата, где могут расти деревья. Осталось понять, что же делать в самой чаще леса! Если между Владой и ее тенью вообще не существует пути, то поймать тень никак не удастся. Иначе рассмотрим кратчайший путь от принцессы до тени, и пойдем принцессой по нему. Будет считать, что этот путь задает нам очередь шагов, которые необходимо сделать. При этом если тень передвигается куда-либо, то добавим ее ход в очередь (иначе говоря, мы идем по пути, состоящему из кратчайшего пути до тени в начальный момент времени и последующих передвижений тени). Алгоритмическая часть на этом закончилась: утверждается, что мы за необходимое число шагов либо поймаем тень, либо выйдем из "лесного квадрата". Доказательство опирается на следующую идею: длина пути, по которому мы идем до тени, разве что уменьшается. При этом если она не уменьшается достаточно долго, то раз в k шагов (k — длина пути) происходит смещение на один и тот же ненулевой вектор, следовательно, мы выйдем из "лесного квадрата". Стоит отметить, что если наши герои не заперты в лабиринт (могут выйти из "лесного квадрата"), то можно вывести их из квадрата по очереди. Но в таком случае для лабиринта все равно придется придумывать способ ловить тень.










Разбор сразу появился. Даже до окончания систестов. Это хорошо =)
В задаче Е такое решение понятно, но есть вопрос: я собираюсь пройти очередь и потом опять же идти по кратчайшему пути. Это фейл или нет? Если да, скажите идею теста.
Upd. немного неясно выразился, я собираюсь повторять следующее: выписать кратчайший путь, пройти его, повторять, пока мы не в одной точке с тенью.
Понятно, что в итоге это приведет нас к тени, по тем же причинам, что и в авторском решении. Единственная трудность с таким подходом это время, которое тратится каждый раз на поиск кратчайших путей. Однако ограничения в условии настолько маленькие, что такое решение должно проходить, особенно если случай "открытого" леса обрабатывать отдельно.
"мекс-функции для всех таких s можно предподсчитать напрямую"
Можно пожалуйста поподробнее как это предполагалось делать? Мне пришлось использовать преподсчёт используя 2^29 масок — какие s из данного набора были вычеркнуты. Как можно найти мексы в рантайме?
Именно такой прямой предподсчет и подразумевался. Набор мексов надо именно найти заранее, в рантайме только проксорить их.
У меня он работал минут 10. Я что-то делаю не так? Почему нельзя было сделать ограничения до 10^8?
несколько секунд у меня с O2 на C++. а вот еще в 2 раза больше — уже бесконечно долго ибо с памятью проблемы. (Вероятно помогло закрытие джавовских идешек)
Предполагалось запустить dfs от полной маски [1..29]. Он попутно найдет все мексы на масках [1..k]. Это должно работать (и у нас работает) довольно быстро, например потому что многие маски не достигаются.
А, тогда понятно, я для всех масок считал...
У меня работал 6 минут. Я особо не заморачивался, считал для всех масок и получил 2^29 * 29^2.
Весело было когда я вместо <= написал <, он не вывел мекс для 29 и пришлось ещё 6 минут ждать...
А зачем 29^2?
Когда знаем маску, перебор по вычёркиваемому числу (29), а потом надо вычеркнуть все его множители (ещё 29), чтобы получить маску откуда смотреть.
А, вот так) Я уже думал, что mex через квадрат считался.
Это же одной маскировкой mask &~ mask_pick[i] делается. И потом, само по себе это логарифм, как решето эратосфена.
Да, мне было в лом делать маски, и я всё конвертил туда-сюда-обратно в булевский массив. Ключевая фраза: "я особо не заморачивался".
Да, про логарифм согласен, ок, спасибо.
Я все-таки думаю, что в онлайне должно работать следующее: пишем dp по достижимым маскам в порядке этого комментария, для индексации за O(1) используем стандартный трюк: прекалькаем для всех 16-битных чисел количество единиц в начале числа (например, для числа 3 это 2, как и для числа 13), ифая старшую/младшую часть умеем это находить для произвольного 32-битного числа и используем двумерный массив [число единиц][номер маски]. Получается порядка достижимых_масок*29*2 операций.
А сколько из них достижимые? У меня получается в духе 2^24 оценка.
Upd.
не более — вид маски (учитывается, что если в позиции 0, во всех кратных тоже 0)
1 — 0*
2^14 — 10*
2^18 — 110*
2^19 — 1110*
2^19 — 11110*
2^19 — 111110*
2^18 — 1111110*
...
3898005 — решение в онлайне. Идея та же, что и при прекалке, но соптимизировано до 750мс. Из них на само вычисление функций Гранди уходит около 550-600 мс.
Div2C-Div1A
Почему неверно следующее:
не k+1 и k, а k+1 и k число Фибоначчи.
Что? Откуда тут числа Фибоначчи?
У меня k — кол-во шагов.
Это оптимальный вариант начала. У вас же получатся что-то либо неправильное(вроде бы), либо уж как минимум медленнее растущее.
если в какой то момент x==y (для натуральных)то дальше мы будем получать последовательность фибоначи домноженную на x
т.е по факту мы же так и генерирем пары .
из тройки x , y , x+y выбераем пару наибольших.
если зациклились то -1 иначе псевдо фибоначи ( т.е фибоначи с произвольной начальной парой)
Это называется не "произведение игр", а "сумма игр". Произведение игр — это когда каждый игрок одновременно делает ход во всех играх.
Точно, спасибо.
Поскольку я так и не посчитал кол-во ходов, то спрошу тут: такое решение ( 3896755 ) каким-то тестом валится или всегда заходит?
Пользуемся симметричностью таблицы и храним только первую четверть (но ходы делаем по одному, как описано в условии).
Что мешает посчитать количество итераций цикла while(ch) ?)
Да и очевидно, что если при n=30000 заходит с хорошим запасом, то ничем другим валиться не может.
Здравствуйте, сможет ли мне кто-то сказать 8-ой тест задачи B второго дивизиона ? Вроде сам делал как в разборе, не могу найти ошибку. Спасибо.
Все тесты уже доступны. Можно зайти в список попыток, нажать на номер той, которую хотите посмотреть. Там увидите исходный код, тесты прошедшие и где завалилось. Вот ваша последняя, например, — http://mirror.codeforces.com/contest/318/submission/3892064
Большое спасибо) ответ интовский взял а там ЛЛ ((( ужас...
Обсуждая с товарищем сегодняшнюю div1-D, я внезапно понял, что допустил досадный баг в прошедшем решении. Я ввёл константу SQ = 40000, и далее сначала шёл до SQ - 1, выделяя цепочки степеней чисел, и приксоривая соответствующие нимы, а потом одним махом учитывал все одноэлементные цепочки от SQ до N следующей строкой:
3891088
За get(1) здесь скрывается константа 1. То есть я просто брал и говорил, что от каждого числа на отрезке [SQ, N] добавится по единице в общий ксор. Что, естественно, неверно — некоторые числа участвуют в цепочках, учтённых нами ранее, и их добавлять ни в коем случае не нужно.
Я очень удивился тому, что такое решение прошло тесты. Казалось бы, если ксор первых SQ цепочек оказался равен 0 или 1, то ошибка в чётности количества единиц способна привести к неправильному ответу. То есть, на любом тесте, где, например, ответ — "Petya", потенциально моя программа может упасть, если ошибётся в чётности. Изменив константу на 40400 = 2012 - 1, я добился того, что она начала падать на куче тестов, где победителем был Петя. Завалить же решение с константой 40000 оказалось не так просто — оно на удивление часто... на удивление всегда угадывало чётность. Ну не магическая же, ради бога, константа, что в ней такого?
Я взял решение Romka, которое отличается от моего наличием счетчика учтенных чисел на отрезке [SQ, N], и начал стрессить. На случайных тестах, естественно, ничего не нашлось, потому что сгенерить случайный тест нулевым или единичным ксором почти невозможно. Родилась мысль в качестве N перебрать все степени целых чисел плюс-минус один на отрезке от 40000 до 109. И, о чудо, нашлось-таки некоторое количество тестов, которые валили мою программу.
Подобный баг всё-таки не сильно сложно допустить. А тестов, которые являются степенями целых чисел, стоило бы подобавлять. Вот такая история.
Макс, у меня в решении точно такой же баг. Только у меня вместо константы SQ было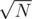 . И мое решение не прошло 46й тест. :(
. И мое решение не прошло 46й тест. :(
В 46м тесте N = 19000881 = 43592.
you can consider the case of (x,0) with maximum x. Apparently x<= log(4,n) . and general case (x',y') the x' s and y' s won't be larger than biggest x in (x,0)
That is not true. x can go upto 200 in fact, and 4^200 is much bigger than 20,000. The log4n bound doesnt hold because the 'distributed' ants can came back to the central axis, so its not always decreasing.
Can you illustrate how you were able to come to that bound of 200?
Honestly, during the contest, I coded the solution then ran it for 30,000, found the bound and then set it in the code. It wasn't 200, higher.
Is there mathematical approach to solve Div1B?
In "Ants" my simulation ends in 300ms, but 700ms is not enough for reading/writing. [edit: query counter used to be short] I rack a disciprine
In 317D - Game with Powers, it's there any non-math method to print the table q(s)?
Oh ,I think I solve it! Thanks for the helping of ydc!
Hi where can I find the English analysis?
You can change the language to English by click the flag at the top right of the current page..
Can someone please explain how to compute q(s) efficiently? Is it possible to compute within 1s (Total number of states is 10^9) ?
Yes, it is possible, because not all states are reachable. To be more precise, the number of reachable states is 711457. Also, hash table makes it possible to quickly process them. For example: 3898005
Finally a solution that calculates the MEX values.. Thank you very much!
sorry.. submit in russian..
I think problem ``balance'' admits an solution with less than 0.5*n*n steps.
We only need to consider the following case: All the vessels are connected with eactly n-1 roads, and are formed into a tree.
Then, we can first pick a leaf vessel and make it balance, and then reduce it to a problem with n-1 vessels which are still a tree.
For making a leaf balance, we can do it in no more than n-1 steps.
So total steps is no more than (n-1) + (n — 2) + .. 1, which is no more than half of n^2.
You're right.I implemented the same idea and it took AC and I think it is easier :)
OK, so I will bring this one once again...
I started writing that post going to ask you why simulation in B runs in a reasonable time. Actually, while writing that I proved that it runs in Θ(n2) :P
Firstly let's observe that ants won't get out of square with side , it's pretty easy to show, denote that side by k.
, it's pretty easy to show, denote that side by k.
Firstly let's prove that O(n2) is sufficient. Let f(x, y) = (k - |x|)2 + (k - |y|)2. One can easily see that sum of values of that functions summed over points with ants decreases after each operation. Moreover this sum takes only positive integer values and is equal to Θ(n2) at start, so we obtain an upper bound on number of moves.
Now let's prove that Θ(n2) is necessary. Consider a horizontal line y = c and ants above it and let S be the sum of distances from that line of ants above that line. One can easily see that this S doesn't change when we perform an operation strictly above or strictly under our line and increases by 1 when doing operation on that line, so we have to perforrm at least S operations on that line in whole process. One can see that for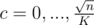 (K is some sufficiently large constant, let it be 10, playing with exact values is not needed here) we have
(K is some sufficiently large constant, let it be 10, playing with exact values is not needed here) we have 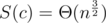 , so summing up we will obtain, that we have to perform at least Θ(n2) operations.
, so summing up we will obtain, that we have to perform at least Θ(n2) operations.
So, summing up, I don't think that setting n to 30000 was a good idea. Maybe it has a little constant, but some contestants won't be afraid of bounding the number of moves (as I proved, fully understandable anxiety!) and in result won't code that. I should also mention that solution may be more clever and won't perform operations one by one, if there are for example 100 ants in a cell at the moment, because we can perform 25 operations at once, but for now I can't estimate that thing.
can someone explain the bound of 200 in problem d- Ants