professorbrill's blog

Non-recursive DFS instead of recursive one
By professorbrill, 11 years ago, In English

It is a well-known task to answer whether a node is an ancestor to another one with time complexity O(n) for preprocessing and O(1) for a query.

Each time you enter the node in recursive function DFS, you increase the time counter by one and call it an "entrance" time, and after recursively processing its sons, you increase the time counter by one and call it an "exit" time. Here is the pseudocode.

DFS(u, p): // u is the current node, p is its parent
    increase the timer counter
    in[u] = timer
    for all (u, v) in edges:
        if v != p:
            DFS(v, u)
    increase the timer counter
    out[u] = timer

Now u is an ancestor of v .

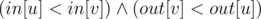Is there someway to implement the same algorithm but with non-recursive DFS?

  • Vote: I like it
  • +17
  • Vote: I do not like it

»
11 years ago, # |
← Rev. 4   Vote: I like it +17 Vote: I do not like it

Of course. You can mantain stack with pairs (vertex, flag), where flag = [in, out]. So, while stack not empty, you pick up pair from vertex. If it's "in" pair, you push (vertex, out) to stack and push childs (child_vertex, in) after. If it's "out" pair, you simply update out array.

Instead of pairs, you can mantain in/out information in array, cause first visit to vertex is always in and second visit is always out.

→ Reply