Тестовый раунд и его разбор были подготовлены snarknews и Gassa. Задачи тестового раунда уже использовались ранее в других соревнованиях. Все последующие раунды будут состоять из новых оригинальных задач, и вы все еще можете зарегистрироваться и поучаствовать в квалификационном раунде.

По ходу раунда многие участники пытались сдавать задачи «втёмную», время от времени даже выходя на первые строчки таблицы — правда, как оказалось после системных тестов, с одной фактически решённой задачей.

На момент окончания раунда первое место занимал tourist, сдавший все задачи, кроме B, «втёмную». Второе место занимал vepifanov, сдавший A, C и D «втёмную», а B и F — «в светлую» (причём каждую из них — с одной штрафной попыткой), третье — Anton_Lunyov, сдавший «втёмную» только задачу C. У остальных участников было сдано менее пяти задач. После системных тестов выяснилось, что у tourist было неверное решение по A, а у vepifanov — по D; тем самым, единственным участником, сдавшим 5 задач, стал Anton_Lunyov. У tourist — второе место, у vepifanov — третье.

Несколько странно, что задачи B и E (несмотря на не требующие особых знаний элементарные решения как в B, так и в E) остались в значительной степени «невостребованными»: все решившие эти задачи участники вошли в первую тройку, причём tourist решил E, а Anton_Lunyov и vepifanov — B.

Определённую сложность для участников, как оказалось, представляет работа со входными и выходными файлами: с этим было связано более 90% всех заданных жюри вопросов. Так что в последующих раундах Яндекс.Алгоритма файловый ввод-вывод решено не использовать.

Задача A (Окружности)

Данная задача является усложнённым вариантом задачи с нулевого («пилотного») Открытого Кубка, проходившего в мае 2004 года, или же упрощённым до двумерного случая вариантом задачи с Гран-При Москвы 2005 года.

Из формулы для площади треугольника S = abc / 4R получаем, что R = abc / 4S, где a, b и c — длины сторон треугольника. Учитывая, что координаты вершин целые, квадраты длин сторон являются целыми числами, равно как и удвоенная площадь треугольника, и можно вычислить R² точно, представив в виде отношения двух целых a²·b²·c² и 16S².

Так как координаты не превосходят 1400, то максимальное произведение сторон не превосходит 1400⁶·2, что меньше, чем 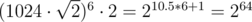, и вычисления можно производить в беззнаковых 64-битных целых. При этом при сравнении дробей потребуется или использовать встроенные типы для работы с длинными числами (в тех языках, в которых они есть), либо использовать модулярную арифметику, либо вычислять НОД, либо хранить старшую часть числа отдельно...

Отметим, что обычного double недостаточно даже без учёта погрешности вычислений: существует пример двух треугольников, радиусы описанных окружностей для которых различаются менее, чем на 2^- 52. Например, это треугольники с вершинами (0, 0), (1312, 164), (134, 1372) и (0, 0), (1351, 169), (106, 1317).

Вышеприведённый пример был построен при помощи следующего перебора: закрепляем одну вершину в начале координат, другие две — в точках (1400, 0) и (0, 1400), перебираем координаты этих двух точек в некоторой окрестности, вычисляя при этом радиусы описанных окружностей для всех треугольников, сортируем их и находим минимальную разность соседних радиусов после сортировки.

Как и ожидалось, по задаче было сделано много неудачных попыток, связанных с попыткой решения в double и последующим «поиском эпсилона» у большинства участников, которые сразу заметили возможность точного решения, реализация проблем не вызвала.

Задача B (Три дроби)

Эта задача впервые была предложена на Гран-При Москвы в 2005 году в более простой формулировке (без мультитеста).

Проще всего эту задачу решить предрасчётом.

Для заданных ограничений на n и количества запросов имеет смысл перед обработкой запросов построить полную таблицу ответов. Учитывая, что если n — составное число, и для всех простых чисел, меньших n, задача решена, то, представив n в виде произведения a·p, где p — простое, получаем решение 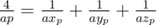. Таким образом, достаточно сначала предпросчётом построить таблицу для всех простых чисел и для n = 4, а затем вычислить вышеуказанным способом значения для остальных чисел.

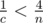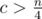Берём самую грубую оценку. Так как , то . Так как a > b > c, то 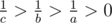, а значит 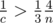, тем самым 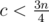; из аналогичных соображени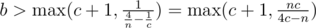й и 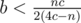. Соответственно, перебираем для всех простых n значения в указанных диапазонах и проверяем, делится ли nbc на 4bc - nb - nc нацело. Если делится, — требуемая тройка получена.

Построенный таким образом предрасчёт даже на очень медленном CoreDuo 1.6Ghz занимает менее минуты. В коде достаточно хранить только b и c, вычисляя оставшееся число по формуле 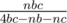. При этом размер кода не будет превосходить 50k, что меньше, чем source limit.

Кроме того, можно перебрать значения c и попытаться разложить разность в сумму двух «египетских» дробей, использовав алгоритм Фибоначчи; в этом случае решение укладывается в Time Limit без предрасчёта (именно такие решения и сдали оба участника, решивших задачу).

Эта задача представляет собой частный случай известной математической проблемы — гипотезы Эрдёша-Штрауса. В общем случае проблема на данный момент не решена, однако для всех n ≤ 10¹⁴ соответствующее разложение существует.

Для любителей конструктивных решений — несколько формул.

• Если n = 3k + 2, то получаем ,
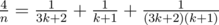• Если n = 4k, то получаем ,
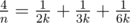• Если n = 4k + 2 и k > 1, то ,
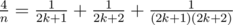• Если n = 4k + 3, то получаем ,
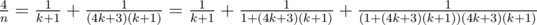• Если n = 8k + 5, то получаем .

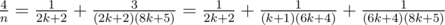То есть конструктивной формулы не существует только при n = 24k + 1.

Задача C (Выбери цифры)

Данная задача была впервые предложена на школьном кружке в Санкт-Петербургском ДТЮ в 2006 году.

Эта задача проста и допускает множество различных способов решения. Остановимся на некоторых из них. Далее мы считаем, что s — это заданная строка, а res — искомый результат.

Решение 1

Можно просто перебрать четвёрки позиций, которые мы выберем. Вот примерный код на языке Pascal:

res := 9999;
for i := 1 to 5 do
  for j := i + 1 to 6 do
    for k := j + 1 to 7 do
      for l := k + 1 to 8 do
        res := Min (res, StrToInt (s[i] + s[j] + s[k] + s[l]));

Решение 2

В языке высокого уровня могут найтись инструменты, которые сделают за нас всю черновую работу, связанную с перебором. Вот решение на языке Python, перебирающее все сочетания по четыре элемента:

res = "".join (min (itertools.combinations (s, 4)))

Решение 3

Перебор можно организовать рекурсивно. Вот функция на языке Java с двумя параметрами: позицией p в строке s и количеством цифр q, которые осталось взять. Она вызывается из основной программы как recur (8 - 1, 4) и идёт по позициям строки с конца.

int recur (int p, int q) {
  if (q < 0 || p + 1 < q) return 9999;
  if (p < 0) return 0;
  return Math.min (recur (p - 1, q),
    recur (p - 1, q - 1) * 10 + s.charAt (p) - '0');
}

Решение 4

Можно решать эту задачу методом динамического программирования. Два параметра — количество просмотренных позиций i и количество выбранных позиций j. Значение целевой функции f(i, j) — минимальное число, которое можно получить. Из каждого состояния можно пойти вперёд двумя способами: либо выбрать, либо пропустить текущую позицию, после чего переместиться на следующую позицию в строке. Ниже представлен код на языке C/C++. Ответ находится в ячейке таблицы f[8][4].

memset (f, 0x3F, sizeof (f));
f[0][0] = 0;
for (i = 0; i < 8; i++) {
  for (j = 0; j <= 4; j++) {
    f[i + 1][j] = min (f[i + 1][j], f[i][j]);
    f[i + 1][j + 1] = min (f[i + 1][j + 1],
      f[i][j] * 10 + (s[i] - '0'));
  }
}

Задача D (Различные сомножители)

Данная задача была впервые предложена на школьном кружке в Санкт-Петербургском ДТЮ в 2009 году.

Начнём разбор с теста, который имел номер 15: n = 112 500 = 2²·3²·5⁵. Его сложность заключается в том, что нельзя выбирать делитель 2·3 = 6: в противном случае всего делителей получится не больше шести. Вместо этого следует выбрать следующее разложение на семь сомножителей: 112 500 = 1·2·3·5·10·15·25.

Это минимальный тест, на котором не работают некоторые простые, но неправильные решения. Одно из таких решений — жадно выбирать делители, начиная с самых маленьких, пока после добавления очередного делителя d оставшееся число строго больше d. На этом тесте оно находит делители 1·2·3·5·6, и остаётся разложить на делители 625 = 5⁴, но ни 5, ни 25 = 5² взять нельзя.

Авторское решение — перебор. Тривиальный рекурсивный перебор делителей до корня в порядке возрастания успевает отработать менее чем за секунду. Следующая функция на языке C/C++, будучи запущена как recur (n, 1, 0), записывает в res количество делителей, а в массив best — сами делители. Параметры имеют следующий смысл: n — число, которое осталось разбить на множители, k — минимальный следующий делитель, а cur — количество уже выбранных делителей.

void recur (int n, int k, int cur) {
  if (res < cur + 1) {
    res = cur + 1;
    now[cur] = n;
    memmove (best, now, sizeof (best));
  }
  for (int d = k; d * (d + 1) <= n; d++)
    if (n % d == 0) {
      now[cur] = d;
      recur (n / d, d + 1, cur + 1);
    }
}

Как оценить, насколько быстро работает такой алгоритм? Можно заметить, что ответ не очень большой: поскольку произведение первых 13 натуральных чисел больше, чем 10⁹, ответ не превосходит 12. Это означает, что первый if сработает не более 12 раз. Также полезно знать, что у чисел, не превосходящих 10⁹, не более 1344 различных делителей (http://oeis.org/A066150).

Проще всего написать программу для грубой оценки, которая посчитает количество вызовов рекурсивной функции (язык C/C++). Здесь n — число, которое осталось разложить на множители, а k — минимально возможный следующий множитель.

int count (int n, int k) {
  int res = 0;
  for (int d = k; d * (d + 1) <= n; d++)
    res += 1 + count (n / d, d + 1);
  return res;
}

Эта программа отличается от нашего перебора тем, что в recur мы будем заходить внутрь рекурсии не на каждой итерации цикла по d, как в count, а только тогда, когда n делится нацело на d. Зато она позволяет нам использовать максимально возможное n для оценки (хоть и грубой) худшего случая, а не искать то большое число с большим количеством делителей, на котором реальная программа работает дольше всего.

При вызове count (1000000000, 1) результат равен 151 631 365. Если мы учтём, что единицу можно всегда взять отдельно и искать делители, начиная с двойки, то оценка сверху на количество делений будет равна результату count (1000000000, 2) — это число 75 815 682 (в два раза меньше). На самом же деле, поскольку корень из числа порядка 10⁹ имеет порядок 30 000, а делителей до корня не больше 1344 / 2 = 672, понятно, что делений будет в разы меньше. Максимальное число делений и/или взятий остатка от деления по всем тестам жюри оказалось равно 15 395 811.

Есть и более быстрые варианты перебора. Например, можно перебирать не все числа до корня, а только делители числа n, которые можно заранее найти за 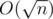. Можно также изначально разложить число n на простые множители и искать делители в виде наборов степеней для каждого из этих множителей.

Задача E (Таблица чемпионата)

Данная задача является адаптированным под memory limit=64 MiB вариантом задачи с Гран-При Москвы 2005 года. В первоначальной задаче ограничение по памяти было равно 3Mb, а длины названий команд не превышали 15 символов.

Существует два принципиально различных случая: когда все три утерянных числа относятся к одной команде и когда как минимум одно число относится к другой команде (или же утеряно меньше трёх чисел).

Обозначим количество матчей, сыгранных i-й командой, за P_i, количество побед — за W_i, количество ничьих — за D_i, количество поражений — за L_i и количество очков — за S_i.

Тогда верны следующие соотношения: W_i + D_i + L_i = P_i и 3W_i + D_i = S_i. В случае, если не все три утерянных числа относятся к одной команде, получаем, что надо решить несколько систем из двух линейных уравнений с не более чем двумя неизвестными.

В случае, если все три утерянных числа относятся к одной команде, третье уравнение получаем из того факта, что суммарное количество побед у всех команд равно суммарному количеству поражений, то есть W_i + W_- i = L_i + L_- i, где W_- i — суммарное количество побед у всех команд, кроме i-й, а L_- i — суммарное количество поражений у всех команд, кроме i-й.

Так что однозначное восстановление возможно всегда.

Основная проблема в данной задаче заключается в том, что таблица целиком в память не помещается.

Так что входной файл надо читать по строкам два раза: в первый раз — для того, чтобы построить соответствующую систему уравнений (при чтении суммируются W_i и L_i для составления системы во втором случае), во второй раз — чтобы найти содержащую ответ строку.

Задача F (Электротакси)

Данная задача была предложена польскими авторами и впервые была использована на первом этапе Всепольской школьной олимпиады по информатике сезона 2012-2013.

Очевидно, что или участок от таксопарка до точки назначения можно проехать без пересадок, или добраться до точки назначения невозможно (так как такси, которое доедет до точки назначения, обязано проехать участок от таксопарка до точки назначения полностью). Поэтому «зарезервируем» машину с минимальным запасом хода, которая может доехать от таксопарка до точки назначения, а также построим самую удалённую от точки назначения точку Z, из которой эта машина сможет забрать пассажира и доставить в точку назначения. Если таксопарк находится в точке назначения, то «резервирование» не производится.

Далее отсортируем «незарезервированные» машины по убыванию запаса хода и будем всякий раз выбирать машину с наибольшим запасом хода. Покажем, что этот алгоритм даёт как минимум не худшее решение по сравнению с каким-либо другим. Пусть сначала используется машина с запасом хода X₁, а затем — машина с запасом хода X₂, при этом пассажир изначально находится на расстояни a от таксопарка (и по другую сторону от точки назначения). Тогда пассажир проедет (X₁ - a) + (X₂ - (2a - X₁)) = 2X₁ + X₂ - 3a километров. Если X₂ > X₁, то, поменяв местами X₂ и X₁, увидим, что расстояние, которое проехал пассажир, увеличилось. Если машина с наибольшим запасом хода уже не может доехать (или «незарезервированные» машины закончились до того, как пассажир проехал точку Z), то добраться до точки назначения невозможно.

Если после очередного выбора пассажир оказался в точке Z или ближе к точке назначения, то он уже может доехать на отложенной машине. Также следует отдельно проверять случай, когда при выборе очередной машины пассажир сразу (без использования отложенной машины) может доехать до пункта назначения.