Hello, I'm trying to solve this problem Link. The problem statement is available in LiveArchive in English.
In the Brazilian SPOJ, the time-limit is quite strict, as the problem resumes to a grid shortest path, I choose the A* algorithm, which generally is faster than Djikstra and it's heuristics fits perfectly in 2-dimensional grids, but my solution isn't fast enough. How can I optimize more the A* ? The current code is:
struct MyLess {
bool operator () (int x, int y) {
return f[x] > f[y];
}
};
int func (void) {
int i, j;
dist[conv(RF,CF)] = 0;
vis[conv(RF,CF)] = 0;
priority_queue<int, vector<int>, MyLess> q;
q.push(conv(RF, CF));
for ( ; !q.empty(); ) {
int now = q.top(); q.pop();
if (vis[now]) {
continue;
}
vis[now] = 1;
if (now == conv(RT, CT)) return dist[now];
pair<int, int> od = rev(now);
for (i = 0; i < 24; i++) {
int ni = od.first + dx[i];
int nj = od.second + dy[i];
int next = conv(ni, nj);
if (ni <= 0 || nj <= 0 || ni > R || nj > C || graph[next] == 1 || vis[next]) continue;
if (next >= 0 && next < R * C) {
int next_cost = dist[now] + ct[i];
int heuristic = abs(ni - RT) + abs(nj - CT);
if (next_cost < dist[next]) {
dist[next] = next_cost;
f[next] = heuristic + next_cost;
q.push(next);
}
}
}
}
return dist[conv(RT,CT)];
}











Why this down votes ?
How do you calculate flooded areas?
What about that function?
How do you calculate flooded areas? I'm iterating over than all, it's rather bad O(N*M) for each flooded rectangle with sides N*M, but I think it's way more feasible than for each movement, check if it's position is valid O(W).
What about that function? In all material I've been reading about A* Algorithm, it stands that it's unique difference from Djikstra is the way it organizes the heap, instead of only check vertex with less distance, I should care about it's heuristics in relation to the goal vertex. I chooses Manhattan distance in relation to the goal vertex.
I didn't understood the idea behind your heuristic function, and why could it make it faster or better, could you explain that ?
H-m-m-m... I don't see A* here. What about not Dijkstra and not A*, but something BFS-like maintaining exactly 8 queues?
Before main cycle, 0-th queue contains start (the only cell), all other are empty. Main cycle looks like follows:
"Neighbors" are all cells marked on picture (totally 24 neighbors, or less when too near to border). "Still non-looked" should be implemented as in common BFS.
If standard STL queue seems to be not effective enough, you may implement it manually, less universal but more effective in particular case. But I believe STL queues may succeed too.
Hi, according to what I've read about A*, It's only a Dijkstra using the heuristic function to decide the ordering of the heap, actually I'm simply following the pseudo-code in Wikipedia.
Your idea is really clever, but I couldn't understand in what the usage of 8 queues different makes the search faster, the only idea I had is that It always take the elements from the shortest distance values ((i + 2) % 8, (i + 3) % 8 ... (i + 7) % 8)). Is this strategy that makes it fast ?
First of all, heap datastructure needs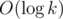 time for each push/pop operation (where k is current quantity of elements in heap). Using 8 usual (not priority) queues, it takes O(1) time.
time for each push/pop operation (where k is current quantity of elements in heap). Using 8 usual (not priority) queues, it takes O(1) time.
Another question, that (as far as I know) it's rather hard to choose such heuristic function in A*, that it really makes algorithm faster and never lead to inaccurate (rather near to minimal, but not exactly the minimal) answer.