Hi!
Solution Discussion for HHKB Programming Contest 2020
I created this blog, because I couldn't find an announcement in Codeforces (where usually there would be) and want to have a discussion about the solutions to the problems after the contest ended.
The contest is being held on Atcoder. Link to the problems in the contest: https://atcoder.jp/contests/hhkb2020/tasks.
Hope this will help people who didn't get a solution for problems.
Sorry for the bad English.











Summary for participant like noob like me : Solve ABC fast and take rest the remain time !!
How to solve D and E ???
A hint for E — For each tile, consider how many configurations will light it up
Do you mean calculating the number of tiles in each direction that will light up? Or did I made a mistake in understanding.
I mean, for a given tidy tile, I want to find out, in how many configurations this is lit up? For instance, in the second sample, there are 12 configurations that light up the top left of the grid (I'll leave it to you to figure out why). If you do that for every single tile on the grid and sum them up, you will get the answer.
how to solve E ?
For each tidy cell, find from how many tidy cells it can be lit. It can be lit up by continous line tidy cells in all 4 directions. Lets say the count of such cells is
litand total number of tidy cells istidy.Then that particular tidy cell, can be lit up in
2 ^ tidy - 2 ^ (tidy - lit)combinations.Submission
IDK why I got wrong answer in F. I derived the result using integration. Like for each continuous interval having bounds as discrete points, I do integral of V dP. Any ideas?
V : Value assumed by the maximum P : Probability function for that range for all the overlapping intervals
how did you found expectation, i was getting 117 as my answer for second sample. How should one calculate expectations in these type of problems??
I just noticed that in a bounded range, say for Value V, my change in probability function is contributed by the value that I just assumed.
How to solve D?
I used inclusion exclusion and combinatorics.
.
how to solve D?
How do you go about doing F? The way I tried is $$$P({x_1,x_2...} < z) = \prod \frac{z-l_i}{r_i-l_i}$$$ and the denominator removes the rightmost term of our answer. But the integration yields a polynomial I can't calculate (and I somehow have to handle that the probability maxes out at 1). If this is the right direction, how do you proceed from here?
To overcome this, I thought about fixing Li's but idk if this is right
Can you tell if this is true,
Expected value when there are N ranges, all having same range[L,R] is : L + (R-L)*(N/(N+1))
I think that's true if all assume same probability function?
Can we do it like this then ? (just assuming R_min >= L_max for ease)
sort all the pairs by R[i].
consider these N ranges now :
L_max to R[0] R[1] to R[2] R[2] to R[3] ... R[N-2] to R[N-1]
For each range, we find contribution of that range in the expected value, where we consider (N — i) i.i.d. RVs.
Yeah, I was doing the same thing, but got WA with it :(
Yes this is the right direction, I was not getting correct but to multiply this you need to do FFT(n*log^2(n)). This gives you a polynomial of the form
. Then you need to differentiate this, multiply by z and then integrate it in suitable range. I will try to get AC and then share the code. Hoping this helps.
so what should be the range of integration? min(Li) to max(Ri) ryt??
No, consider the ranges [1, 3] and [3, 5]. Note that [1, 3] is of no use.So here we use the range [3, 5] only. But now consider the ranges:[1, 4], [2, 6], [3, 9]. You can't simply consider the range [3, 9] since in [5, 9], the first range has no contribution. So you need to split between points:
and delete ranges which are of no use(division of polynomials).
Sort all L and R to find the "fundamental intervals" [fL, fR]. We'll assume the maximum is on each of these interval and calculate the expected values.
Fix an interval [fL, fR].
If fR <= L_i for some i, there's 0 probability that the max lies in the interval [fL, fR], so just skip.
Otherwise, let A_k be the probability that k of these variables lies in the interval [fL, fR]. The generating function
F(X)=A_0 + A_1 X + A_2 X^2...can be found by multiplying following polynomials for each variable i.If fL >= R_i, simply multiply the constant polynomial
1to the polynomial. Otherwise, multiply(fL - L_i) / (R_i - L_i) + (fR - fL) / (R_i - L_i) Xto the polynomial.After we've obtained the generating function, we can recover the answer using the fact that if we have N random variables with uniform distribution on [L, R], the expected maximum value is (L + R * N) / (N + 1).
Code
Thanks! I have some reading to do to understand how all this works
You don't need that fact. Let $$$P(x)$$$ be the probability of $$$x$$$. We need to find
This can be rewritten as
$P(<x)$ is the same. We have $$$\displaystyle\prod_{x \le R_i} \dfrac{x - L_i}{R_i - L_i}$$$. We know that the polynomial changes when $$$x = R_i$$$. Now we iterate in decreasing order of $$$R$$$, as in sort the ranges in decreasing order of $$$R$$$. Then we get
$$$\displaystyle\sum_{R_{i+1} \ge max(L_i)}\int_{R_{i+1}}^{R_i} 1 - \prod_{j \le i} \dfrac{x - L_j}{R_j - L_j}$$$. There is still some part missing, which is till $$$max(L)$$$. That can be added seperately, and we get $$$O(n^2)$$$.
I'm confused about the time complexity. It seems that it's $$$O(N^3)$$$?
It is, but it has the constant factor low enough to AC.
How to solve D? I tried to solving it by finding in how many cases squares will overlap and subtract that from
(n - a + 1) * (n - a + 1) * (n - b + 1) * (n - b + 1). But finding formula was too hard for me. :(same here.
when you get AC on E 5 sec after contest because your hands were shaking too much while submitting lol.
Can anyone share the approach for solving D and E.
for C, we can use DSU
source code
Ok, but a simple idea is to insert first 200005 numbers in a set and for each 'i', remove the element from the set and output the smallest element.
Or you can mark visited elements in a vector and increment the index until the next unvisited using the fact that the answer is always a non-decreasing sequence
for D, we use exclusive.
the total number can be easily given by
sqr(n-a+1) * sqr(n-b+1), then we subtract the number in three different overlapping cases.source code
Idea?
Can you please explain your approach?
for E, it's also exclusive
source code
Can you please use spoilers or links to show your code? Thanks!
i'm very sorry, because i'm in a hurry then.
No problem :)
m(at)ths(coder)
Can Anyone Share the Logic/Hint (Not the Code) to Approach D and E?
E was easier than D, at least to me. A quick explaination Let's try to find for each '.', in how many cases it will contribute.
We only need to know for a '.' , how many consecutive '.' are there to the left, right , up and down
We can also say, left+right and up+down information is also good enough, we don't want seperate left, right and so on. How do we find this information for each '.'
take two different 2-D arrays, one to store left-right info, other to store top-bottom. While you go from left to right, if current element is '.' then mark its value as , value of left + 1. If current is '#' mark it as 0.
For right most elements or element left to '#' we have correct information, but for rest, we need to do something.
One pass from right to left, if you are at '.' mark your value as max(Your value, value to your right). Wow !! Now we have useful information.
Repeat same for top-bottom. How to use the information we have stored ?
if total adjacents are x and total '.' are y, then the current cell will contribute in ?
((2^x) — 1)*(2^(y-x))
Take sum over all '.' . That's your answer
Here's one of the solution to D.
Let us find the number of ways such that there is no overlap in x-axis. Let us put A to the left and B to the right, such that on x-axis, now we have N-(A+B) blank space. Can you guess the number of ways to distribute these blank spaces between A and B ?
if P = N-(A+B), then we need to find number of integral solutions to a+b+c = P , a,b,c>=0 , where a is blank before A, b is blank between A and B and c is blank right to B.
Now that x-axis is covered, what about y-axis ?
A have (N-A+1) choices to set it's y-axis and B has (N-B+1).
We fixed left and right for A and B, but it can be other way too. So multiply above calculation with 2.
We can do a similar thing in Y-axis, and since everything remains same, we can multiply the above calculation with 2
Are we repeating any cases ?
Yes, Can you guess which are these cases ?
Where there is no overlap in x-axis and y-axis. How do we count these ?
We have actually done the hard work already, the cases are
solution to a+b+c = P for x-axis, and a+b+c = P in y-axis and to set A,B in left right up down states, we multiply it by 4.
Last up is, how to find number of integral solutions to a+b+c = n
it is standard, C(n+2,2)
To wrap up
Where there is no overlap in x-axis and y-axis.Can you please elaborate ? Thank you.Edit: I figured it out.
Could you please tell me how to sovle your problem ? thanks.
This might help...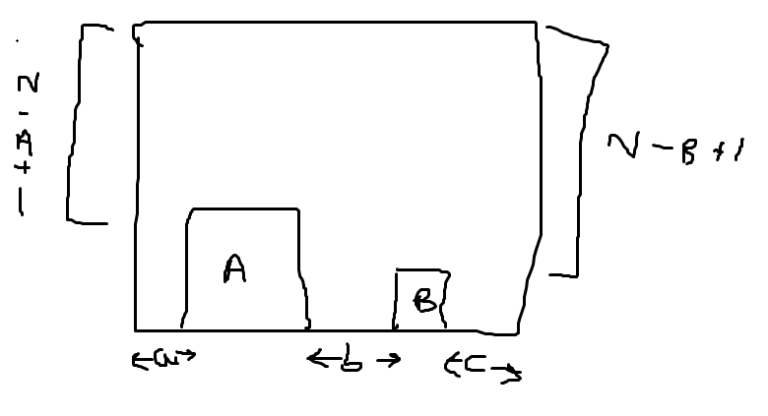
Now we multiply by 2 because we can flip the image and exchange the positions of A and B.
Now again multiply by 2 because we can rotate the image by 90 degrees for a new configuration.
Now there are cases when we are overcounting. Example: when A is on top right of B, now this is already counted again in a case when the image is rotated. So we need to subtract these kind of cases.
How to find those cases ? It is explained in the OP's comment.
Can you please explain what are we over counting and why is that the case? And how do we tackle it?
Thanks,i understand it!
go out to practice
Can someone please explain how to solve D?
Seems like a straight forward solution in which we subtract the overlapping cases. But how does it work, I am not able to wrap my head around it? Can someone please explain?
Submission link : https://atcoder.jp/contests/hhkb2020/submissions/17295052
Okay, I think I can explain... One thing to notice that if two square overlaps then there length and breadth of one rectangle must cross the breadth and length of the other rectangle so we need to discard those and we should count only the where the dimension don't overlap as mentioned i.e solution of the integral equation above which is shows the conditions of non-overlapping squares and subtract those which were counted twice due to rotations if u need further explanation u can ask
Thank you. I understand the integral equation above which calculates the conditions of non-overlapping squares. Can you please elaborate how do we calculate cases that were double counted (as in what to subtract) and how it works? (As in how do we account for repeating cases?)